

近年来,随着陆上风电机组装机厂址的扩展,在天气突变较多的地区安装的风力发电机组受到气象变化的影响愈发显著。在风况突变时,由于控制系统的滞后性,容易导致机组出现载荷过大,甚至是倒机的情况,造成重大经济损失。同时,现有超短期风功率预测的准确性较差,导致风功率预测系统对电网调度的参考价值不大,并且会导致业主产生大量的发电量计划考核。由于常见的激光雷达等风速测量产品单价高昂、受天气影响较大,难以实现批量化的应用部署,且在大时间空间尺度下仍难以具有可靠的前瞻性。因此,可靠的超短期风况预测迫在眉睫。
数据分析
训练集说明
5. 气象数据存储在 /训练集/[风场] 文件夹下。
测试集说明
1. 测试集分为两个文件夹:测试集初赛、测试集决赛,初赛和决赛的文件夹组织形式一致;
2. 初赛和决赛文件夹各包括80个时段的数据,每个时段1小时数据(30S分辨率,时间以秒数表达),春夏秋冬各20个时段,初赛编号1-20,决赛编号21-40;即初赛的时段编号为春_01-冬_20共80个;决赛的时段编号为春_21-冬_40共80个;
3. 各机组的数据文件按照 /测试集_**/[风场]/[机组]/[时段].csv 的方式存储;
4. 气象数据存储在 /测试集_**/[风场]/ 文件夹下,共80个时段风场所在地的风速风向数据,每个时段提供过去12小时和未来1小时的风速和风向数据。时段编码同上,时间编码为-11~2,其中0~1这个小时正好对应的是机舱的1小时数据。
缺失值
模型思路介绍
模型结构
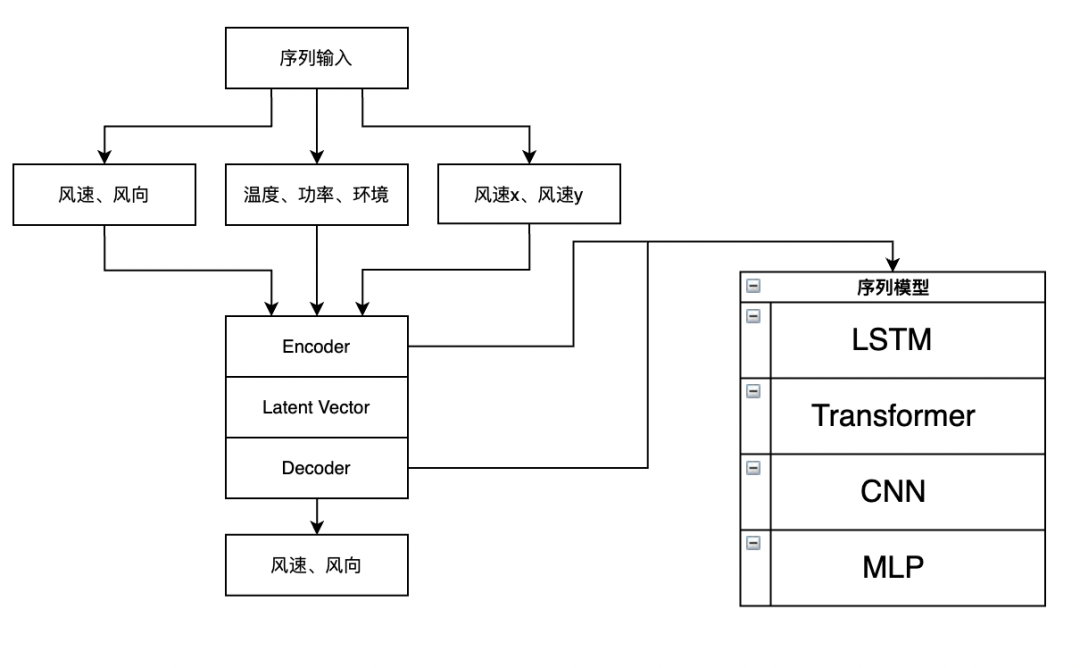
class network(nn.Layer):
def __init__(self, name_scope='baseline'):
super(network, self).__init__(name_scope)
name_scope = self.full_name()
self.lstm1 = paddle.nn.LSTM(128, 128, direction = 'bidirectional', dropout=0.0)
self.lstm2 = paddle.nn.LSTM(25, 128, direction = 'bidirectional', dropout=0.0)
self.embedding_layer1= paddle.nn.Embedding(100, 4)
self.embedding_layer2 = paddle.nn.Embedding(100, 16)
self.mlp1 = paddle.nn.Linear(29, 128)
self.mlp_bn1 = paddle.nn.BatchNorm(120)
self.bn2 = paddle.nn.BatchNorm(14)
self.mlp2 = paddle.nn.Linear(1536, 256)
self.mlp_bn2 = paddle.nn.BatchNorm(256)
self.lstm_out1 = paddle.nn.LSTM(256, 256, direction = 'bidirectional', dropout=0.0)
self.lstm_out2 = paddle.nn.LSTM(512, 128, direction = 'bidirectional', dropout=0.0)
self.lstm_out3 = paddle.nn.LSTM(256, 64, direction = 'bidirectional', dropout=0.0)
self.lstm_out4 = paddle.nn.LSTM(128, 64, direction = 'bidirectional', dropout=0.0)
self.output = paddle.nn.Linear(128, 2, )
self.sigmoid = paddle.nn.Sigmoid()
# 网络的前向计算函数
def forward(self, input1, input2):
embedded1 = self.embedding_layer1(paddle.cast(input1[:,:,0], dtype='int64'))
embedded2 = self.embedding_layer2(paddle.cast(input1[:,:,1]+input1[:,:,0] # * 30
, dtype='int64'))
x1 = paddle.concat([
embedded1,
embedded2,
input1[:,:,2:],
input1[:,:,-2:-1] * paddle.sin(np.pi * 2 *input1[:,:,-1:]),
input1[:,:,-2:-1] * paddle.cos(np.pi * 2 *input1[:,:,-1:]),
paddle.sin(np.pi * 2 *input1[:,:,-1:]),
paddle.cos(np.pi * 2 *input1[:,:,-1:]),
], axis=-1) # 4+16+5+2+2 = 29
x1 = self.mlp1(x1)
x1 = self.mlp_bn1(x1)
x1 = paddle.nn.ReLU()(x1)
x2 = paddle.concat([
embedded1[:,:14],
embedded2[:,:14],
input2[:,:,:-1],
input2[:,:,-2:-1] * paddle.sin(np.pi * 2 * input2[:,:,-1:]/360.),
input2[:,:,-2:-1] * paddle.cos(np.pi * 2 * input2[:,:,-1:]/360.),
paddle.sin(np.pi * 2 * input2[:,:,-1:]/360.),
paddle.cos(np.pi * 2 * input2[:,:,-1:]/360.),
], axis=-1) # 4+16+1+2+2 = 25
x2 = self.bn2(x2)
x1_lstm_out, (hidden, _) = self.lstm1(x1)
x1 = paddle.concat([
hidden[-2, :, :], hidden[-1, :, :],
paddle.max(x1_lstm_out, axis=1),
paddle.mean(x1_lstm_out, axis=1)
], axis=-1)
x2_lstm_out, (hidden, _) = self.lstm2(x2)
x2 = paddle.concat([
hidden[-2, :, :], hidden[-1, :, :],
paddle.max(x2_lstm_out, axis=1),
paddle.mean(x2_lstm_out, axis=1)
], axis=-1)
x = paddle.concat([x1, x2], axis=-1)
x = self.mlp2(x)
x = self.mlp_bn2(x)
x = paddle.nn.ReLU()(x)
# decoder
x = paddle.stack([x]*20, axis=1)
x = self.lstm_out1(x)[0]
x = self.lstm_out2(x)[0]
x = self.lstm_out3(x)[0]
x = self.lstm_out4(x)[0]
x = self.output(x)
output = self.sigmoid(x)*2-1
output = paddle.cast(output, dtype='float32')
return output
class TrainDataset(Dataset):
def __init__(self, x_train_array, x_train_array2, y_train_array=None, mode='train'):
# 样本数量
self.training_data = x_train_array.astype('float32')
self.training_data2 = x_train_array2.astype('float32')
self.mode = mode
if self.mode=='train':
self.training_label = y_train_array.astype('float32')
self.num_samples = self.training_data.shape[0]
def __getitem__(self, idx):
data = self.training_data[idx]
data2 = self.training_data2[idx]
if self.mode=='train':
label = self.training_label[idx]
return [data, data2], label
else:
return [data, data2]
def __len__(self):
# 返回样本总数量
return self.num_samples
model = paddle.Model(network(), inputs=inputs)
model.prepare(optimizer=paddle.optimizer.Adam(learning_rate=0.002,
parameters=model.parameters()),
loss=paddle.nn.L1Loss(),
)
model.fit(
train_data=train_loader,
eval_data=valid_loader,
epochs=10,
verbose=1,
)
优化pipeline
对于不同风机的数据,我们提取特征的方式是相同的,因此我们可以利用python的Parallel库进一步优化代码的性能,提升迭代的效率。核心代码如下:
# 生成训练数据
def generate_train_data(station, id):
df = read_data(station, id, 'train').values
return extract_train_data(df)
# 通过并行运算生成训练集合
train_data = []
for station in [1, 2]:
train_data_tmp = Parallel(n_jobs = -1, verbose = 1)(delayed(lambda x: generate_train_data(station, x))(id) for id in tqdm(range(25)))
train_data = train_data + train_data_tmp
拟合风向的问题
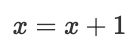 评价函数为 MAE。在训练阶段,直接预测风向会存在问题,因为0与1代表着相同的意义,模型在遇到风向为0/1的情况时预测为它们的均值0.5,导致误差。这里我们通过将
风向
、
角度
转化为
风向在垂直方向上的分量
,来避免直接预测风向,同时可以避免拟合风向带来的问题。
评价函数为 MAE。在训练阶段,直接预测风向会存在问题,因为0与1代表着相同的意义,模型在遇到风向为0/1的情况时预测为它们的均值0.5,导致误差。这里我们通过将
风向
、
角度
转化为
风向在垂直方向上的分量
,来避免直接预测风向,同时可以避免拟合风向带来的问题。
处理噪音
实验结果
比赛的分数由如下公式计算得出:
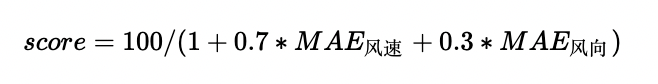
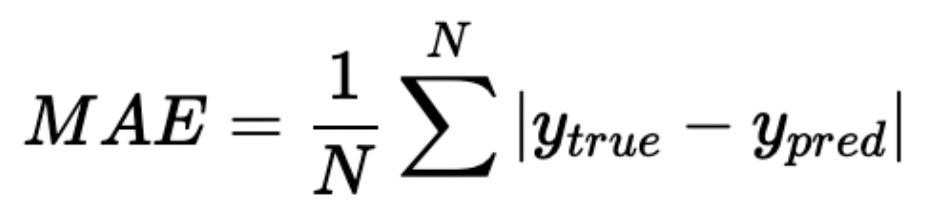 为平均绝对误差。实验结果如下表所示。不难发现,比赛成绩的提升主要来自于对数据与标签的处理,这也是我们在建模时最应该重视的两个要素。
为平均绝对误差。实验结果如下表所示。不难发现,比赛成绩的提升主要来自于对数据与标签的处理,这也是我们在建模时最应该重视的两个要素。

赛后感想
这一次工业大数据比赛中,我们在风况预测赛道与重型配件需求预测赛道中均取得了二等奖的好成绩。通过这一次比赛,我们发现工业场景下的数据质量可能并不理想,对缺失值、噪音都需要进行细心处理。在处理时间序列预测任务时,历史数据的积累中可能并不包括未来遇到的突发情况,仅仅依赖模型可能会存在较大的偏差,这也是我们在建模时需要格外关注的问题。
相关推荐

关注【飞桨PaddlePaddle】公众号
获取更多技术内容~