
常言道:遇事不决,量子力学,这虽然是一句玩笑话,但也说明了量子力学在社会中有很好的群众基础。随着科技的进步和科学的普及,基于量子力学和计算机科学交叉理论的量子计算开始逐渐出现在大家的视野中。通过成熟社交媒体的传播,像量子霸权(指量子计算在特定任务上大大超越传统计算机的速度,不过科学家们更倾向于使用量子优势这一说法)这样的词几乎做到了家喻户晓。
在这样的大背景下,百度飞桨也对这样的前沿技术领域进行了布局并在2020年推出了国内首个量子机器学习工具集——量桨(Paddle Quantum)。量子计算的原理究竟是什么?量子计算带来了哪些优势?量子机器学习又是什么新领域?
今天,我们一起通过量桨的官方入门手册结合作者的经验来学习量子计算,跟世界顶级科学家们迈入同一条赛道,这样想想还真有些小激动呢!
 图1 IBM公司制造的基于超导技术的量子计算机
图片来源:https://www.sciencenews.org/article/quantum-computers-are-about-get-real
图1 IBM公司制造的基于超导技术的量子计算机
图片来源:https://www.sciencenews.org/article/quantum-computers-are-about-get-real
圆柱形的容器绝大部分是稀释制冷机用于将置于容器最底层的量子处理器冷却至正常工作时候所需的极低温。
量子计算(Quantum Computing, QC)是一门量子力学与计算理论交叉形成的新型学科,本质上是通过量子力学的基本规律去操控信息单元量子比特(quantum bit, qubit)的新型计算模式。普遍认为这一概念是由著名物理学家费曼在1981年提出。量子比特与经典计算机中比特(bit)的概念很相似。经典逻辑比特只能处于0和1两种状态中的某一种,而量子比特可以处于两者的叠加态,换种说法,可以同时存储0和1。假设我们手头有一个量子比特的处理器,其可以同时处于个状态的叠加态。随着比特数的不断增大,这种信息存储能力将会是经典处理器遥不可及的。
另一方面,对量子比特的状态操控通常由一系列的量子逻辑门所构成的量子电路来描述。量子计算机的一次运算(执行一次量子电路)可以同时作用于存储器中的全部个状态,而这对于经典计算机来说则需要分别执行次操作。通过以上两点相信读者不难感受到量子计算机在原理上存在的优势。在接下来的部分,我们会进一步地谈谈量子比特和量子逻辑门并在量桨上完成量子计算中的“hello world”程序——制备和测量量子纠缠。想要系统性学习量子计算的读者建议进一步参阅量桨的官方入门手册和经典教材[1-2] 。
https://qml.baidu.com/quick-start/quantum-computing-fundamentals.html
在量子力学中,一个二能级系统微观粒子(qubit)的量子态(quantum state)可以表示为由两个正规正交基线性组合得到的向量。这些基向量一般可以写为:
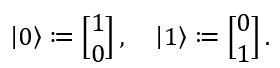
这里向量的表示方法采用了量子物理上传统的狄拉克表示(bra-ket)。这两个单位正交向量
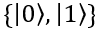 一般被称为“计算基”(computational basis)。一个单量子比特所处的任意量子态
一般被称为“计算基”(computational basis)。一个单量子比特所处的任意量子态
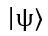 可以写成基向量
可以写成基向量
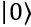 和
和
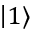 的线性叠加,也就是说,它可以被描述成一个
的线性叠加,也就是说,它可以被描述成一个
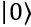 和
和
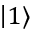 的线性组合:
的线性组合:
其中α和β是复数,他们表示概率振幅。根据波恩法则,当我们测量这个量子比特时,测量得到量子比特处于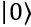 状态的概率是
状态的概率是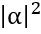 ;而测量得到
;而测量得到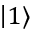 的概率是
的概率是
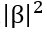 。由于概率相加等于1,因此有如下的限制条件:
。由于概率相加等于1,因此有如下的限制条件:
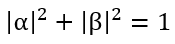 。
。
多量子比特系统也类似地由高维度的单位向量表示。比如说,一个两量子比特系统的状态可以被一个4维的复数向量表示,而这个复数空间的计算基是:
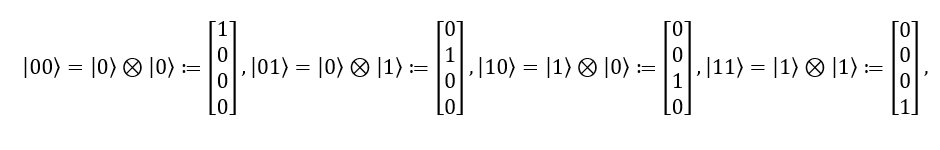
我们默认最左边的位置代表第一个量子比特。其中符号
 是张量积运算。工作原理如下:给定两个矩阵
是张量积运算。工作原理如下:给定两个矩阵
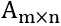 还有
还有
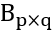 ,那么的张量积为:
,那么的张量积为:
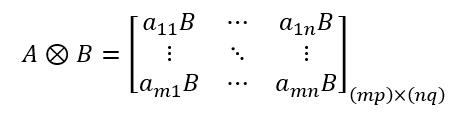
我们用一个球面上的点来表示一个量子比特可能处于的量子态,这个球面被称为布洛赫球面(Bloch Sphere),(见图2)
如果是一个经典比特的话,那么它只有两个状态0和1,也就是布洛赫球面的北极和南极。这两个位置恰好对应着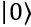 和
和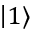 。而一个量子比特不光可以处于两极,它可以在球面上任意一点,这样一种叠加的状态是经典比特做不到的。举例来说,量子态
。而一个量子比特不光可以处于两极,它可以在球面上任意一点,这样一种叠加的状态是经典比特做不到的。举例来说,量子态
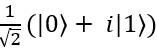 就处于球面赤道和y-正半轴的交界处。
就处于球面赤道和y-正半轴的交界处。
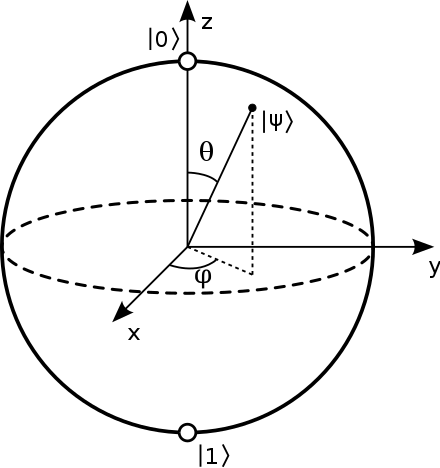
图2 单量子比特的布洛赫球面表示
在经典计算机中,我们可以在经典比特上施加基本的逻辑运算(非门 NOT、与非门 NAND、异或门 XOR、与门 AND、或门 OR)并组合成更复杂的运算。而量子计算有自己的一套逻辑运算,它们被称为量子门 (quantum gate)。经典计算机和量子计算机有不同的逻辑门构造,而量子算法是基于这些量子逻辑门的特殊性来设计的。量子门在数学上可以被表示成酉矩阵(unitary matrix)。
接下来,我们介绍在量子计算中非常重要的单量子比特门,包括泡利矩阵{X, Y, Z} 、单比特旋转门
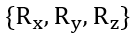 和哈达玛门 H(Hadamard)。其中非门(NOT gate)对于经典或量子计算都很重要,酉矩阵表示为:
和哈达玛门 H(Hadamard)。其中非门(NOT gate)对于经典或量子计算都很重要,酉矩阵表示为:
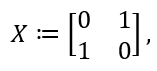
这个量子门(酉矩阵)作用在单量子比特(一个复向量)上本质上的运算是矩阵乘以向量。回忆起前面的布洛赫球面表示,这个矩阵X作用在一个量子比特(布洛赫球面上的一点)就相当于关于布洛赫球的x轴旋转角度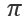 。这就是为什么可以表示成
。这就是为什么可以表示成
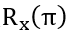 (相差全局相位
(相差全局相位
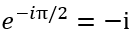 )。其它两个泡利矩阵Y和Z在这一点上也非常相似(代表绕y和z轴旋转角度
)。其它两个泡利矩阵Y和Z在这一点上也非常相似(代表绕y和z轴旋转角度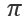 ):
):
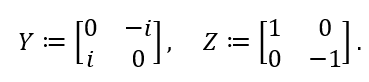
一般来说,任何一个在布洛赫球关于相应的轴旋转 θ角度的量子门可以表示为:
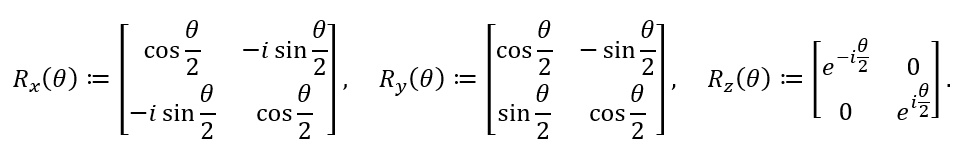
这些含有参数的旋转门是量子神经网络中的重要组成部分,我们会在下篇教程中介绍量子机器学习的相关概念时进行重点解释。
https://qml.baidu.com/api/paddle_quantum.circuit.uansatz.html
从单量子比特门我们可以拓展到两量子比特门。有两种拓展方式,第一种是只挑选出一个量子比特,在上面施加单量子比特门,其他的量子比特则不受影响。有的时候,你会见到如下图所示的量子电路:
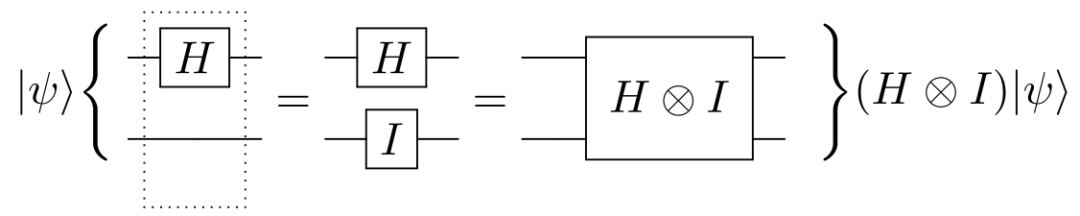
图3 两量子比特逻辑运算的电路表示和解读
作用在两量子比特上的量子门可以表示成一个4x4酉矩阵:
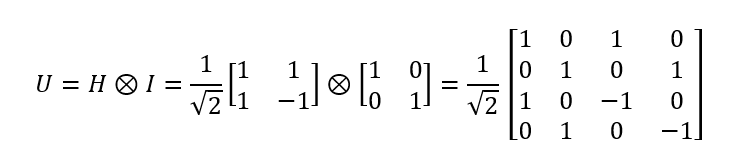
另一种拓展方式是将逻辑门直接作用在两个量子比特上。比如受控非门CNOT ,这个门会使得一个量子比特的状态影响到另一个量子比特的状态
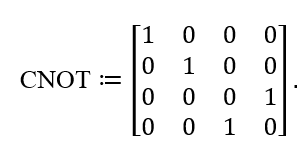
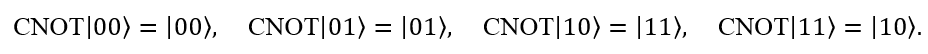
也就是说,当第一个量子比特处于
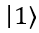 状态时, CNOT会在第二个量子比特上施加X门,如果第一个量子比特处于
状态时, CNOT会在第二个量子比特上施加X门,如果第一个量子比特处于
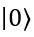 状态,那么第二个量子比特则不受任何影响。这也是为什么CNOT会被称为受控非门。
状态,那么第二个量子比特则不受任何影响。这也是为什么CNOT会被称为受控非门。
量桨(Paddle Quantum)
的使用介绍安装
用户可以直接通过 pip install paddle-quantum 完成安装。更详细的安装说明请参考量桨官方网站:
https://qml.baidu.com/install/installation_guide.html
量桨底层采用了自主研发的模拟器技术,波函数模式(state vector)下可以(用复数向量表示和储存量子态)在个人笔记本上支持20+量子比特的运算。在这种表示下,量子门(酉矩阵)作用在量子比特(一个复向量)上本质上的运算是矩阵乘以向量。代码中,具体体现在 cir.run_state_vector(input_state = None)。如果我们不输入任何初始量子态,就会默认所有的量子比特初始时都处于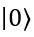 态。
https://qml.baidu.com/quick-start/operating-mode-of-paddle-quantum.html
态。
https://qml.baidu.com/quick-start/operating-mode-of-paddle-quantum.html
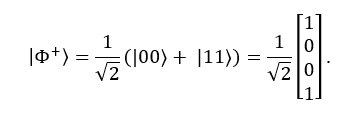
量子纠缠在量子通讯、量子计算以及其他量子技术中是一种很重要的资源。在量桨中,完成相应贝尔态的制备是很容易的。具体代码如下:
# 导入量子电路模块
from paddle_quantum.circuit import UAnsatz
# 初始化量子电路
cir = UAnsatz(2) # 2 表示使用两个量子比特
# 添加量子门
cir.h(0)
cir.cnot([0, 1])
# 制备输出态
# 如果用户不输入初始量子态,默认初始为|00..0>
output_state = cir.run_state_vector()
# 我们测量输出态2048次,获得测量结果频率分布
# 如果用户想获取概率分布的理论值,可以令 shots = 0
cir.measure(shots = 2048, plot = True)
print('我们制备出的贝尔态是:')
print(output_state.numpy())
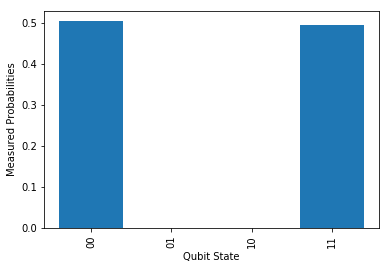
图4 制备出贝尔态的测量统计结果
[0.70710678+0.j 0.+0.j 0.+0.j 0.70710678+0.j]
本期主要讲了量子计算的基础知识介绍、量桨(Paddle Quantum)的使用介绍,下期我们将介绍量子机器学习以及具体的学习案例——变分量子本征求解器(VQE),敬请期待。让我们荡起双桨,在AI的海洋乘风破浪!因为水平有限,难免有不足之处,还请大家多多帮助。
https://quantum-hub.baidu.com/
[1] Nielsen, M. A. & Chuang, I. L. Quantum computation and quantum information. (Cambridge university press, 2010).
[2] Phillip Kaye, Laflamme, R. & Mosca, M. An Introduction to Quantum Computing. (2007).
如有飞桨相关技术有问题,欢迎在飞桨论坛中提问交流:
http://discuss.paddlepaddle.org.cn/
欢迎加入官方QQ群获取最新活动资讯:793866180。
如果您想详细了解更多飞桨的相关内容,请参阅以下文档。
https://www.paddlepaddle.org.cn/
GitHub: https://github.com/PaddlePaddle/Paddle
Gitee: https://gitee.com/paddlepaddle/Paddle
飞桨(PaddlePaddle)以百度多年的深度学习技术研究和业务应用为基础,集深度学习核心训练和推理框架、基础模型库、端到端开发套件和丰富的工具组件于一体,是中国首个自主研发、功能丰富、开源开放的产业级深度学习平台。飞桨企业版针对企业级需求增强了相应特性,包含零门槛AI开发平台EasyDL和全功能AI开发平台BML。EasyDL主要面向中小企业,提供零门槛、预置丰富网络和模型、便捷高效的开发平台;BML是为大型企业提供的功能全面、可灵活定制和被深度集成的开发平台。


 图1 IBM公司制造的基于超导技术的量子计算机
图1 IBM公司制造的基于超导技术的量子计算机
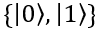 一般被称为“计算基”(computational basis)。一个单量子比特所处的任意量子态
一般被称为“计算基”(computational basis)。一个单量子比特所处的任意量子态
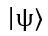 可以写成基向量
可以写成基向量
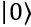 和
和
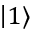 的线性叠加,也就是说,它可以被描述成一个
的线性叠加,也就是说,它可以被描述成一个
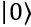 和
和
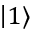 的线性组合:
的线性组合:
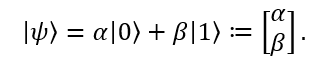
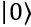 状态的概率是
状态的概率是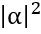 ;而测量得到
;而测量得到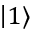 的概率是
的概率是
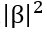 。由于概率相加等于1,因此有如下的限制条件:
。由于概率相加等于1,因此有如下的限制条件:
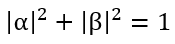 。
。
 是张量积运算。工作原理如下:给定两个矩阵
是张量积运算。工作原理如下:给定两个矩阵
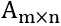 还有
还有
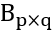 ,那么的张量积为:
,那么的张量积为:
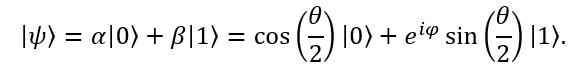
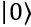 和
和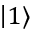 。而一个量子比特不光可以处于两极,它可以在球面上任意一点,这样一种叠加的状态是经典比特做不到的。举例来说,量子态
。而一个量子比特不光可以处于两极,它可以在球面上任意一点,这样一种叠加的状态是经典比特做不到的。举例来说,量子态
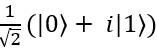 就处于球面赤道和y-正半轴的交界处。
就处于球面赤道和y-正半轴的交界处。
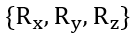 和哈达玛门 H(Hadamard)。其中非门(NOT gate)对于经典或量子计算都很重要,酉矩阵表示为:
和哈达玛门 H(Hadamard)。其中非门(NOT gate)对于经典或量子计算都很重要,酉矩阵表示为:
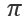 。这就是为什么可以表示成
。这就是为什么可以表示成
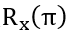 (相差全局相位
(相差全局相位
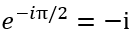 )。其它两个泡利矩阵Y和Z在这一点上也非常相似(代表绕y和z轴旋转角度
)。其它两个泡利矩阵Y和Z在这一点上也非常相似(代表绕y和z轴旋转角度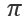 ):
):
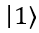 状态时, CNOT会在第二个量子比特上施加X门,如果第一个量子比特处于
状态时, CNOT会在第二个量子比特上施加X门,如果第一个量子比特处于
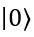 状态,那么第二个量子比特则不受任何影响。这也是为什么CNOT会被称为受控非门。
状态,那么第二个量子比特则不受任何影响。这也是为什么CNOT会被称为受控非门。
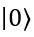 态。
态。

