MoE
通常来讲,模型规模的扩展会导致训练成本显著增加,计算资源的限制成为了大规模密集模型训练的瓶颈。为了解决这个问题, 《Outrageously large neural networks: The sparsely-gated mixture-of-experts layer》 提出了一种基于稀疏 MoE 层的深度学习模型架构,即将大模型拆分成多个小模型(专家, expert ), 每轮迭代根据样本决定激活一部分专家用于计算,达到了节省计算资源的效果; 并引入可训练并确保稀疏性的门( gate )机制,以保证计算能力的优化。
一、原理介绍
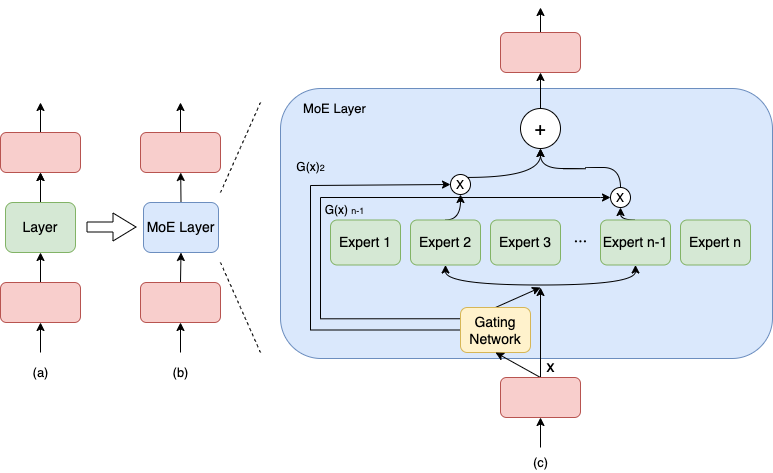
与密集模型不同,MoE 将模型的某一层扩展为多个具有相同结构的专家网络( expert ),并由门( gate )网络决定激活哪些 expert 用于计算,从而实现超大规模稀疏模型的训练。 以上图为例,示例模型包含 3 个模型层;如(a)到(b),将中间层扩展为具有 n 个 expert 的 MoE 结构,并引入 Gating network 和 Top_k 机制,MoE 细节见图(c),计算过程如下述公式。
上述第 1 个公式表示了包含 n 个专家的 MoE 层的计算过程。具体来讲,首先对样本 x 进行门控计算, W 表示权重矩阵;然后由 Softmax 处理后获得样本 x 被分配到各个 expert 的权重; 然后只取前 k (通常取 1 或者 2)个最大权重,最终整个 MoE Layer 的计算结果就是选中的 k 个专家网络输出的加权和。
二、功能效果
使用 MoE 结构,可以在计算成本次线性增加的同时实现超大规模模型训练,为恒定的计算资源预算带来巨大增益。
三、动态图使用方法
下面我们将分别介绍如何在动态图模式下使用飞桨框架进行 MoE 架构的适配和训练。以下代码(train_moe.py)在 Paddle2.3 以上可以运行,建议将 Paddle 版本升级到最新版.
首先导入需要的包
import paddle
from paddle.nn import Layer, LayerList, Linear, Dropout
from paddle.incubate.distributed.models.moe import MoELayer
from paddle.distributed.collective import Group
from paddle.distributed import fleet
import numpy as np
构建一个可以正常训练的模型
num_experts = 8
d_model = 512
d_hidden = 2048
class ExpertLayer(Layer):
def __init__(self, d_model, d_hidden, name=None):
super().__init__()
self.htoh4 = Linear(d_model, d_hidden)
self.h4toh = Linear(d_hidden, d_model)
def forward(self, x):
x = self.htoh4(x)
x = self.h4toh(x)
return x
然后初始化分布式环境,并构建 expert 通信组 moe_group
fleet.init(is_collective=True)
moe_group = paddle.distributed.new_group(list(range(fleet.worker_num())))
设置门网络的 gate 策略和 top_k 机制,并将模型单层扩展为 num_expert 个相同结构的专家网络
gate_config = {
"type": "gshard",
"top_k": 2,
}
experts_list = LayerList()
for expi in range(num_experts):
exp_layer = ExpertLayer(d_model, d_hidden)
experts_list.append(exp_layer)
接着调用 MoELayer API 封装并创建出 MoE 模型
class Model(Layer):
def __init__(self, d_model, d_hidden, name=None):
super().__init__()
self.linear1 = Linear(d_model, d_model)
self.moe_layer = MoELayer(d_model = d_model,
experts=experts_list,
gate=gate_config,
moe_group=moe_group,
recompute_interval=0)
self.linear2 = Linear(d_model, d_model)
self.dropout = Dropout(p=0.1)
def forward(self, x):
x = self.linear1(x)
x = self.moe_layer(x)
x = self.linear2(x)
x = self.dropout(x)
return x
model = Model(d_model, d_hidden)
optim = paddle.optimizer.SGD(parameters=model.parameters())
最后创建数据集,开始训练
for step in range(1, 100):
x = paddle.rand([4, 256, d_model])
y = model(x)
loss = y.mean()
loss.backward()
optim.step()
optim.clear_grad()
print("=== step : {}, loss : {}".format(step, loss.numpy()))
运行方式:
python -m paddle.distributed.launch --gpus=0,1,2,3,4,5,6,7 --log_dir logs train_moe.py