Variable
- class paddle.static. Variable ( block, type=<VarType.DENSE_TENSOR: 7>, name=None, shape=None, dtype=None, lod_level=None, capacity=None, persistable=None, error_clip=None, stop_gradient=False, is_data=False, need_check_feed=False, belong_to_optimizer=False, **kwargs ) [source]
-
Notes
The constructor of Variable should not be invoked directly.
In Static Graph Mode: Please use ** Block.create_var ** to create a Static variable which has no data until being feed.
In Dygraph Mode: Please use ** to_tensor ** to create a dygraph variable with real data.
In Fluid, every input and output of an OP is a variable. In most cases, variables are used for holding different kinds of data or training labels. A variable belongs to a api_guide_Block_en . All variable has its own name and two variables in different api_guide_Block_en could have the same name.
There are many kinds of variables. Each kind of them has its own attributes and usages. Please refer to the framework.proto for details.
Most of a Variable’s member variables can be set to be None. It mean it is not available or will be specified later.
Examples
In Static Graph Mode:
>>> import paddle.base as base >>> cur_program = base.Program() >>> cur_block = cur_program.current_block() >>> new_variable = cur_block.create_var(name="X", ... shape=[-1, 23, 48], ... dtype='float32')
In Dygraph Mode:
>>> import paddle.base as base >>> import numpy as np >>> import paddle >>> with base.dygraph.guard(): ... new_variable = paddle.to_tensor(np.arange(10))
-
detach
(
)
detach¶
-
Returns a new Variable, detached from the current graph. It will share data with origin Variable and without tensor copy. In addition, the detached Variable doesn’t provide gradient propagation.
- Returns
-
( api_guide_Variable_en | dtype is same as current Variable), The detached Variable.
Examples
>>> import paddle >>> paddle.enable_static() >>> # create a static Variable >>> x = paddle.static.data(name='x', shape=[3, 2, 1]) >>> # create a detached Variable >>> y = x.detach()
-
numpy
(
)
numpy¶
-
- Notes:
-
This API is ONLY available in Dygraph mode
Returns a numpy array shows the value of current api_guide_Variable_en
- Returns
-
The numpy value of current Variable.
- Return type
-
ndarray
- Returns type:
-
ndarray: dtype is same as current Variable
Examples
>>> import paddle >>> import paddle.base as base >>> from paddle.nn import Linear >>> import numpy as np >>> data = np.random.uniform(-1, 1, [30, 10, 32]).astype('float32') >>> with base.dygraph.guard(): ... linear = Linear(32, 64) ... data_tensor = paddle.to_tensor(data) ... x = linear(data_tensor) ... print(x.numpy())
-
backward
(
retain_graph=False
)
backward¶
-
- Notes:
-
This API is ONLY available in Dygraph mode
Run backward of current Graph which starts from current Tensor.
- Parameters
-
retain_graph (bool, optional) – If False, the graph used to compute grads will be freed. If you would like to add more ops to the built graph after calling this method(
backward), set the parameterretain_graphto True, then the grads will be retained. Thus, setting it to False is much more memory-efficient. Defaults to False. - Returns
-
None
- Return type
-
NoneType
Examples
>>> import numpy as np >>> import paddle >>> paddle.disable_static() >>> x = np.ones([2, 2], np.float32) >>> inputs = [] >>> for _ in range(10): ... tmp = paddle.to_tensor(x) ... # if we don't set tmp's stop_gradient as False then, all path to loss will has no gradient since ... # there is no one need gradient on it. ... tmp.stop_gradient=False ... inputs.append(tmp) >>> ret = paddle.add_n(inputs) >>> loss = paddle.sum(ret) >>> loss.backward()
-
gradient
(
)
gradient¶
-
- Notes:
-
This API is ONLY available in Dygraph mode
Get the Gradient of Current Variable
- Returns
-
if Variable’s type is DenseTensor, return numpy value of the gradient of current Variable, if Variable’s type is SelectedRows, return tuple of ndarray, first element of tuple is numpy value of the gradient of current Variable, second element of tuple is numpy value of the rows of current Variable.
- Return type
-
ndarray or tuple of ndarray
Examples
>>> import paddle >>> import paddle.base as base >>> import numpy as np >>> # example1: return ndarray >>> x = np.ones([2, 2], np.float32) >>> with base.dygraph.guard(): ... inputs2 = [] ... for _ in range(10): ... tmp = paddle.to_tensor(x) ... tmp.stop_gradient=False ... inputs2.append(tmp) ... ret2 = paddle.add_n(inputs2) ... loss2 = paddle.sum(ret2) ... loss2.retain_grads() ... loss2.backward() ... print(loss2.gradient()) >>> # example2: return tuple of ndarray >>> with base.dygraph.guard(): ... embedding = paddle.nn.Embedding( ... 20, ... 32, ... weight_attr='emb.w', ... sparse=True) ... x_data = np.arange(12).reshape(4, 3).astype('int64') ... x_data = x_data.reshape((-1, 3, 1)) ... x_tensor = paddle.to_tensor(x_data) ... out = embedding(x_tensor) ... out.backward() ... print(embedding.weight.gradient())
-
clear_gradient
(
)
clear_gradient¶
-
- Notes:
-
1. This API is ONLY available in Dygraph mode
2. Use it only Variable has gradient, normally we use this for Parameters since other temporal Variable will be deleted by Python’s GC
Clear (set to
0) the Gradient of Current VariableReturns: None
Examples
>>> import paddle >>> import paddle.base as base >>> import numpy as np >>> x = np.ones([2, 2], np.float32) >>> inputs2 = [] >>> for _ in range(10): >>> tmp = paddle.to_tensor(x) >>> tmp.stop_gradient=False >>> inputs2.append(tmp) >>> ret2 = paddle.add_n(inputs2) >>> loss2 = paddle.sum(ret2) >>> loss2.retain_grads() >>> loss2.backward() >>> print(loss2.gradient()) >>> loss2.clear_gradient() >>> print("After clear {}".format(loss2.gradient())) 1.0 After clear 0.0
-
to_string
(
throw_on_error,
with_details=False
)
to_string¶
-
Get debug string.
- Parameters
-
throw_on_error (bool) – True if raise an exception when self is not initialized.
with_details (bool) – more details about variables and parameters (e.g. trainable, optimize_attr, …) will be printed when with_details is True. Default value is False;
- Returns
-
The debug string.
- Return type
-
str
Examples
>>> >>> import paddle.base as base >>> import paddle >>> paddle.enable_static() >>> cur_program = base.Program() >>> cur_block = cur_program.current_block() >>> new_variable = cur_block.create_var(name="X", ... shape=[-1, 23, 48], ... dtype='float32') >>> print(new_variable.to_string(True)) >>> print("=============with detail===============") >>> print(new_variable.to_string(True, True)) name: "X" type { type: DENSE_TENSOR lod_tensor { tensor { data_type: FP32 dims: -1 dims: 23 dims: 48 } } } stop_gradient: false error_clip: None
-
element_size
(
)
element_size¶
-
Returns the size in bytes of an element in the Tensor.
Examples
>>> import paddle >>> paddle.enable_static() >>> x = paddle.static.data(name='x1', shape=[3, 2], dtype='bool') >>> print(x.element_size()) 1 >>> x = paddle.static.data(name='x2', shape=[3, 2], dtype='int16') >>> print(x.element_size()) 2 >>> x = paddle.static.data(name='x3', shape=[3, 2], dtype='float16') >>> print(x.element_size()) 2 >>> x = paddle.static.data(name='x4', shape=[3, 2], dtype='float32') >>> print(x.element_size()) 4 >>> x = paddle.static.data(name='x5', shape=[3, 2], dtype='float64') >>> print(x.element_size()) 8
- property stop_gradient
-
Indicating if we stop gradient from current Variable
Notes: This Property has default value as
Truein Dygraph mode, while Parameter’s default value is False. However, in Static Graph Mode all Variable’s default stop_gradient value isFalseExamples
>>> import paddle >>> import paddle.base as base >>> import numpy as np >>> with base.dygraph.guard(): ... value0 = np.arange(26).reshape(2, 13).astype("float32") ... value1 = np.arange(6).reshape(2, 3).astype("float32") ... value2 = np.arange(10).reshape(2, 5).astype("float32") ... linear = paddle.nn.Linear(13, 5) ... linear2 = paddle.nn.Linear(3, 3) ... a = paddle.to_tensor(value0) ... b = paddle.to_tensor(value1) ... c = paddle.to_tensor(value2) ... out1 = linear(a) ... out2 = linear2(b) ... out1.stop_gradient = True ... out = paddle.concat(x=[out1, out2, c], axis=1) ... out.backward() ... assert linear.weight.gradient() is None ... assert out1.gradient() is None
- property persistable
-
Indicating if we current Variable should be long-term alive
Notes: This Property will be deprecated and this API is just to help user understand concept
1. All Variable’s persistable is
Falseexcept Parameters.2. In Dygraph mode, this property should not be changed
Examples
>>> import paddle.base as base >>> cur_program = base.Program() >>> cur_block = cur_program.current_block() >>> new_variable = cur_block.create_var(name="X", ... shape=[-1, 23, 48], ... dtype='float32') >>> print("persistable of current Var is: {}".format(new_variable.persistable)) persistable of current Var is: False
- property is_parameter
-
Indicating if current Variable is a Parameter
Examples
>>> import paddle >>> paddle.enable_static() >>> new_parameter = paddle.static.create_parameter(name="X", ... shape=[10, 23, 48], ... dtype='float32') >>> if new_parameter.is_parameter: ... print("Current var is a Parameter") ... else: ... print("Current var is not a Parameter") Current var is a Parameter
- property grad_name
-
Indicating name of the gradient Variable of current Variable.
Notes: This is a read-only property. It simply returns name of gradient Variable from a naming convention but doesn’t guarantee the gradient exists.
Examples
>>> import paddle >>> paddle.enable_static() >>> x = paddle.static.data(name="x", shape=[-1, 23, 48], dtype='float32') >>> print(x.grad_name) x@GRAD
- property name
-
Indicating name of current Variable
Notes: If it has two or more Variable share the same name in the same api_guide_Block_en , it means these Variable will share content in no- Dygraph mode. This is how we achieve Parameter sharing
Examples
>>> import paddle.base as base >>> cur_program = base.Program() >>> cur_block = cur_program.current_block() >>> new_variable = cur_block.create_var(name="X", ... shape=[-1, 23, 48], ... dtype='float32') >>> print("name of current Var is: {}".format(new_variable.name)) name of current Var is: X
- property shape
-
Indicating shape of current Variable
Notes: This is a read-only property
Examples
>>> import paddle.base as base >>> cur_program = base.Program() >>> cur_block = cur_program.current_block() >>> new_variable = cur_block.create_var(name="X", ... shape=[-1, 23, 48], ... dtype='float32') >>> print("shape of current Var is: {}".format(new_variable.shape)) shape of current Var is: [-1, 23, 48]
- property dtype
-
Indicating data type of current Variable
Notes: This is a read-only property
Examples
>>> import paddle.base as base >>> cur_program = base.Program() >>> cur_block = cur_program.current_block() >>> new_variable = cur_block.create_var(name="X", ... shape=[-1, 23, 48], ... dtype='float32') >>> print("Dtype of current Var is: {}".format(new_variable.dtype)) Dtype of current Var is: paddle.float32
- property lod_level
-
Indicating
LoDinfo of current Variable, please refer to Tensor to check the meaning ofLoDNotes:
1. This is a read-only property
2. Don’t support this property in Dygraph mode, it’s value should be
0(int)Examples
>>> import paddle >>> import paddle.base as base >>> paddle.enable_static() >>> cur_program = base.Program() >>> cur_block = cur_program.current_block() >>> new_variable = cur_block.create_var(name="X", ... shape=[-1, 23, 48], ... dtype='float32') >>> print("LoD Level of current Var is: {}".format(new_variable.lod_level)) LoD Level of current Var is: 0
- property type
-
Indicating Type of current Variable
Notes: This is a read-only property
Examples
>>> >>> import paddle.base as base >>> cur_program = base.Program() >>> cur_block = cur_program.current_block() >>> new_variable = cur_block.create_var(name="X", ... shape=[-1, 23, 48], ... dtype='float32') >>> print("Type of current Var is: {}".format(new_variable.type)) Type of current Var is: VarType.DENSE_TENSOR
- property T
-
Permute current Variable with its dimensions reversed.
If n is the dimensions of x , x.T is equivalent to x.transpose([n-1, n-2, …, 0]).
Examples
>>> import paddle >>> paddle.enable_static() >>> x = paddle.ones(shape=[2, 3, 5]) >>> x_T = x.T >>> exe = paddle.static.Executor() >>> x_T_np = exe.run(paddle.static.default_main_program(), fetch_list=[x_T])[0] >>> print(x_T_np.shape) (5, 3, 2)
-
clone
(
)
clone¶
-
Returns a new static Variable, which is the clone of the original static Variable. It remains in the current graph, that is, the cloned Variable provides gradient propagation. Calling
out = tensor.clone()is same asout = assign(tensor).- Returns
-
Variable, The cloned Variable.
Examples
>>> import paddle >>> paddle.enable_static() >>> # create a static Variable >>> x = paddle.static.data(name='x', shape=[3, 2, 1]) >>> # create a cloned Variable >>> y = x.clone()
-
get_value
(
scope=None
)
get_value¶
-
Get the value of variable in given scope.
- Parameters
-
scope (Scope, optional) – If scope is None, it will be set to global scope obtained through ‘paddle.static.global_scope()’. Otherwise, use scope. Default: None
- Returns
-
Tensor, the value in given scope.
Examples
>>> import paddle >>> import paddle.static as static >>> import numpy as np >>> paddle.enable_static() >>> x = static.data(name="x", shape=[10, 10], dtype='float32') >>> y = static.nn.fc(x, 10, name='fc') >>> place = paddle.CPUPlace() >>> exe = static.Executor(place) >>> prog = paddle.static.default_main_program() >>> exe.run(static.default_startup_program()) >>> inputs = np.ones((10, 10), dtype='float32') >>> exe.run(prog, feed={'x': inputs}, fetch_list=[y, ]) >>> path = 'temp/tensor_' >>> for var in prog.list_vars(): ... if var.persistable: ... t = var.get_value() ... paddle.save(t, path+var.name+'.pdtensor') >>> for var in prog.list_vars(): ... if var.persistable: ... t_load = paddle.load(path+var.name+'.pdtensor') ... var.set_value(t_load)
-
set_value
(
value,
scope=None
)
set_value¶
-
Set the value to the tensor in given scope.
- Parameters
-
value (Tensor/ndarray) – The value to be set.
scope (Scope, optional) – If scope is None, it will be set to global scope obtained through ‘paddle.static.global_scope()’. Otherwise, use scope. Default: None
- Returns
-
None
Examples
>>> import paddle >>> import paddle.static as static >>> import numpy as np >>> paddle.enable_static() >>> x = static.data(name="x", shape=[10, 10], dtype='float32') >>> y = static.nn.fc(x, 10, name='fc') >>> place = paddle.CPUPlace() >>> exe = static.Executor(place) >>> prog = paddle.static.default_main_program() >>> exe.run(static.default_startup_program()) >>> inputs = np.ones((10, 10), dtype='float32') >>> exe.run(prog, feed={'x': inputs}, fetch_list=[y, ]) >>> path = 'temp/tensor_' >>> for var in prog.list_vars(): ... if var.persistable: ... t = var.get_value() ... paddle.save(t, path+var.name+'.pdtensor') >>> for var in prog.list_vars(): ... if var.persistable: ... t_load = paddle.load(path+var.name+'.pdtensor') ... var.set_value(t_load)
-
size
(
)
size¶
-
Returns the number of elements for current Variable, which is a int64 Variable with shape [] .
- Returns
-
Variable, the number of elements for current Variable
Examples
>>> import paddle >>> paddle.enable_static() >>> # create a static Variable >>> x = paddle.static.data(name='x', shape=[3, 2, 1]) >>> # get the number of elements of the Variable >>> y = x.size
- property attr_names
-
Get the names of all attributes defined.
-
attr
(
name
)
attr¶
-
Get the attribute by name.
- Parameters
-
name (str) – the attribute name.
- Returns
-
int|str|list, The attribute value. The return value can be any valid attribute type.
- property dist_attr
-
Get distributed attribute of this Variable.
-
abs
(
name: str | None = None
)
Tensor
abs¶
-
Perform elementwise abs for input x.
\[out = |x|\]- Parameters
-
x (Tensor) – The input Tensor with data type int32, int64, float16, float32, float64, complex64 and complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor.A Tensor with the same data type and shape as \(x\).
Examples
>>> import paddle >>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3]) >>> out = paddle.abs(x) >>> print(out) Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [0.40000001, 0.20000000, 0.10000000, 0.30000001])
-
abs_
(
name=None
)
abs_¶
-
Inplace version of
absAPI, the output Tensor will be inplaced with inputx. Please refer to abs.
-
acos
(
name: str | None = None
)
Tensor
acos¶
-
Acos Activation Operator.
\[out = cos^{-1}(x)\]- Parameters
-
x (Tensor) – Input of Acos operator, an N-D Tensor, with data type float32, float64, float16, bfloat16, uint8, int8, int16, int32, int64, complex64 or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
- Tensor. Output of Acos operator, a Tensor with shape same as input
-
(integer types are autocasted into float32).
Examples
>>> import paddle >>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3]) >>> out = paddle.acos(x) >>> print(out) Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [1.98231316, 1.77215421, 1.47062886, 1.26610363])
-
acos_
(
name=None
)
acos_¶
-
Inplace version of
acosAPI, the output Tensor will be inplaced with inputx. Please refer to acos.
-
acosh
(
name: str | None = None
)
Tensor
acosh¶
-
Acosh Activation Operator.
\[out = acosh(x)\]- Parameters
-
x (Tensor) – Input of Acosh operator, an N-D Tensor, with data type float32, float64, float16, bfloat16, uint8, int8, int16, int32, int64, complex64 or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
- Tensor. Output of Acosh operator, a Tensor with shape same as input
-
(integer types are autocasted into float32).
Examples
>>> import paddle >>> x = paddle.to_tensor([1., 3., 4., 5.]) >>> out = paddle.acosh(x) >>> print(out) Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [0. , 1.76274717, 2.06343699, 2.29243159])
-
acosh_
(
name=None
)
acosh_¶
-
Inplace version of
acoshAPI, the output Tensor will be inplaced with inputx. Please refer to acosh.
-
add
(
y: Tensor,
name: str | None = None,
*,
alpha: Number = 1,
out: Tensor | None = None
)
Tensor
add¶
-
Elementwise Add Operator. Add two tensors element-wise. The equation is:
\[Out=X+Y\]$X$ the tensor of any dimension. $Y$ the tensor whose dimensions must be less than or equal to the dimensions of $X$.
This operator is used in the following cases:
The shape of $Y$ is the same with $X$.
The shape of $Y$ is a continuous subsequence of $X$.
For example:
shape(X) = (2, 3, 4, 5), shape(Y) = (,) shape(X) = (2, 3, 4, 5), shape(Y) = (5,) shape(X) = (2, 3, 4, 5), shape(Y) = (4, 5), with axis=-1(default) or axis=2 shape(X) = (2, 3, 4, 5), shape(Y) = (3, 4), with axis=1 shape(X) = (2, 3, 4, 5), shape(Y) = (2), with axis=0 shape(X) = (2, 3, 4, 5), shape(Y) = (2, 1), with axis=0
Note
Alias Support: The parameter name
inputcan be used as an alias forx, andothercan be used as an alias fory. For example,add(input=tensor_x, other=tensor_y)is equivalent toadd(x=tensor_x, y=tensor_y).- Parameters
-
x (Tensor) – Tensor of any dimensions. Its dtype should be bool, bfloat16, float16, float32, float64, int8, int16, int32, int64, uint8, complex64, complex128. alias:
input.y (Tensor) – Tensor of any dimensions. Its dtype should be bool, bfloat16, float16, float32, float64, int8, int16, int32, int64, uint8, complex64, complex128. alias:
other.alpha (Number, optional) – Scaling factor for Y. Default: 1.
out (Tensor, optional) – The output tensor. Default: None.
name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Returns
-
N-D Tensor. A location into which the result is stored. It’s dimension equals with x.
Examples
>>> import paddle >>> x = paddle.to_tensor([2, 3, 4], 'float64') >>> y = paddle.to_tensor([1, 5, 2], 'float64') >>> z = paddle.add(x, y) >>> print(z) Tensor(shape=[3], dtype=float64, place=Place(cpu), stop_gradient=True, [3., 8., 6.])
-
add_
(
y: Tensor,
name: str | None = None,
*,
alpha: Number = 1
)
Tensor
add_¶
-
Inplace version of
addAPI, the output Tensor will be inplaced with inputx. Please refer to add.
-
add_n
(
name: str | None = None
)
Tensor
add_n¶
-
Sum one or more Tensor of the input.
For example:
Case 1: Input: input.shape = [2, 3] input = [[1, 2, 3], [4, 5, 6]] Output: output.shape = [2, 3] output = [[1, 2, 3], [4, 5, 6]] Case 2: Input: First input: input1.shape = [2, 3] Input1 = [[1, 2, 3], [4, 5, 6]] The second input: input2.shape = [2, 3] input2 = [[7, 8, 9], [10, 11, 12]] Output: output.shape = [2, 3] output = [[8, 10, 12], [14, 16, 18]]- Parameters
-
inputs (Tensor|list[Tensor]|tuple[Tensor]) – A Tensor or a list/tuple of Tensors. The shape and data type of the list/tuple elements should be consistent. Input can be multi-dimensional Tensor, and data types can be: bfloat16, float16, float32, float64, int32, int64, complex64, complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, the sum of input \(inputs\) , its shape and data types are consistent with \(inputs\).
Examples
>>> import paddle >>> input0 = paddle.to_tensor([[1, 2, 3], [4, 5, 6]], dtype='float32') >>> input1 = paddle.to_tensor([[7, 8, 9], [10, 11, 12]], dtype='float32') >>> output = paddle.add_n([input0, input1]) >>> output Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True, [[8. , 10., 12.], [14., 16., 18.]])
-
addmm
(
x: Tensor,
y: Tensor,
beta: float = 1.0,
alpha: float = 1.0,
name: str | None = None
)
Tensor
addmm¶
-
addmm
Perform matrix multiplication for input $x$ and $y$. $input$ is added to the final result. The equation is:
\[Out = alpha * x * y + beta * input\]$Input$, $x$ and $y$ can carry the LoD (Level of Details) information, or not. But the output only shares the LoD information with input $input$.
- Parameters
-
input (Tensor) – The input Tensor to be added to the final result.
x (Tensor) – The first input Tensor for matrix multiplication.
y (Tensor) – The second input Tensor for matrix multiplication.
beta (float, optional) – Coefficient of $input$, default is 1.
alpha (float, optional) – Coefficient of $x*y$, default is 1.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
The output Tensor of addmm.
- Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.ones([2, 2]) >>> y = paddle.ones([2, 2]) >>> input = paddle.ones([2, 2]) >>> out = paddle.addmm(input=input, x=x, y=y, beta=0.5, alpha=5.0) >>> print(out) Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True, [[10.50000000, 10.50000000], [10.50000000, 10.50000000]])
-
addmm_
(
x: Tensor,
y: Tensor,
beta: float = 1.0,
alpha: float = 1.0,
name: str | None = None
)
Tensor
addmm_¶
-
Inplace version of
addmmAPI, the output Tensor will be inplaced with inputinput. Please refer to addmm.
-
all
(
)
all¶
-
C++ interface function for all.
-
allclose
(
y: Tensor,
rtol: float = 1e-05,
atol: float = 1e-08,
equal_nan: bool = False,
name: str | None = None
)
Tensor
allclose¶
-
Check if all \(x\) and \(y\) satisfy the condition:
\[\left| x - y \right| \leq atol + rtol \times \left| y \right|\]elementwise, for all elements of \(x\) and \(y\). This is analogous to \(numpy.allclose\), namely that it returns \(True\) if two tensors are elementwise equal within a tolerance.
- Parameters
-
x (Tensor) – The input tensor, it’s data type should be float16, float32, float64.
y (Tensor) – The input tensor, it’s data type should be float16, float32, float64.
rtol (float, optional) – The relative tolerance. Default: \(1e-5\) .
atol (float, optional) – The absolute tolerance. Default: \(1e-8\) .
equal_nan (bool, optional) – ${equal_nan_comment}. Default: False.
name (str|None, optional) – Name for the operation. For more information, please refer to api_guide_Name. Default: None.
- Returns
-
The output tensor, it’s data type is bool.
- Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.to_tensor([10000., 1e-07]) >>> y = paddle.to_tensor([10000.1, 1e-08]) >>> result1 = paddle.allclose(x, y, rtol=1e-05, atol=1e-08, equal_nan=False, name="ignore_nan") >>> print(result1) Tensor(shape=[], dtype=bool, place=Place(cpu), stop_gradient=True, False) >>> result2 = paddle.allclose(x, y, rtol=1e-05, atol=1e-08, equal_nan=True, name="equal_nan") >>> print(result2) Tensor(shape=[], dtype=bool, place=Place(cpu), stop_gradient=True, False) >>> x = paddle.to_tensor([1.0, float('nan')]) >>> y = paddle.to_tensor([1.0, float('nan')]) >>> result1 = paddle.allclose(x, y, rtol=1e-05, atol=1e-08, equal_nan=False, name="ignore_nan") >>> print(result1) Tensor(shape=[], dtype=bool, place=Place(cpu), stop_gradient=True, False) >>> result2 = paddle.allclose(x, y, rtol=1e-05, atol=1e-08, equal_nan=True, name="equal_nan") >>> print(result2) Tensor(shape=[], dtype=bool, place=Place(cpu), stop_gradient=True, True)
-
amax
(
)
amax¶
-
C++ interface function for amax.
-
amin
(
)
amin¶
-
C++ interface function for amin.
-
angle
(
name: str | None = None
)
Tensor
angle¶
-
Element-wise angle of complex numbers. For non-negative real numbers, the angle is 0 while for negative real numbers, the angle is \(\pi\), and NaNs are propagated..
- Equation:
-
\[angle(x)=arctan2(x.imag, x.real)\]
- Parameters
-
x (Tensor) – An N-D Tensor, the data type is complex64, complex128, or float32, float64 .
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
An N-D Tensor of real data type with the same precision as that of x’s data type.
- Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.to_tensor([-2, -1, 0, 1]).unsqueeze(-1).astype('float32') >>> y = paddle.to_tensor([-2, -1, 0, 1]).astype('float32') >>> z = x + 1j * y >>> z Tensor(shape=[4, 4], dtype=complex64, place=Place(cpu), stop_gradient=True, [[(-2-2j), (-2-1j), (-2+0j), (-2+1j)], [(-1-2j), (-1-1j), (-1+0j), (-1+1j)], [-2j , -1j , 0j , 1j ], [ (1-2j), (1-1j), (1+0j), (1+1j)]]) >>> theta = paddle.angle(z) >>> theta Tensor(shape=[4, 4], dtype=float32, place=Place(cpu), stop_gradient=True, [[-2.35619450, -2.67794514, 3.14159274, 2.67794514], [-2.03444386, -2.35619450, 3.14159274, 2.35619450], [-1.57079637, -1.57079637, 0. , 1.57079637], [-1.10714877, -0.78539819, 0. , 0.78539819]])
-
any
(
)
any¶
-
C++ interface function for any.
-
append
(
var
)
append¶
-
Note
The type variable must be LoD Tensor Array.
-
argmax
(
axis: int | None = None,
keepdim: bool = False,
dtype: DTypeLike = 'int64',
name: str | None = None
)
Tensor
argmax¶
-
Computes the indices of the max elements of the input tensor’s element along the provided axis.
- Parameters
-
x (Tensor) – An input N-D Tensor with type float16, float32, float64, int16, int32, int64, uint8.
axis (int|None, optional) – Axis to compute indices along. The effective range is [-R, R), where R is x.ndim. when axis < 0, it works the same way as axis + R. Default is None, the input x will be into the flatten tensor, and selecting the min value index.
keepdim (bool, optional) – Whether to keep the given axis in output. If it is True, the dimensions will be same as input x and with size one in the axis. Otherwise the output dimensions is one fewer than x since the axis is squeezed. Default is False.
dtype (str|np.dtype, optional) – Data type of the output tensor which can be int32, int64. The default value is
int64, and it will return the int64 indices.name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Returns
-
Tensor, return the tensor of int32 if set
dtypeis int32, otherwise return the tensor of int64.
Examples
>>> import paddle >>> x = paddle.to_tensor([[5,8,9,5], ... [0,0,1,7], ... [6,9,2,4]]) >>> out1 = paddle.argmax(x) >>> print(out1.numpy()) 2 >>> out2 = paddle.argmax(x, axis=0) >>> print(out2.numpy()) [2 2 0 1] >>> out3 = paddle.argmax(x, axis=-1) >>> print(out3.numpy()) [2 3 1] >>> out4 = paddle.argmax(x, axis=0, keepdim=True) >>> print(out4.numpy()) [[2 2 0 1]]
-
argmin
(
axis: int | None = None,
keepdim: bool = False,
dtype: DTypeLike = 'int64',
name: str | None = None
)
Tensor
argmin¶
-
Computes the indices of the min elements of the input tensor’s element along the provided axis.
- Parameters
-
x (Tensor) – An input N-D Tensor with type float16, float32, float64, int16, int32, int64, uint8.
axis (int|None, optional) – Axis to compute indices along. The effective range is [-R, R), where R is x.ndim. when axis < 0, it works the same way as axis + R. Default is None, the input x will be into the flatten tensor, and selecting the min value index.
keepdim (bool, optional) – Whether to keep the given axis in output. If it is True, the dimensions will be same as input x and with size one in the axis. Otherwise the output dimensions is one fewer than x since the axis is squeezed. Default is False.
dtype (str|np.dtype, optional) – Data type of the output tensor which can be int32, int64. The default value is ‘int64’, and it will return the int64 indices.
name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Returns
-
Tensor, return the tensor of int32 if set
dtypeis int32, otherwise return the tensor of int64.
Examples
>>> import paddle >>> x = paddle.to_tensor([[5,8,9,5], ... [0,0,1,7], ... [6,9,2,4]]) >>> out1 = paddle.argmin(x) >>> print(out1.numpy()) 4 >>> out2 = paddle.argmin(x, axis=0) >>> print(out2.numpy()) [1 1 1 2] >>> out3 = paddle.argmin(x, axis=-1) >>> print(out3.numpy()) [0 0 2] >>> out4 = paddle.argmin(x, axis=0, keepdim=True) >>> print(out4.numpy()) [[1 1 1 2]]
-
argsort
(
axis: int = -1,
descending: bool = False,
stable: bool = False,
name: str | None = None
)
Tensor
argsort¶
-
Sorts the input along the given axis, and returns the corresponding index tensor for the sorted output values. The default sort algorithm is ascending, if you want the sort algorithm to be descending, you must set the
descendingas True.Note
Alias Support: The parameter name
inputcan be used as an alias forx, and the parameter namedimcan be used as an alias foraxis. For example,argsort(input=tensor_x, dim=1)is equivalent to(x=tensor_x, axis=1).- Parameters
-
x (Tensor) – An input N-D Tensor with type bfloat16, float16, float32, float64, int16, int32, int64, uint8. alias:
input.axis (int, optional) – Axis to compute indices along. The effective range is [-R, R), where R is Rank(x). when axis<0, it works the same way as axis+R. Default is -1. alias:
dim.descending (bool, optional) – Descending is a flag, if set to true, algorithm will sort by descending order, else sort by ascending order. Default is false.
stable (bool, optional) – Whether to use stable sorting algorithm or not. When using stable sorting algorithm, the order of equivalent elements will be preserved. Default is False.
name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Returns
-
Tensor, sorted indices(with the same shape as
xand with data type int64).
Examples
>>> import paddle >>> x = paddle.to_tensor([[[5,8,9,5], ... [0,0,1,7], ... [6,9,2,4]], ... [[5,2,4,2], ... [4,7,7,9], ... [1,7,0,6]]], ... dtype='float32') >>> out1 = paddle.argsort(x, axis=-1) >>> out2 = paddle.argsort(x, axis=0) >>> out3 = paddle.argsort(x, axis=1) >>> print(out1) Tensor(shape=[2, 3, 4], dtype=int64, place=Place(cpu), stop_gradient=True, [[[0, 3, 1, 2], [0, 1, 2, 3], [2, 3, 0, 1]], [[1, 3, 2, 0], [0, 1, 2, 3], [2, 0, 3, 1]]]) >>> print(out2) Tensor(shape=[2, 3, 4], dtype=int64, place=Place(cpu), stop_gradient=True, [[[0, 1, 1, 1], [0, 0, 0, 0], [1, 1, 1, 0]], [[1, 0, 0, 0], [1, 1, 1, 1], [0, 0, 0, 1]]]) >>> print(out3) Tensor(shape=[2, 3, 4], dtype=int64, place=Place(cpu), stop_gradient=True, [[[1, 1, 1, 2], [0, 0, 2, 0], [2, 2, 0, 1]], [[2, 0, 2, 0], [1, 1, 0, 2], [0, 2, 1, 1]]]) >>> x = paddle.to_tensor([1, 0]*40, dtype='float32') >>> out1 = paddle.argsort(x, stable=False) >>> out2 = paddle.argsort(x, stable=True) >>> print(out1) Tensor(shape=[80], dtype=int64, place=Place(cpu), stop_gradient=True, [55, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 1 , 57, 59, 61, 63, 65, 67, 69, 71, 73, 75, 77, 79, 17, 11, 13, 25, 7 , 3 , 27, 23, 19, 15, 5 , 21, 9 , 10, 64, 62, 68, 60, 58, 8 , 66, 14, 6 , 70, 72, 4 , 74, 76, 2 , 78, 0 , 20, 28, 26, 30, 32, 24, 34, 36, 22, 38, 40, 12, 42, 44, 18, 46, 48, 16, 50, 52, 54, 56]) >>> print(out2) Tensor(shape=[80], dtype=int64, place=Place(cpu), stop_gradient=True, [1 , 3 , 5 , 7 , 9 , 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59, 61, 63, 65, 67, 69, 71, 73, 75, 77, 79, 0 , 2 , 4 , 6 , 8 , 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78])
-
argwhere
(
)
Tensor
argwhere¶
-
Return a tensor containing the indices of all non-zero elements of the input tensor. The returned tensor has shape [z, n], where z is the number of all non-zero elements in the input tensor, and n is the number of dimensions in the input tensor.
- Parameters
-
input (Tensor) – The input tensor variable.
- Returns
-
Tensor, The data type is int64.
Examples
>>> import paddle >>> x = paddle.to_tensor([[1.0, 0.0, 0.0], ... [0.0, 2.0, 0.0], ... [0.0, 0.0, 3.0]]) >>> out = paddle.tensor.search.argwhere(x) >>> print(out) Tensor(shape=[3, 2], dtype=int64, place=Place(cpu), stop_gradient=True, [[0, 0], [1, 1], [2, 2]])
-
as_complex
(
name: str | None = None
)
Tensor
as_complex¶
-
Transform a real tensor to a complex tensor.
The data type of the input tensor is ‘float32’ or ‘float64’, and the data type of the returned tensor is ‘complex64’ or ‘complex128’, respectively.
The shape of the input tensor is
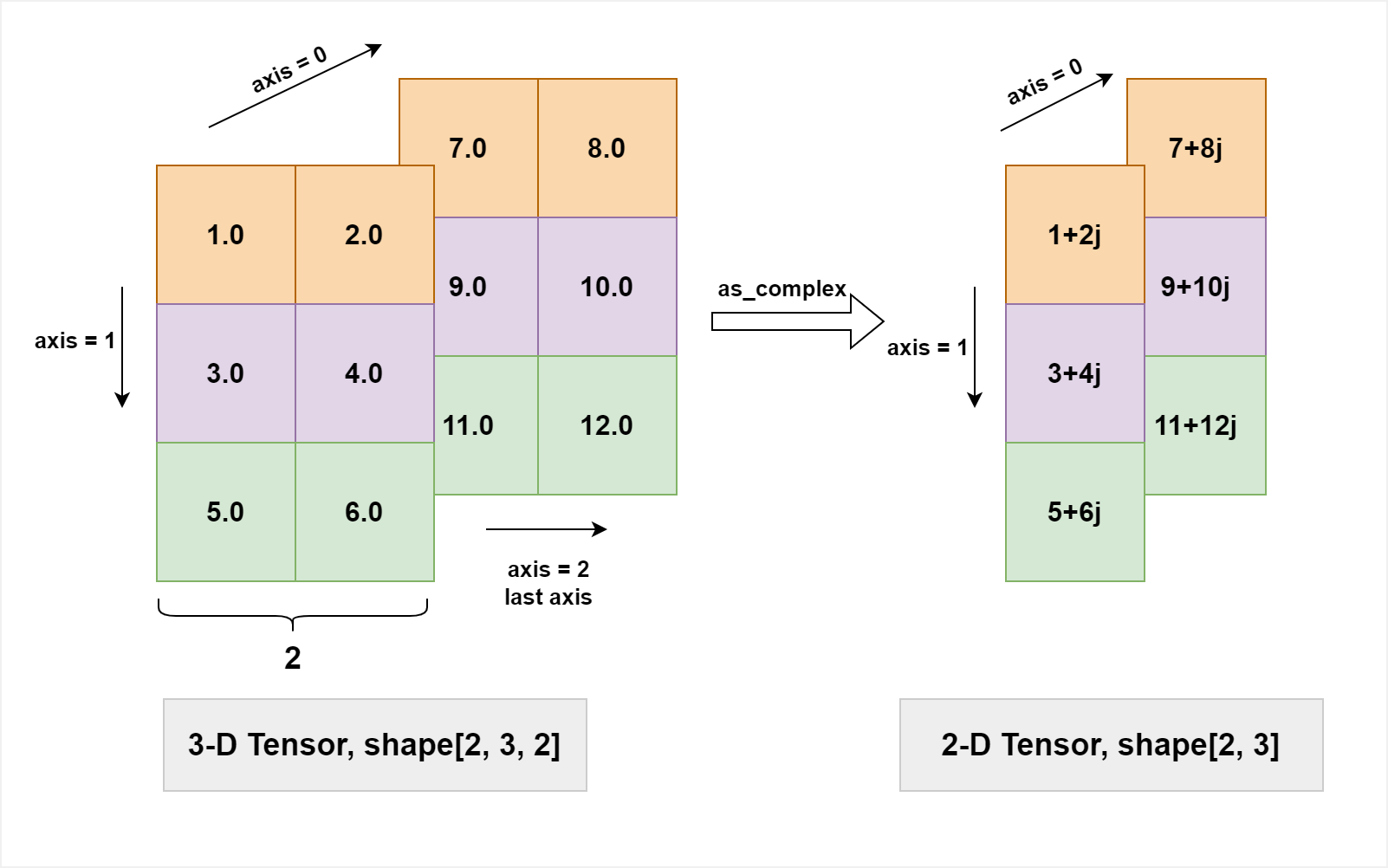
(* ,2), (*means arbitrary shape), i.e. the size of the last axis should be 2, which represent the real and imag part of a complex number. The shape of the returned tensor is(*,).The image below demonstrates the case that a real 3D-tensor with shape [2, 3, 2] is transformed into a complex 2D-tensor with shape [2, 3].
- Parameters
-
x (Tensor) – The input tensor. Data type is ‘float32’ or ‘float64’.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, The output. Data type is ‘complex64’ or ‘complex128’, with the same precision as the input.
Examples
>>> import paddle >>> x = paddle.arange(12, dtype=paddle.float32).reshape([2, 3, 2]) >>> y = paddle.as_complex(x) >>> print(y) Tensor(shape=[2, 3], dtype=complex64, place=Place(cpu), stop_gradient=True, [[1j , (2+3j) , (4+5j) ], [(6+7j) , (8+9j) , (10+11j)]])
-
as_real
(
name: str | None = None
)
Tensor
as_real¶
-
Transform a complex tensor to a real tensor.
The data type of the input tensor is ‘complex64’ or ‘complex128’, and the data type of the returned tensor is ‘float32’ or ‘float64’, respectively.
When the shape of the input tensor is
(*, ), (*means arbitrary shape), the shape of the output tensor is(*, 2), i.e. the shape of the output is the shape of the input appended by an extra2.- Parameters
-
x (Tensor) – The input tensor. Data type is ‘complex64’ or ‘complex128’.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, The output. Data type is ‘float32’ or ‘float64’, with the same precision as the input.
Examples
>>> import paddle >>> x = paddle.arange(12, dtype=paddle.float32).reshape([2, 3, 2]) >>> y = paddle.as_complex(x) >>> z = paddle.as_real(y) >>> print(z) Tensor(shape=[2, 3, 2], dtype=float32, place=Place(cpu), stop_gradient=True, [[[0. , 1. ], [2. , 3. ], [4. , 5. ]], [[6. , 7. ], [8. , 9. ], [10., 11.]]])
-
as_strided
(
shape: Sequence[int],
stride: Sequence[int],
offset: int = 0,
name: str | None = None
)
Tensor
as_strided¶
-
View x with specified shape, stride and offset.
Note that the output Tensor will share data with origin Tensor and doesn’t have a Tensor copy in
dygraphmode.The following image illustrates an example: transforming an input Tensor with shape [2,4,6] into a Tensor with
shape [8,6]andstride [6,1].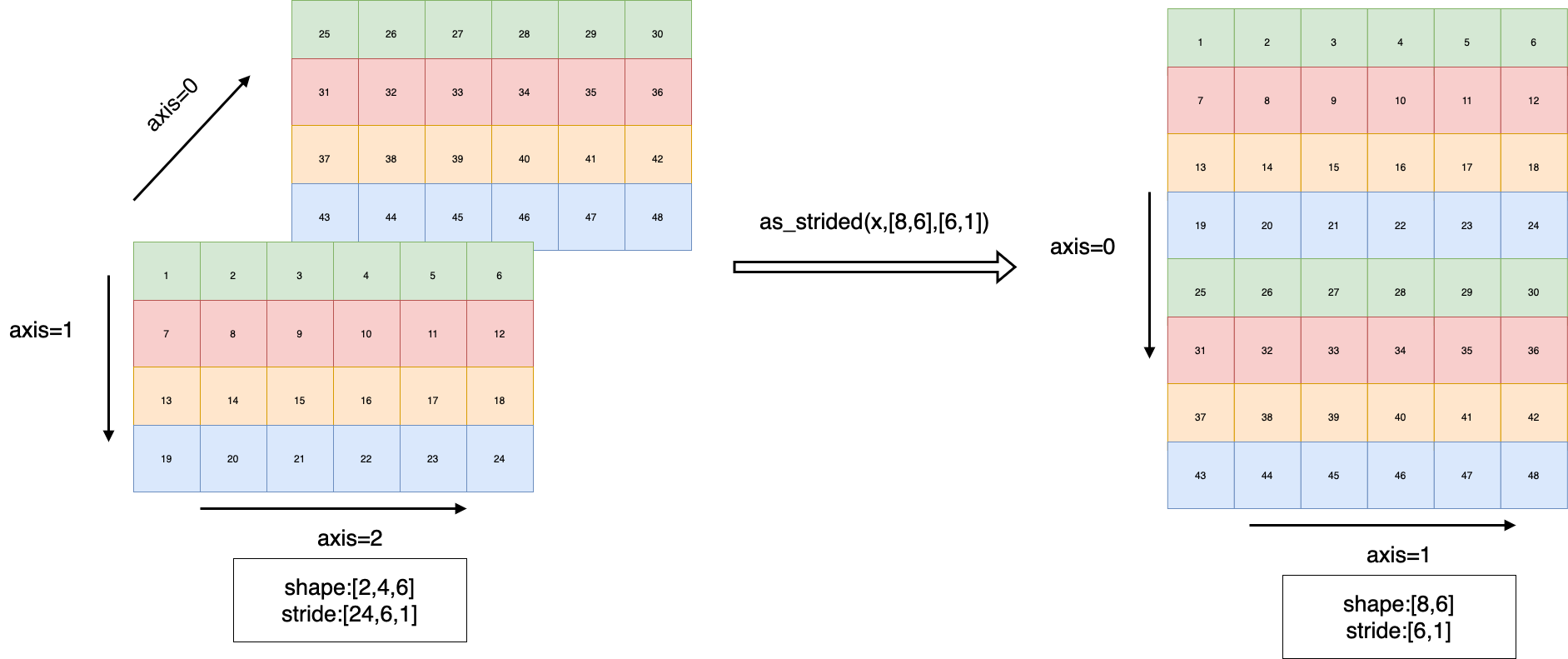
- Parameters
-
x (Tensor) – An N-D Tensor. The data type is
float32,float64,int32,int64orboolshape (list|tuple) – Define the target shape. Each element of it should be integer.
stride (list|tuple) – Define the target stride. Each element of it should be integer.
offset (int, optional) – Define the target Tensor’s offset from x’s holder. Default: 0.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, A as_strided Tensor with the same data type as
x.
Examples
>>> import paddle >>> paddle.base.set_flags({"FLAGS_use_stride_kernel": True}) >>> x = paddle.rand([2, 4, 6], dtype="float32") >>> out = paddle.as_strided(x, [8, 6], [6, 1]) >>> print(out.shape) [8, 6] >>> # the stride is [6, 1].
-
asin
(
name: str | None = None
)
Tensor
asin¶
-
Arcsine Operator.
\[out = sin^{-1}(x)\]- Parameters
-
x (Tensor) – Input of Asin operator, an N-D Tensor, with data type float32, float64, float16, bfloat16, uint8, int8, int16, int32, int64, complex64 or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
- Tensor. Same shape and dtype as input
-
(integer types are autocasted into float32).
Examples
>>> import paddle >>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3]) >>> out = paddle.asin(x) >>> print(out) Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [-0.41151685, -0.20135793, 0.10016742, 0.30469266])
-
asin_
(
name=None
)
asin_¶
-
Inplace version of
asinAPI, the output Tensor will be inplaced with inputx. Please refer to asin.
-
asinh
(
name: str | None = None
)
Tensor
asinh¶
-
Asinh Activation Operator.
\[out = asinh(x)\]- Parameters
-
x (Tensor) – Input of Asinh operator, an N-D Tensor, with data type float32, float64, float16, bfloat16, uint8, int8, int16, int32, int64, complex64 or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
- Tensor. Output of Asinh operator, a Tensor with shape same as input
-
(integer types are autocasted into float32).
Examples
>>> import paddle >>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3]) >>> out = paddle.asinh(x) >>> print(out) Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [-0.39003533, -0.19869010, 0.09983408, 0.29567307])
-
asinh_
(
name=None
)
asinh_¶
-
Inplace version of
asinhAPI, the output Tensor will be inplaced with inputx. Please refer to asinh.
-
astype
(
dtype
)
astype¶
-
- Notes:
-
The variable must be a Tensor
Cast a variable to a specified data type if it differs from the current dtype; otherwise, return the original variable.
- Parameters
-
self (Variable) – The source variable
dtype – The target data type
- Returns
-
Variable with new dtype
- Return type
-
Variable
Examples
In Static Graph Mode:
>>> import paddle >>> import paddle.base as base >>> paddle.enable_static() >>> startup_prog = paddle.static.Program() >>> main_prog = paddle.static.Program() >>> with base.program_guard(startup_prog, main_prog): ... original_variable = paddle.static.data(name = "new_variable", shape=[2,2], dtype='float32') ... new_variable = original_variable.astype('int64') ... print("new var's dtype is: {}".format(new_variable.dtype)) ... new var's dtype is: paddle.int64
In Dygraph Mode:
>>> import paddle.base as base >>> import paddle >>> import numpy as np >>> x = np.ones([2, 2], np.float32) >>> with base.dygraph.guard(): ... original_variable = paddle.to_tensor(x) ... print("original var's dtype is: {}, numpy dtype is {}".format(original_variable.dtype, original_variable.numpy().dtype)) ... new_variable = original_variable.astype('int64') ... print("new var's dtype is: {}, numpy dtype is {}".format(new_variable.dtype, new_variable.numpy().dtype)) ... original var's dtype is: paddle.float32, numpy dtype is float32 new var's dtype is: paddle.int64, numpy dtype is int64
-
atan
(
name: str | None = None
)
Tensor
atan¶
-
Arctangent Operator.
\[out = tan^{-1}(x)\]- Parameters
-
x (Tensor) – Input of Atan operator, an N-D Tensor, with data type float32, float64, float16, bfloat16, uint8, int8, int16, int32, int64, complex64 or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
- Tensor. Same shape and dtype as input x
-
(integer types are autocasted into float32).
Examples
>>> import paddle >>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3]) >>> out = paddle.atan(x) >>> print(out) Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [-0.38050640, -0.19739556, 0.09966865, 0.29145682])
-
atan2
(
y: Tensor,
name: str | None = None
)
Tensor
atan2¶
-
Element-wise arctangent of x/y with consideration of the quadrant.
- Equation:
-
\[\begin{split}atan2(x,y)=\left\{\begin{matrix} & tan^{-1}(\frac{x}{y}) & y > 0 \\ & tan^{-1}(\frac{x}{y}) + \pi & x>=0, y < 0 \\ & tan^{-1}(\frac{x}{y}) - \pi & x<0, y < 0 \\ & +\frac{\pi}{2} & x>0, y = 0 \\ & -\frac{\pi}{2} & x<0, y = 0 \\ &\text{undefined} & x=0, y = 0 \end{matrix}\right.\end{split}\]
- Parameters
-
x (Tensor) – An N-D Tensor, the data type is int32, int64, float16, float32, float64.
y (Tensor) – An N-D Tensor, must have the same type as x.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
An N-D Tensor, the shape and data type is the same with input (The output data type is float64 when the input data type is int).
- Return type
-
out (Tensor)
Examples
>>> import paddle >>> x = paddle.to_tensor([-1, +1, +1, -1]).astype('float32') >>> x Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [-1, 1, 1, -1]) >>> y = paddle.to_tensor([-1, -1, +1, +1]).astype('float32') >>> y Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [-1, -1, 1, 1]) >>> out = paddle.atan2(x, y) >>> out Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [-2.35619450, 2.35619450, 0.78539819, -0.78539819])
-
atan_
(
name=None
)
atan_¶
-
Inplace version of
atanAPI, the output Tensor will be inplaced with inputx. Please refer to atan.
-
atanh
(
name: str | None = None
)
Tensor
atanh¶
-
Atanh Activation Operator.
\[out = atanh(x)\]- Parameters
-
x (Tensor) – Input of Atan operator, an N-D Tensor, with data type float32, float64, float16, bfloat16, uint8, int8, int16, int32, int64, complex64 or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
- Tensor. Output of Atanh operator, a Tensor with shape same as input
-
(integer types are autocasted into float32).
Examples
>>> import paddle >>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3]) >>> out = paddle.atanh(x) >>> print(out) Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [-0.42364895, -0.20273255, 0.10033534, 0.30951962])
-
atanh_
(
name=None
)
atanh_¶
-
Inplace version of
atanhAPI, the output Tensor will be inplaced with inputx. Please refer to atanh.
-
atleast_1d
(
*,
name=None
)
atleast_1d¶
-
Convert inputs to tensors and return the view with at least 1-dimension. Scalar inputs are converted, one or high-dimensional inputs are preserved.
- Parameters
-
inputs (list[Tensor]) – One or more tensors. The data type is
float16,float32,float64,int16,int32,int64,int8,uint8,complex64,complex128,bfloat16orbool.name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
One Tensor, if there is only one input. List of Tensors, if there are more than one inputs.
Examples
>>> import paddle >>> # one input >>> x = paddle.to_tensor(123, dtype='int32') >>> out = paddle.atleast_1d(x) >>> print(out) Tensor(shape=[1], dtype=int32, place=Place(cpu), stop_gradient=True, [123]) >>> # more than one inputs >>> x = paddle.to_tensor(123, dtype='int32') >>> y = paddle.to_tensor([1.23], dtype='float32') >>> out = paddle.atleast_1d(x, y) >>> print(out) [Tensor(shape=[1], dtype=int32, place=Place(cpu), stop_gradient=True, [123]), Tensor(shape=[1], dtype=float32, place=Place(cpu), stop_gradient=True, [1.23000002])] >>> # more than 1-D input >>> x = paddle.to_tensor(123, dtype='int32') >>> y = paddle.to_tensor([[1.23]], dtype='float32') >>> out = paddle.atleast_1d(x, y) >>> print(out) [Tensor(shape=[1], dtype=int32, place=Place(cpu), stop_gradient=True, [123]), Tensor(shape=[1, 1], dtype=float32, place=Place(cpu), stop_gradient=True, [[1.23000002]])]
-
atleast_2d
(
*,
name=None
)
atleast_2d¶
-
Convert inputs to tensors and return the view with at least 2-dimension. Two or high-dimensional inputs are preserved.
The following diagram illustrates the behavior of atleast_2d on different dimensional inputs for the following cases:
A 0-dim tensor input.
A 0-dim tensor and a 1-dim tensor input.
A 0-dim tensor and a 3-dim tensor input.

In each case, the function returns the tensors (or a list of tensors) in views with at least 2 dimensions.
- Parameters
-
inputs (Tensor|list(Tensor)) – One or more tensors. The data type is
float16,float32,float64,int16,int32,int64,int8,uint8,complex64,complex128,bfloat16orbool.name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
One Tensor, if there is only one input. List of Tensors, if there are more than one inputs.
Examples
>>> import paddle >>> # one input >>> x = paddle.to_tensor(123, dtype='int32') >>> out = paddle.atleast_2d(x) >>> print(out) Tensor(shape=[1, 1], dtype=int32, place=Place(cpu), stop_gradient=True, [[123]]) >>> # more than one inputs >>> x = paddle.to_tensor(123, dtype='int32') >>> y = paddle.to_tensor([1.23], dtype='float32') >>> out = paddle.atleast_2d(x, y) >>> print(out) [Tensor(shape=[1, 1], dtype=int32, place=Place(cpu), stop_gradient=True, [[123]]), Tensor(shape=[1, 1], dtype=float32, place=Place(cpu), stop_gradient=True, [[1.23000002]])] >>> # more than 2-D input >>> x = paddle.to_tensor(123, dtype='int32') >>> y = paddle.to_tensor([[[1.23]]], dtype='float32') >>> out = paddle.atleast_2d(x, y) >>> print(out) [Tensor(shape=[1, 1], dtype=int32, place=Place(cpu), stop_gradient=True, [[123]]), Tensor(shape=[1, 1, 1], dtype=float32, place=Place(cpu), stop_gradient=True, [[[1.23000002]]])]
-
atleast_3d
(
*,
name=None
)
atleast_3d¶
-
Convert inputs to tensors and return the view with at least 3-dimension. Three or high-dimensional inputs are preserved.
- Parameters
-
inputs (Tensor|list(Tensor)) – One or more tensors. The data type is
float16,float32,float64,int16,int32,int64,int8,uint8,complex64,complex128,bfloat16orbool.name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
One Tensor, if there is only one input. List of Tensors, if there are more than one inputs.
Examples
>>> import paddle >>> # one input >>> x = paddle.to_tensor(123, dtype='int32') >>> out = paddle.atleast_3d(x) >>> print(out) Tensor(shape=[1, 1, 1], dtype=int32, place=Place(cpu), stop_gradient=True, [[[123]]]) >>> # more than one inputs >>> x = paddle.to_tensor(123, dtype='int32') >>> y = paddle.to_tensor([1.23], dtype='float32') >>> out = paddle.atleast_3d(x, y) >>> print(out) [Tensor(shape=[1, 1, 1], dtype=int32, place=Place(cpu), stop_gradient=True, [[[123]]]), Tensor(shape=[1, 1, 1], dtype=float32, place=Place(cpu), stop_gradient=True, [[[1.23000002]]])] >>> # more than 3-D input >>> x = paddle.to_tensor(123, dtype='int32') >>> y = paddle.to_tensor([[[[1.23]]]], dtype='float32') >>> out = paddle.atleast_3d(x, y) >>> print(out) [Tensor(shape=[1, 1, 1], dtype=int32, place=Place(cpu), stop_gradient=True, [[[123]]]), Tensor(shape=[1, 1, 1, 1], dtype=float32, place=Place(cpu), stop_gradient=True, [[[[1.23000002]]]])]
-
baddbmm
(
x: Tensor,
y: Tensor,
beta: float = 1.0,
alpha: float = 1.0,
name: str | None = None
)
Tensor
baddbmm¶
-
baddbmm
Perform batch matrix multiplication for input $x$ and $y$. $input$ is added to the final result. The equation is:
\[Out = alpha * x * y + beta * input\]$Input$, $x$ and $y$ can carry the LoD (Level of Details) information, or not. But the output only shares the LoD information with input $input$.
- Parameters
-
input (Tensor) – The input Tensor to be added to the final result.
x (Tensor) – The first input Tensor for batch matrix multiplication.
y (Tensor) – The second input Tensor for batch matrix multiplication.
beta (float, optional) – Coefficient of $input$, default is 1.
alpha (float, optional) – Coefficient of $x*y$, default is 1.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
The output Tensor of baddbmm.
- Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.ones([2, 2, 2]) >>> y = paddle.ones([2, 2, 2]) >>> input = paddle.ones([2, 2, 2]) >>> out = paddle.baddbmm(input=input, x=x, y=y, beta=0.5, alpha=5.0) >>> out Tensor(shape=[2, 2, 2], dtype=float32, place=Place(cpu), stop_gradient=True, [[[10.50000000, 10.50000000], [10.50000000, 10.50000000]], [[10.50000000, 10.50000000], [10.50000000, 10.50000000]]])
-
baddbmm_
(
x: Tensor,
y: Tensor,
beta: float = 1.0,
alpha: float = 1.0,
name: str | None = None
)
Tensor
baddbmm_¶
-
Inplace version of
baddbmmAPI, the output Tensor will be inplaced with inputinput. Please refer to baddbmm.
-
bernoulli_
(
p: float | Tensor = 0.5,
name: str | None = None
)
Tensor
bernoulli_¶
-
This is the inplace version of api
bernoulli, which returns a Tensor filled with random values sampled from a bernoulli distribution. The output Tensor will be inplaced with inputx. Please refer to bernoulli.- Parameters
-
x (Tensor) – The input tensor to be filled with random values.
p (float|Tensor, optional) – The success probability parameter of the output Tensor’s bernoulli distribution. If
pis float, all elements of the output Tensor shared the same success probability. Ifpis a Tensor, it has per-element success probabilities, and the shape should be broadcastable tox. Default is 0.5name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
- Returns
-
Tensor, A Tensor filled with random values sampled from the bernoulli distribution with success probability
p.
Examples
>>> import paddle >>> paddle.set_device('cpu') >>> paddle.seed(200) >>> x = paddle.randn([3, 4]) >>> x.bernoulli_() >>> print(x) Tensor(shape=[3, 4], dtype=float32, place=Place(cpu), stop_gradient=True, [[0., 1., 0., 1.], [1., 1., 0., 1.], [0., 1., 0., 0.]]) >>> x = paddle.randn([3, 4]) >>> p = paddle.randn([3, 1]) >>> x.bernoulli_(p) >>> print(x) Tensor(shape=[3, 4], dtype=float32, place=Place(cpu), stop_gradient=True, [[1., 1., 1., 1.], [0., 0., 0., 0.], [0., 0., 0., 0.]])
-
bincount
(
weights: Tensor | None = None,
minlength: int = 0,
name: str | None = None
)
Tensor
bincount¶
-
Computes frequency of each value in the input tensor.
- Parameters
-
x (Tensor) – A Tensor with non-negative integer. Should be 1-D tensor.
weights (Tensor, optional) – Weight for each value in the input tensor. Should have the same shape as input. Default is None.
minlength (int, optional) – Minimum number of bins. Should be non-negative integer. Default is 0.
name (str|None, optional) – Normally there is no need for user to set this property. For more information, please refer to api_guide_Name. Default is None.
- Returns
-
The tensor of frequency.
- Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.to_tensor([1, 2, 1, 4, 5]) >>> result1 = paddle.bincount(x) >>> print(result1) Tensor(shape=[6], dtype=int64, place=Place(cpu), stop_gradient=True, [0, 2, 1, 0, 1, 1]) >>> w = paddle.to_tensor([2.1, 0.4, 0.1, 0.5, 0.5]) >>> result2 = paddle.bincount(x, weights=w) >>> print(result2) Tensor(shape=[6], dtype=float32, place=Place(cpu), stop_gradient=True, [0. , 2.19999981, 0.40000001, 0. , 0.50000000, 0.50000000])
-
bitwise_and
(
y: Tensor,
out: Tensor | None = None,
name: str | None = None
)
Tensor
bitwise_and¶
-
Apply
bitwise_andon TensorXandY.\[Out = X \& Y\]Note
paddle.bitwise_andsupports broadcasting. If you want know more about broadcasting, please refer to please refer to Introduction to Tensor .- Parameters
-
x (Tensor) – Input Tensor of
bitwise_and. It is a N-D Tensor of bool, uint8, int8, int16, int32, int64.y (Tensor) – Input Tensor of
bitwise_and. It is a N-D Tensor of bool, uint8, int8, int16, int32, int64.out (Tensor|None, optional) – Result of
bitwise_and. It is a N-D Tensor with the same data type of input Tensor. Default: None.name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
- Returns
-
Result of
bitwise_and. It is a N-D Tensor with the same data type of input Tensor. - Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.to_tensor([-5, -1, 1]) >>> y = paddle.to_tensor([4, 2, -3]) >>> res = paddle.bitwise_and(x, y) >>> print(res) Tensor(shape=[3], dtype=int64, place=Place(cpu), stop_gradient=True, [0, 2, 1])
-
bitwise_and_
(
y: Tensor,
name: str | None = None
)
Tensor
bitwise_and_¶
-
Inplace version of
bitwise_andAPI, the output Tensor will be inplaced with inputx. Please refer to bitwise_and.
-
bitwise_invert
(
out: Tensor | None = None,
name: str | None = None
)
Tensor
bitwise_invert¶
-
Apply
bitwise_not(bitwise inversion) on Tensorx.This is an alias to the
paddle.bitwise_notfunction.\[Out = \sim X\]Note
paddle.bitwise_invertis functionally equivalent topaddle.bitwise_not.- Parameters
-
x (Tensor) – Input Tensor of
bitwise_invert. It is a N-D Tensor of bool, uint8, int8, int16, int32, int64.out (Tensor|None, optional) – Result of
bitwise_invert. It is a N-D Tensor with the same data type as the input Tensor. Default: None.name (str|None, optional) – The default value is None. This property is typically not set by the user. For more information, please refer to api_guide_Name.
- Returns
-
Result of
bitwise_invert. It is a N-D Tensor with the same data type as the input Tensor. - Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.to_tensor([-5, -1, 1]) >>> res = x.bitwise_invert() >>> print(res) Tensor(shape=[3], dtype=int64, place=Place(cpu), stop_gradient=True, [ 4, 0, -2])
-
bitwise_invert_
(
name: str | None = None
)
Tensor
bitwise_invert_¶
-
Inplace version of
bitwise_invertAPI, the output Tensor will be inplaced with inputx. Please refer to bitwise_invert_.
-
bitwise_left_shift
(
y: Tensor,
is_arithmetic: bool = True,
out: Tensor | None = None,
name: str | None = None
)
Tensor
bitwise_left_shift¶
-
Apply
bitwise_left_shifton TensorXandY.\[Out = X \ll Y\]Note
paddle.bitwise_left_shiftsupports broadcasting. If you want know more about broadcasting, please refer to please refer to Introduction to Tensor .- Parameters
-
x (Tensor) – Input Tensor of
bitwise_left_shift. It is a N-D Tensor of uint8, int8, int16, int32, int64.y (Tensor) – Input Tensor of
bitwise_left_shift. It is a N-D Tensor of uint8, int8, int16, int32, int64.is_arithmetic (bool, optional) – A boolean indicating whether to choose arithmetic shift, if False, means logic shift. Default True.
out (Tensor|None, optional) – Result of
bitwise_left_shift. It is a N-D Tensor with the same data type of input Tensor. Default: None.name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
- Returns
-
Result of
bitwise_left_shift. It is a N-D Tensor with the same data type of input Tensor. - Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.to_tensor([[1,2,4,8],[16,17,32,65]]) >>> y = paddle.to_tensor([[1,2,3,4,], [2,3,2,1]]) >>> paddle.bitwise_left_shift(x, y, is_arithmetic=True) Tensor(shape=[2, 4], dtype=int64, place=Place(gpu:0), stop_gradient=True, [[2 , 8 , 32 , 128], [64 , 136, 128, 130]])
>>> import paddle >>> x = paddle.to_tensor([[1,2,4,8],[16,17,32,65]]) >>> y = paddle.to_tensor([[1,2,3,4,], [2,3,2,1]]) >>> paddle.bitwise_left_shift(x, y, is_arithmetic=False) Tensor(shape=[2, 4], dtype=int64, place=Place(gpu:0), stop_gradient=True, [[2 , 8 , 32 , 128], [64 , 136, 128, 130]])
-
bitwise_left_shift_
(
y: Tensor,
is_arithmetic: bool = True,
out: Tensor | None = None,
name: str | None = None
)
Tensor
bitwise_left_shift_¶
-
Inplace version of
bitwise_left_shiftAPI, the output Tensor will be inplaced with inputx. Please refer to bitwise_left_shift.
-
bitwise_not
(
out: Tensor | None = None,
name: str | None = None
)
Tensor
bitwise_not¶
-
Apply
bitwise_noton TensorX.\[Out = \sim X\]Note
paddle.bitwise_notsupports broadcasting. If you want know more about broadcasting, please refer to please refer to Introduction to Tensor .- Parameters
-
x (Tensor) – Input Tensor of
bitwise_not. It is a N-D Tensor of bool, uint8, int8, int16, int32, int64.out (Tensor|None, optional) – Result of
bitwise_not. It is a N-D Tensor with the same data type of input Tensor. Default: None.name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
- Returns
-
Result of
bitwise_not. It is a N-D Tensor with the same data type of input Tensor. - Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.to_tensor([-5, -1, 1]) >>> res = paddle.bitwise_not(x) >>> print(res) Tensor(shape=[3], dtype=int64, place=Place(cpu), stop_gradient=True, [ 4, 0, -2])
-
bitwise_not_
(
name: str | None = None
)
Tensor
bitwise_not_¶
-
Inplace version of
bitwise_notAPI, the output Tensor will be inplaced with inputx. Please refer to bitwise_not.
-
bitwise_or
(
y: Tensor,
out: Tensor | None = None,
name: str | None = None
)
Tensor
bitwise_or¶
-
Apply
bitwise_oron TensorXandY.\[Out = X | Y\]Note
paddle.bitwise_orsupports broadcasting. If you want know more about broadcasting, please refer to please refer to Introduction to Tensor .Note
Alias Support: The parameter name
inputcan be used as an alias forx, andothercan be used as an alias fory. For example,bitwise_or(input=tensor_x, other=tensor_y, ...)is equivalent tobitwise_or(x=tensor_x, y=tensor_y, ...).- Parameters
-
x (Tensor) – Input Tensor of
bitwise_or. It is a N-D Tensor of bool, uint8, int8, int16, int32, int64. alias:input.y (Tensor) – Input Tensor of
bitwise_or. It is a N-D Tensor of bool, uint8, int8, int16, int32, int64. alias:oth.out (Tensor|None, optional) – Result of
bitwise_or. It is a N-D Tensor with the same data type of input Tensor. Default: None.name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
- Returns
-
Result of
bitwise_or. It is a N-D Tensor with the same data type of input Tensor. - Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.to_tensor([-5, -1, 1]) >>> y = paddle.to_tensor([4, 2, -3]) >>> res = paddle.bitwise_or(x, y) >>> print(res) Tensor(shape=[3], dtype=int64, place=Place(cpu), stop_gradient=True, [-1, -1, -3])
-
bitwise_or_
(
y: Tensor,
name: str | None = None
)
Tensor
bitwise_or_¶
-
Inplace version of
bitwise_orAPI, the output Tensor will be inplaced with inputx. Please refer to bitwise_or.
-
bitwise_right_shift
(
y: Tensor,
is_arithmetic: bool = True,
out: Tensor | None = None,
name: str | None = None
)
Tensor
bitwise_right_shift¶
-
Apply
bitwise_right_shifton TensorXandY.\[Out = X \gg Y\]Note
paddle.bitwise_right_shiftsupports broadcasting. If you want know more about broadcasting, please refer to please refer to Introduction to Tensor .- Parameters
-
x (Tensor) – Input Tensor of
bitwise_right_shift. It is a N-D Tensor of uint8, int8, int16, int32, int64.y (Tensor) – Input Tensor of
bitwise_right_shift. It is a N-D Tensor of uint8, int8, int16, int32, int64.is_arithmetic (bool, optional) – A boolean indicating whether to choose arithmetic shift, if False, means logic shift. Default True.
out (Tensor|None, optional) – Result of
bitwise_right_shift. It is a N-D Tensor with the same data type of input Tensor. Default: None.name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
- Returns
-
Result of
bitwise_right_shift. It is a N-D Tensor with the same data type of input Tensor. - Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.to_tensor([[10,20,40,80],[16,17,32,65]]) >>> y = paddle.to_tensor([[1,2,3,4,], [2,3,2,1]]) >>> paddle.bitwise_right_shift(x, y, is_arithmetic=True) Tensor(shape=[2, 4], dtype=int64, place=Place(gpu:0), stop_gradient=True, [[5 , 5 , 5 , 5 ], [4 , 2 , 8 , 32]])
>>> import paddle >>> x = paddle.to_tensor([[-10,-20,-40,-80],[-16,-17,-32,-65]], dtype=paddle.int8) >>> y = paddle.to_tensor([[1,2,3,4,], [2,3,2,1]], dtype=paddle.int8) >>> paddle.bitwise_right_shift(x, y, is_arithmetic=False) # logic shift Tensor(shape=[2, 4], dtype=int8, place=Place(gpu:0), stop_gradient=True, [[123, 59 , 27 , 11 ], [60 , 29 , 56 , 95 ]])
-
bitwise_right_shift_
(
y: Tensor,
is_arithmetic: bool = True,
out: Tensor | None = None,
name: str | None = None
)
Tensor
bitwise_right_shift_¶
-
Inplace version of
bitwise_right_shiftAPI, the output Tensor will be inplaced with inputx. Please refer to bitwise_left_shift.
-
bitwise_xor
(
y: Tensor,
out: Tensor | None = None,
name: str | None = None
)
Tensor
bitwise_xor¶
-
Apply
bitwise_xoron TensorXandY.\[Out = X ^\wedge Y\]Note
paddle.bitwise_xorsupports broadcasting. If you want know more about broadcasting, please refer to please refer to Introduction to Tensor .- Parameters
-
x (Tensor) – Input Tensor of
bitwise_xor. It is a N-D Tensor of bool, uint8, int8, int16, int32, int64.y (Tensor) – Input Tensor of
bitwise_xor. It is a N-D Tensor of bool, uint8, int8, int16, int32, int64.out (Tensor|None, optional) – Result of
bitwise_xor. It is a N-D Tensor with the same data type of input Tensor. Default: None.name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
- Returns
-
Result of
bitwise_xor. It is a N-D Tensor with the same data type of input Tensor. - Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.to_tensor([-5, -1, 1]) >>> y = paddle.to_tensor([4, 2, -3]) >>> res = paddle.bitwise_xor(x, y) >>> print(res) Tensor(shape=[3], dtype=int64, place=Place(cpu), stop_gradient=True, [-1, -3, -4])
-
bitwise_xor_
(
y: Tensor,
name: str | None = None
)
Tensor
bitwise_xor_¶
-
Inplace version of
bitwise_xorAPI, the output Tensor will be inplaced with inputx. Please refer to bitwise_xor.
-
block_diag
(
name: str | None = None
)
Tensor
block_diag¶
-
Create a block diagonal matrix from provided tensors.
- Parameters
-
inputs (list|tuple) –
inputsis a Tensor list or Tensor tuple, one or more tensors with 0, 1, or 2 dimensions. The data type:bool,float16,float32,float64,uint8,int8,int16,int32,int64,bfloat16,complex64,complex128.name (str|None, optional) – Name for the operation (optional, default is None).
- Returns
-
Tensor, A
Tensor. The data type is same asinputs.
Examples
>>> import paddle >>> A = paddle.to_tensor([[4], [3], [2]]) >>> B = paddle.to_tensor([7, 6, 5]) >>> C = paddle.to_tensor(1) >>> D = paddle.to_tensor([[5, 4, 3], [2, 1, 0]]) >>> E = paddle.to_tensor([[8, 7], [7, 8]]) >>> out = paddle.block_diag([A, B, C, D, E]) >>> print(out) Tensor(shape=[9, 10], dtype=int64, place=Place(gpu:0), stop_gradient=True, [[4, 0, 0, 0, 0, 0, 0, 0, 0, 0], [3, 0, 0, 0, 0, 0, 0, 0, 0, 0], [2, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 7, 6, 5, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 1, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 5, 4, 3, 0, 0], [0, 0, 0, 0, 0, 2, 1, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 8, 7], [0, 0, 0, 0, 0, 0, 0, 0, 7, 8]])
-
bmm
(
)
bmm¶
-
C++ interface function for bmm.
-
broadcast_shape
(
y_shape: Sequence[int]
)
list[int]
broadcast_shape¶
-
The function returns the shape of doing operation with broadcasting on tensors of x_shape and y_shape.
Note
If you want know more about broadcasting, please refer to Introduction to Tensor .
- Parameters
-
x_shape (list[int]|tuple[int]) – A shape of tensor.
y_shape (list[int]|tuple[int]) – A shape of tensor.
- Returns
-
list[int], the result shape.
Examples
>>> import paddle >>> shape = paddle.broadcast_shape([2, 1, 3], [1, 3, 1]) >>> shape [2, 3, 3] >>> # shape = paddle.broadcast_shape([2, 1, 3], [3, 3, 1]) >>> # ValueError (terminated with error message).
-
broadcast_shapes
(
)
list[int]
broadcast_shapes¶
-
The function returns the shape of doing operation with broadcasting on tensors of shape list.
Note
If you want know more about broadcasting, please refer to Introduction to Tensor .
- Parameters
-
*shapes (list[int]|tuple[int]) – A shape list of multiple tensors.
- Returns
-
list[int], the result shape.
Examples
>>> import paddle >>> shape = paddle.broadcast_shapes([2, 1, 3], [1, 3, 1]) >>> shape [2, 3, 3] >>> # shape = paddle.broadcast_shapes([2, 1, 3], [3, 3, 1]) >>> # ValueError (terminated with error message). >>> shape = paddle.broadcast_shapes([5, 1, 3], [1, 4, 1], [1, 1, 3]) >>> shape [5, 4, 3] >>> # shape = paddle.broadcast_shapes([5, 1, 3], [1, 4, 1], [1, 2, 3]) >>> # ValueError (terminated with error message).
-
broadcast_tensors
(
name: str | None = None
)
list[Tensor]
broadcast_tensors¶
-
Broadcast a list of tensors following broadcast semantics
Note
If you want know more about broadcasting, please refer to Introduction to Tensor .
The following figure illustrates the process of broadcasting three tensors to the same dimensions. The dimensions of the three tensors are [4, 1, 3], [2, 3], and [4, 2, 1], respectively. During broadcasting, alignment starts from the last dimension, and for each dimension, either the sizes of the two tensors in that dimension are equal, or one of the tensors has a dimension of 1, or one of the tensors lacks that dimension. In the figure below, in the last dimension, Tensor3 has a size of 1, while Tensor1 and Tensor2 have sizes of 3; thus, this dimension is expanded to 3 for all tensors. In the second-to-last dimension, Tensor1 has a size of 2, and Tensor2 and Tensor3 both have sizes of 2; hence, this dimension is expanded to 2 for all tensors. In the third-to-last dimension, Tensor2 lacks this dimension, while Tensor1 and Tensor3 have sizes of 4; consequently, this dimension is expanded to 4 for all tensors. Ultimately, all tensors are expanded to [4, 2, 3].

- Parameters
-
input (list|tuple) –
inputis a Tensor list or Tensor tuple which is with data type bool, float16, float32, float64, int32, int64, complex64, complex128. All the Tensors ininputmust have same data type. Currently we only support tensors with rank no greater than 5.name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
list(Tensor), The list of broadcasted tensors following the same order as
input.
Examples
>>> import paddle >>> x1 = paddle.rand([1, 2, 3, 4]).astype('float32') >>> x2 = paddle.rand([1, 2, 1, 4]).astype('float32') >>> x3 = paddle.rand([1, 1, 3, 1]).astype('float32') >>> out1, out2, out3 = paddle.broadcast_tensors(input=[x1, x2, x3]) >>> # out1, out2, out3: tensors broadcasted from x1, x2, x3 with shape [1,2,3,4]
-
broadcast_to
(
shape: ShapeLike,
name: str | None = None
)
Tensor
broadcast_to¶
-
Broadcast the input tensor to a given shape.
Both the number of dimensions of
xand the number of elements inshapeshould be less than or equal to 6. The dimension to broadcast to must have a value 0.The following figure shows the process of broadcasting a one-dimensional tensor of shape [3] to a two-dimensional tensor of shape [2,3] based on the shape specified by ‘shape’.
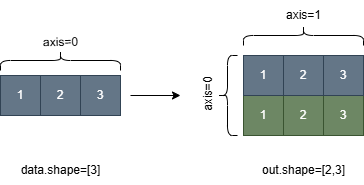
Note
Alias Support: The parameter name
inputcan be used as an alias forx, andsizecan be used as an alias forshape. For example,broadcast_to(input=tensor_x, size=[2, 3], ...)is equivalent tobroadcast_to(x=tensor_x, shape=[2, 3], ...).- Parameters
-
x (Tensor) – The input tensor, its data type is bool, float16, float32, float64, int32, int64, uint8 or uint16. alias:
input.shape (list|tuple|Tensor) – The result shape after broadcasting. The data type is int32. If shape is a list or tuple, all its elements should be integers or 0-D or 1-D Tensors with the data type int32. If shape is a Tensor, it should be an 1-D Tensor with the data type int32. The value -1 in shape means keeping the corresponding dimension unchanged. alias:
size.name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
N-D Tensor, A Tensor with the given shape. The data type is the same as
x.
Examples
>>> import paddle >>> data = paddle.to_tensor([1, 2, 3], dtype='int32') >>> out = paddle.broadcast_to(data, shape=[2, 3]) >>> print(out) Tensor(shape=[2, 3], dtype=int32, place=Place(cpu), stop_gradient=True, [[1, 2, 3], [1, 2, 3]])
-
bucketize
(
sorted_sequence: Tensor,
out_int32: bool = False,
right: bool = False,
name: str | None = None
)
Tensor
bucketize¶
-
This API is used to find the index of the corresponding 1D tensor sorted_sequence in the innermost dimension based on the given x.
- Parameters
-
x (Tensor) – An input N-D tensor value with type int32, int64, float32, float64.
sorted_sequence (Tensor) – An input 1-D tensor with type int32, int64, float32, float64. The value of the tensor monotonically increases in the innermost dimension.
out_int32 (bool, optional) – Data type of the output tensor which can be int32, int64. The default value is False, and it indicates that the output data type is int64.
right (bool, optional) – Find the upper or lower bounds of the sorted_sequence range in the innermost dimension based on the given x. If the value of the sorted_sequence is nan or inf, return the size of the innermost dimension. The default value is False and it shows the lower bounds.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
- Returns
-
Tensor (the same sizes of the x), return the tensor of int32 if set
out_int32is True, otherwise return the tensor of int64.
Examples
>>> import paddle >>> sorted_sequence = paddle.to_tensor([2, 4, 8, 16], dtype='int32') >>> x = paddle.to_tensor([[0, 8, 4, 16], [-1, 2, 8, 4]], dtype='int32') >>> out1 = paddle.bucketize(x, sorted_sequence) >>> print(out1) Tensor(shape=[2, 4], dtype=int64, place=Place(cpu), stop_gradient=True, [[0, 2, 1, 3], [0, 0, 2, 1]]) >>> out2 = paddle.bucketize(x, sorted_sequence, right=True) >>> print(out2) Tensor(shape=[2, 4], dtype=int64, place=Place(cpu), stop_gradient=True, [[0, 3, 2, 4], [0, 1, 3, 2]]) >>> out3 = x.bucketize(sorted_sequence) >>> print(out3) Tensor(shape=[2, 4], dtype=int64, place=Place(cpu), stop_gradient=True, [[0, 2, 1, 3], [0, 0, 2, 1]]) >>> out4 = x.bucketize(sorted_sequence, right=True) >>> print(out4) Tensor(shape=[2, 4], dtype=int64, place=Place(cpu), stop_gradient=True, [[0, 3, 2, 4], [0, 1, 3, 2]])
-
cast
(
dtype: DTypeLike
)
Tensor
cast¶
-
Take in the Tensor
xwithx.dtypeand cast it to the output withdtype. It’s meaningless if the output dtype equals the input dtype, but it’s fine if you do so.The following picture shows an example where a tensor of type float64 is cast to a tensor of type uint8.
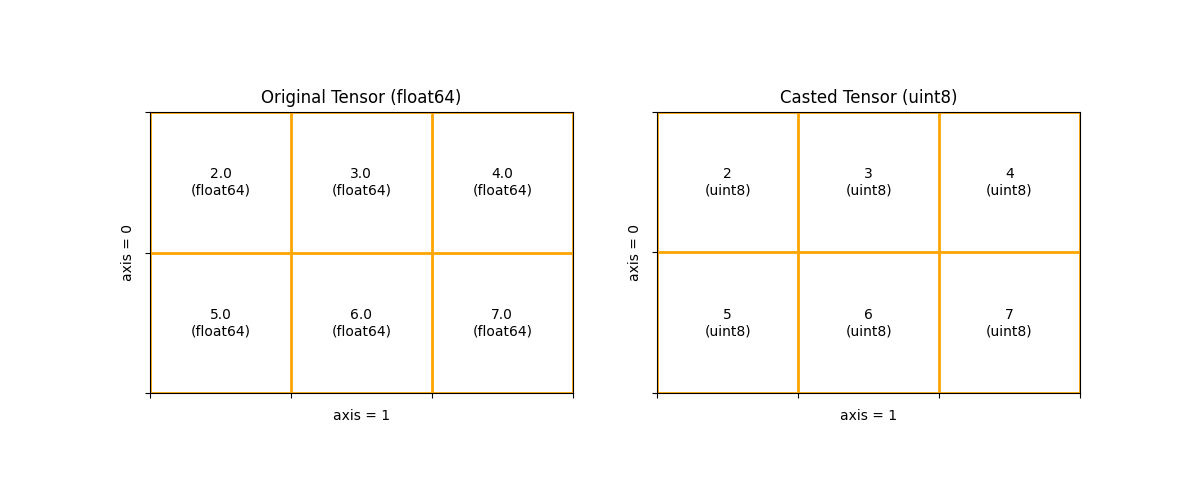
- Parameters
-
x (Tensor) – An input N-D Tensor with data type bool, float16, float32, float64, int32, int64, uint8.
dtype (paddle.dtype|np.dtype|str) – Data type of the output: bool, float16, float32, float64, int8, int32, int64, uint8.
- Returns
-
Tensor, A Tensor with the same shape as input’s.
Examples
>>> import paddle >>> x = paddle.to_tensor([2, 3, 4], 'float64') >>> y = paddle.cast(x, 'uint8')
-
cast_
(
dtype: DTypeLike
)
Tensor
cast_¶
-
Inplace version of
castAPI, the output Tensor will be inplaced with inputx. Please refer to cast.
-
cauchy_
(
loc: Numeric = 0,
scale: Numeric = 1,
name: str | None = None
)
paddle.Tensor
cauchy_¶
-
Fills the tensor with numbers drawn from the Cauchy distribution.
- Parameters
-
x (Tensor) – the tensor will be filled, The data type is float32 or float64.
loc (scalar, optional) – Location of the peak of the distribution. The data type is float32 or float64.
scale (scalar, optional) – The half-width at half-maximum (HWHM). The data type is float32 or float64. Must be positive values.
name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Returns
-
input tensor with numbers drawn from the Cauchy distribution.
- Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.randn([3, 4]) >>> x.cauchy_(1, 2) >>> >>> print(x) Tensor(shape=[3, 4], dtype=float32, place=Place(cpu), stop_gradient=True, [[ 3.80087137, 2.25415039, 2.77960515, 7.64125967], [ 0.76541221, 2.74023032, 1.99383152, -0.12685823], [ 1.45228469, 1.76275957, -4.30458832, 34.74880219]])
-
cdist
(
y: Tensor,
p: float = 2.0,
compute_mode: Literal['use_mm_for_euclid_dist_if_necessary', 'use_mm_for_euclid_dist', 'donot_use_mm_for_euclid_dist'] = 'use_mm_for_euclid_dist_if_necessary',
name: str | None = None
)
Tensor
cdist¶
-
Compute the p-norm distance between each pair of the two collections of inputs.
This function is equivalent to scipy.spatial.distance.cdist(input,’minkowski’, p=p) if \(p \in (0, \infty)\). When \(p = 0\) it is equivalent to scipy.spatial.distance.cdist(input, ‘hamming’) * M. When \(p = \infty\), the closest scipy function is scipy.spatial.distance.cdist(xn, lambda x, y: np.abs(x - y).max()).
- Parameters
-
x (Tensor) – A tensor with shape \(B \times P \times M\).
y (Tensor) – A tensor with shape \(B \times R \times M\).
p (float, optional) – The value for the p-norm distance to calculate between each vector pair. Default: \(2.0\).
compute_mode (str, optional) –
The mode for compute distance.
use_mm_for_euclid_dist_if_necessary, for p = 2.0 and (P > 25 or R > 25), it will use matrix multiplication to calculate euclid distance if possible.use_mm_for_euclid_dist, for p = 2.0, it will use matrix multiplication to calculate euclid distance.donot_use_mm_for_euclid_dist, it will not use matrix multiplication to calculate euclid distance.
Default:
use_mm_for_euclid_dist_if_necessary.name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Returns
-
Tensor, the dtype is same as input tensor.
If x has shape \(B \times P \times M\) and y has shape \(B \times R \times M\) then the output will have shape \(B \times P \times R\).
Examples
>>> import paddle >>> x = paddle.to_tensor([[0.9041, 0.0196], [-0.3108, -2.4423], [-0.4821, 1.059]], dtype=paddle.float32) >>> y = paddle.to_tensor([[-2.1763, -0.4713], [-0.6986, 1.3702]], dtype=paddle.float32) >>> distance = paddle.cdist(x, y) >>> print(distance) Tensor(shape=[3, 2], dtype=float32, place=Place(cpu), stop_gradient=True, [[3.11927032, 2.09589314], [2.71384072, 3.83217239], [2.28300953, 0.37910119]])
-
ceil
(
name: str | None = None
)
Tensor
ceil¶
-
Ceil Operator. Computes ceil of x element-wise.
\[out = \left \lceil x \right \rceil\]- Parameters
-
x (Tensor) – Input of Ceil operator, an N-D Tensor, with data type float32, float64, float16, bfloat16, uint8, int8, int16, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
- Tensor. Output of Ceil operator, a Tensor with shape same as input
-
(integer types are autocasted into float32).
Examples
>>> import paddle >>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3]) >>> out = paddle.ceil(x) >>> print(out) Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [-0., -0., 1. , 1. ])
-
ceil_
(
name=None
)
ceil_¶
-
Inplace version of
ceilAPI, the output Tensor will be inplaced with inputx. Please refer to ceil.
-
cholesky
(
upper: bool = False,
name: str | None = None
)
Tensor
cholesky¶
-
Computes the Cholesky decomposition of one symmetric positive-definite matrix or batches of symmetric positive-definite matrices.
If upper is True, the decomposition has the form \(A = U^{T}U\) , and the returned matrix \(U\) is upper-triangular. Otherwise, the decomposition has the form \(A = LL^{T}\) , and the returned matrix \(L\) is lower-triangular.
- Parameters
-
x (Tensor) – The input tensor. Its shape should be [*, M, M], where * is zero or more batch dimensions, and matrices on the inner-most 2 dimensions all should be symmetric positive-definite. Its data type should be float32 or float64.
upper (bool, optional) – The flag indicating whether to return upper or lower triangular matrices. Default: False.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, A Tensor with same shape and data type as x. It represents triangular matrices generated by Cholesky decomposition.
Examples
>>> import paddle >>> paddle.seed(2023) >>> a = paddle.rand([3, 3], dtype="float32") >>> a_t = paddle.transpose(a, [1, 0]) >>> x = paddle.matmul(a, a_t) + 1e-03 >>> out = paddle.linalg.cholesky(x, upper=False) >>> print(out) Tensor(shape=[3, 3], dtype=float32, place=Place(cpu), stop_gradient=True, [[1.04337072, 0. , 0. ], [1.06467664, 0.17859250, 0. ], [1.30602181, 0.08326444, 0.22790681]])
-
cholesky_inverse
(
upper: bool = False,
name: str | None = None
)
Tensor
cholesky_inverse¶
-
Using the Cholesky factor U to calculate the inverse matrix of a symmetric positive definite matrix, returns the matrix inv.
If upper is False, U is lower triangular matrix:
\[inv = (UU^{T})^{-1}\]If upper is True, U is upper triangular matrix:
\[inv = (U^{T}U)^{-1}\]- Parameters
-
x (Tensor) – A tensor of lower or upper triangular Cholesky decompositions of symmetric matrix with shape [N, N]. The data type of the x should be one of
float32,float64.upper (bool, optional) – If upper is False, x is lower triangular matrix, or is upper triangular matrix. Default: False.
name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Returns
-
Tensor. Computes the inverse matrix.
Examples
>>> import paddle >>> # lower triangular matrix >>> x = paddle.to_tensor([[3.,.0,.0], [5.,3.,.0], [-1.,1.,2.]]) >>> out = paddle.linalg.cholesky_inverse(x) >>> print(out) Tensor(shape=[3, 3], dtype=float32, place=Place(gpu:0), stop_gradient=True, [[ 0.61728382, -0.25925916, 0.22222219], [-0.25925916, 0.13888884, -0.08333331], [ 0.22222218, -0.08333331, 0.25000000]]) >>> # upper triangular matrix >>> out = paddle.linalg.cholesky_inverse(x.T, upper=True) >>> print(out) Tensor(shape=[3, 3], dtype=float32, place=Place(gpu:0), stop_gradient=True, [[ 0.61728382, -0.25925916, 0.22222219], [-0.25925916, 0.13888884, -0.08333331], [ 0.22222218, -0.08333331, 0.25000000]])
-
cholesky_solve
(
y: Tensor,
upper: bool = False,
name: str | None = None
)
Tensor
cholesky_solve¶
-
Solves a linear system of equations A @ X = B, given A’s Cholesky factor matrix u and matrix B.
Input x and y is 2D matrices or batches of 2D matrices. If the inputs are batches, the outputs is also batches.
- Parameters
-
x (Tensor) – Multiple right-hand sides of system of equations. Its shape should be [*, M, K], where * is zero or more batch dimensions. Its data type should be float32 or float64.
y (Tensor) – The input matrix which is upper or lower triangular Cholesky factor of square matrix A. Its shape should be [*, M, M], where * is zero or more batch dimensions. Its data type should be float32 or float64.
upper (bool, optional) – whether to consider the Cholesky factor as a lower or upper triangular matrix. Default: False.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
The solution of the system of equations. Its data type is the same as that of x.
- Return type
-
Tensor
Examples
>>> import paddle >>> u = paddle.to_tensor([[1, 1, 1], ... [0, 2, 1], ... [0, 0,-1]], dtype="float64") >>> b = paddle.to_tensor([[0], [-9], [5]], dtype="float64") >>> out = paddle.linalg.cholesky_solve(b, u, upper=True) >>> print(out) Tensor(shape=[3, 1], dtype=float64, place=Place(cpu), stop_gradient=True, [[-2.50000000], [-7. ], [ 9.50000000]])
-
chunk
(
chunks: int,
axis: int | Tensor = 0,
name: str | None = None
)
list[Tensor]
chunk¶
-
Split the input tensor into multiple sub-Tensors.
Here are some examples to explain it.
-
Given a 3-D tensor x with a shape [3, 3, 3], if we split the first dimension into three equal parts, it will output a list containing three 3-D tensors with a shape of [1, 3, 3].
-
Given a 3-D tensor x with a shape [3, 3, 3], if we split the second dimension into three equal parts, it will output a list containing three 3-D tensors with a shape of [3, 1, 3].
-
Given a 3-D tensor x with a shape [3, 3, 3], if we split the third dimension into three equal parts, it will output a list containing three 3-D tensors with a shape of [3, 3, 1].
The following figure illustrates the first example.
Note
Alias Support: The parameter name
inputcan be used as an alias forx, and the parameter namedimcan be used as an alias foraxis. For example,chunk(input=tensor_x, dim=1)is equivalent tochunk(x=tensor_x, axis=1).- Parameters
-
x (Tensor) – A N-D Tensor. The data type is bool, float16, float32, float64, int32 or int64. alias:
input.chunks (int) – The number of tensor to be split along the certain axis.
axis (int|Tensor, optional) – The axis along which to split, it can be a integer or a
0-D Tensorwith shape [] and data typeint32orint64. If :math::axis < 0, the axis to split along is \(rank(x) + axis\). Default is 0. alias:dim.name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name .
- Returns
-
list(Tensor), The list of segmented Tensors.
Examples
>>> import paddle >>> x = paddle.rand([3, 9, 5]) >>> out0, out1, out2 = paddle.chunk(x, chunks=3, axis=1) >>> # out0.shape [3, 3, 5] >>> # out1.shape [3, 3, 5] >>> # out2.shape [3, 3, 5] >>> # axis is negative, the real axis is (rank(x) + axis) which real >>> # value is 1. >>> out0, out1, out2 = paddle.chunk(x, chunks=3, axis=-2) >>> # out0.shape [3, 3, 5] >>> # out1.shape [3, 3, 5] >>> # out2.shape [3, 3, 5]
-
-
clip
(
min: float | None = None,
max: float | None = None,
name: str | None = None,
*,
out: Tensor | None = None
)
Tensor
clip¶
-
This operator clip all elements in input into the range [ min, max ] and return a resulting tensor as the following equation:
\[Out = MIN(MAX(x, min), max)\]Note
Alias Support: The parameter name
inputcan be used as an alias forx. For example,clip(input=tensor_x)is equivalent toclip(x=tensor_x).- Parameters
-
x (Tensor) – An N-D Tensor with data type bfloat16, float16, float32, float64, int32 or int64. alias:
input.min (float|int|Tensor, optional) – The lower bound with type
float,intor a0-D Tensorwith shape [] and typebfloat16,float16,float32,float64,int32.max (float|int|Tensor, optional) – The upper bound with type
float,intor a0-D Tensorwith shape [] and typebfloat16,float16,float32,float64,int32.name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
out (Tensor, optional) – The output Tensor. If set, the result will be stored in this Tensor. Default: None.
- Returns
-
A Tensor with the same data shape as input. If either min or max is a floating-point value/Tensor, the output tensor will have a data type of
float32. Otherwise, the output tensor will inherit the same data type as the input. - Return type
-
Tensor
Examples
>>> import paddle >>> x1 = paddle.to_tensor([[1.2, 3.5], [4.5, 6.4]], 'float32') >>> out1 = paddle.clip(x1, min=3.5, max=5.0) >>> out1 Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True, [[3.50000000, 3.50000000], [4.50000000, 5. ]]) >>> out2 = paddle.clip(x1, min=2.5) >>> out2 Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True, [[2.50000000, 3.50000000], [4.50000000, 6.40000010]])
-
clip_
(
min: float | None = None,
max: float | None = None,
name: str | None = None
)
Tensor
clip_¶
-
Inplace version of
clipAPI, the output Tensor will be inplaced with inputx. Please refer to api_paddle_clip.
-
combinations
(
r: int = 2,
with_replacement: bool = False,
name: str | None = None
)
Tensor
combinations¶
-
Compute combinations of length r of the given tensor. The behavior is similar to python’s itertools.combinations when with_replacement is set to False, and itertools.combinations_with_replacement when with_replacement is set to True.
- Parameters
-
x (Tensor) – 1-D input Tensor, the data type is float16, float32, float64, int32 or int64.
r (int, optional) – number of elements to combine, default value is 2.
with_replacement (bool, optional) – whether to allow duplication in combination, default value is False.
name (str|None, optional) – Name for the operation (optional, default is None).For more information, please refer to api_guide_Name.
- Returns
-
out (Tensor). Tensor concatenated by combinations, same dtype with x.
Examples
>>> import paddle >>> x = paddle.to_tensor([1, 2, 3], dtype='int32') >>> res = paddle.combinations(x) >>> print(res) Tensor(shape=[3, 2], dtype=int32, place=Place(gpu:0), stop_gradient=True, [[1, 2], [1, 3], [2, 3]])
-
concat
(
axis: int | Tensor = 0,
name: str | None = None,
*,
out: Tensor | None = None
)
Tensor
concat¶
-
Concatenates the input along the axis. It doesn’t support 0-D Tensor because it requires a certain axis, and 0-D Tensor doesn’t have any axis.
The image illustrates a typical case of the concat operation. Two three-dimensional tensors with shapes [2, 3, 4] are concatenated along different axes, resulting in tensors of different shapes. The effects of concatenation along various dimensions are clearly visible.
Note
Alias Support: The parameter name
tensorscan be used as an alias forx, anddimcan be used as an alias foraxis. For example,concat(tensors=tensor_x, dim=1, ...)is equivalent toconcat(x=tensor_x, axis=1, ...).- Parameters
-
x (list|tuple) –
xis a Tensor list or Tensor tuple which is with data type bool, float16, bfloat16, float32, float64, int8, int16, int32, int64, uint8, uint16, complex64, complex128. All the Tensors inxmust have same data type. alias:tensors.axis (int|Tensor, optional) – Specify the axis to operate on the input Tensors. Tt should be integer or 0-D int Tensor with shape []. The effective range is [-R, R), where R is Rank(x). When
axis < 0, it works the same way asaxis+R. Default is 0. alias:dim.name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
out (Tensor|None, optional) – The output Tensor. If set, the result will be stored in this Tensor. Default is None.
- Returns
-
Tensor, A Tensor with the same data type as
x.
Examples
>>> import paddle >>> x1 = paddle.to_tensor([[1, 2, 3], ... [4, 5, 6]]) >>> x2 = paddle.to_tensor([[11, 12, 13], ... [14, 15, 16]]) >>> x3 = paddle.to_tensor([[21, 22], ... [23, 24]]) >>> zero = paddle.full(shape=[1], dtype='int32', fill_value=0) >>> # When the axis is negative, the real axis is (axis + Rank(x)) >>> # As follow, axis is -1, Rank(x) is 2, the real axis is 1 >>> out1 = paddle.concat(x=[x1, x2, x3], axis=-1) >>> out2 = paddle.concat(x=[x1, x2], axis=0) >>> out3 = paddle.concat(x=[x1, x2], axis=zero) >>> print(out1) Tensor(shape=[2, 8], dtype=int64, place=Place(cpu), stop_gradient=True, [[1 , 2 , 3 , 11, 12, 13, 21, 22], [4 , 5 , 6 , 14, 15, 16, 23, 24]]) >>> print(out2) Tensor(shape=[4, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[1 , 2 , 3 ], [4 , 5 , 6 ], [11, 12, 13], [14, 15, 16]]) >>> print(out3) Tensor(shape=[4, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[1 , 2 , 3 ], [4 , 5 , 6 ], [11, 12, 13], [14, 15, 16]])
-
cond
(
p: float | _POrder | None = None,
name: str | None = None
)
Tensor
cond¶
-
Computes the condition number of a matrix or batches of matrices with respect to a matrix norm
p.- Parameters
-
x (Tensor) – The input tensor could be tensor of shape
(*, m, n)where*is zero or more batch dimensions forpin(2, -2), or of shape(*, n, n)where every matrix is invertible for any supportedp. And the input data type could befloat32orfloat64.p (float|string, optional) – Order of the norm. Supported values are fro, nuc, 1, -1, 2, -2, inf, -inf. Default value is None, meaning that the order of the norm is 2.
name (str, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
- Returns
-
computing results of condition number, its data type is the same as input Tensor
x. - Return type
-
Tensor
Examples
>>> import paddle >>> paddle.seed(2023) >>> x = paddle.to_tensor([[1., 0, -1], [0, 1, 0], [1, 0, 1]]) >>> # compute conditional number when p is None >>> out = paddle.linalg.cond(x) >>> print(out) Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 1.41421378) >>> # compute conditional number when order of the norm is 'fro' >>> out_fro = paddle.linalg.cond(x, p='fro') >>> print(out_fro) Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 3.16227770) >>> # compute conditional number when order of the norm is 'nuc' >>> out_nuc = paddle.linalg.cond(x, p='nuc') >>> print(out_nuc) Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 9.24264145) >>> # compute conditional number when order of the norm is 1 >>> out_1 = paddle.linalg.cond(x, p=1) >>> print(out_1) Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 2.) >>> # compute conditional number when order of the norm is -1 >>> out_minus_1 = paddle.linalg.cond(x, p=-1) >>> print(out_minus_1) Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 1.) >>> # compute conditional number when order of the norm is 2 >>> out_2 = paddle.linalg.cond(x, p=2) >>> print(out_2) Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 1.41421378) >>> # compute conditional number when order of the norm is -1 >>> out_minus_2 = paddle.linalg.cond(x, p=-2) >>> print(out_minus_2) Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 0.70710671) >>> # compute conditional number when order of the norm is inf >>> out_inf = paddle.linalg.cond(x, p=float("inf")) >>> print(out_inf) Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 2.) >>> # compute conditional number when order of the norm is -inf >>> out_minus_inf = paddle.linalg.cond(x, p=-float("inf")) >>> print(out_minus_inf) Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 1.) >>> a = paddle.randn([2, 4, 4]) >>> print(a) Tensor(shape=[2, 4, 4], dtype=float32, place=Place(cpu), stop_gradient=True, [[[ 0.06132207, 1.11349595, 0.41906244, -0.24858207], [-1.85169315, -1.50370061, 1.73954511, 0.13331604], [ 1.66359663, -0.55764782, -0.59911072, -0.57773495], [-1.03176904, -0.33741450, -0.29695082, -1.50258386]], [[ 0.67233968, -1.07747352, 0.80170447, -0.06695852], [-1.85003340, -0.23008066, 0.65083790, 0.75387722], [ 0.61212337, -0.52664012, 0.19209868, -0.18707706], [-0.00711021, 0.35236868, -0.40404350, 1.28656745]]]) >>> a_cond_fro = paddle.linalg.cond(a, p='fro') >>> print(a_cond_fro) Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True, [6.37173700 , 35.15114594]) >>> b = paddle.randn([2, 3, 4]) >>> print(b) Tensor(shape=[2, 3, 4], dtype=float32, place=Place(cpu), stop_gradient=True, [[[ 0.03306439, 0.70149767, 0.77064633, -0.55978841], [-0.84461296, 0.99335045, -1.23486686, 0.59551388], [-0.63035583, -0.98797107, 0.09410731, 0.47007179]], [[ 0.85850012, -0.98949534, -1.63086998, 1.07340240], [-0.05492965, 1.04750168, -2.33754158, 1.16518629], [ 0.66847134, -1.05326962, -0.05703246, -0.48190674]]]) >>> b_cond_2 = paddle.linalg.cond(b, p=2) >>> print(b_cond_2) Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True, [2.86566353, 6.85834455])
-
conj
(
name: str | None = None
)
Tensor
conj¶
-
This function computes the conjugate of the Tensor elementwisely.
- Parameters
-
x (Tensor) – The input Tensor which hold the complex numbers. Optional data types are: bfloat16, float16, complex64, complex128, float32, float64, int32 or int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
The conjugate of input. The shape and data type is the same with input. If the elements of tensor is real type such as float32, float64, int32 or int64, the out is the same with input.
- Return type
-
out (Tensor)
Examples
>>> import paddle >>> data = paddle.to_tensor([[1+1j, 2+2j, 3+3j], [4+4j, 5+5j, 6+6j]]) >>> data Tensor(shape=[2, 3], dtype=complex64, place=Place(cpu), stop_gradient=True, [[(1+1j), (2+2j), (3+3j)], [(4+4j), (5+5j), (6+6j)]]) >>> conj_data = paddle.conj(data) >>> conj_data Tensor(shape=[2, 3], dtype=complex64, place=Place(cpu), stop_gradient=True, [[(1-1j), (2-2j), (3-3j)], [(4-4j), (5-5j), (6-6j)]])
-
contiguous
(
)
contiguous¶
-
Variable don’t have ‘contiguous’ interface in static graph mode But this interface can greatly facilitate dy2static. So we give a warning here and return None.
-
copysign
(
y: Tensor | float,
name: str | None = None
)
Tensor
copysign¶
-
Create a new floating-point tensor with the magnitude of input
xand the sign ofy, elementwise.- Equation:
-
\[\begin{split}copysign(x_{i},y_{i})=\left\{\begin{matrix} & -|x_{i}| & if \space y_{i} <= -0.0\\ & |x_{i}| & if \space y_{i} >= 0.0 \end{matrix}\right.\end{split}\]
- Parameters
-
x (Tensor) – The input Tensor, magnitudes, the data type is bool, uint8, int8, int16, int32, int64, bfloat16, float16, float32, float64.
y (Tensor|float) – contains value(s) whose signbit(s) are applied to the magnitudes in input.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
out (Tensor), the output tensor. The data type is the same as the input tensor.
Examples
>>> import paddle >>> x = paddle.to_tensor([1, 2, 3], dtype='float64') >>> y = paddle.to_tensor([-1, 1, -1], dtype='float64') >>> out = paddle.copysign(x, y) >>> print(out) Tensor(shape=[3], dtype=float64, place=Place(gpu:0), stop_gradient=True, [-1., 2., -3.])
>>> import paddle >>> x = paddle.to_tensor([1, 2, 3], dtype='float64') >>> y = paddle.to_tensor([-2], dtype='float64') >>> res = paddle.copysign(x, y) >>> print(res) Tensor(shape=[3], dtype=float64, place=Place(gpu:0), stop_gradient=True, [-1., -2., -3.])
>>> import paddle >>> x = paddle.to_tensor([1, 2, 3], dtype='float64') >>> y = paddle.to_tensor([0.0], dtype='float64') >>> out = paddle.copysign(x, y) >>> print(out) Tensor(shape=[3], dtype=float64, place=Place(gpu:0), stop_gradient=True, [1., 2., 3.])
>>> import paddle >>> x = paddle.to_tensor([1, 2, 3], dtype='float64') >>> y = paddle.to_tensor([-0.0], dtype='float64') >>> out = paddle.copysign(x, y) >>> print(out) Tensor(shape=[3], dtype=float64, place=Place(gpu:0), stop_gradient=True, [-1., -2., -3.])
-
copysign_
(
y: Tensor,
name: str | None = None
)
Tensor
copysign_¶
-
Inplace version of
copysignAPI, the output Tensor will be inplaced with inputx. Please refer to copysign.
-
corrcoef
(
rowvar: bool = True,
name: str | None = None
)
Tensor
corrcoef¶
-
A correlation coefficient matrix indicate the correlation of each pair variables in the input matrix. For example, for an N-dimensional samples X=[x1,x2,…xN]T, then the correlation coefficient matrix element Rij is the correlation of xi and xj. The element Rii is the covariance of xi itself.
The relationship between the correlation coefficient matrix R and the covariance matrix C, is
\[R_{ij} = \frac{ C_{ij} } { \sqrt{ C_{ii} * C_{jj} } }\]The values of R are between -1 and 1.
- Parameters
-
x (Tensor) – A N-D(N<=2) Tensor containing multiple variables and observations. By default, each row of x represents a variable. Also see rowvar below.
rowvar (bool, optional) – If rowvar is True (default), then each row represents a variable, with observations in the columns. Default: True.
name (str|None, optional) – Name of the output. It’s used to print debug info for developers. Details: api_guide_Name. Default: None.
- Returns
-
The correlation coefficient matrix of the variables.
Examples
>>> import paddle >>> paddle.seed(2023) >>> xt = paddle.rand((3,4)) >>> print(paddle.linalg.corrcoef(xt)) Tensor(shape=[3, 3], dtype=float32, place=Place(cpu), stop_gradient=True, [[ 0.99999988, -0.47689581, -0.89559376], [-0.47689593, 1. , 0.16345492], [-0.89559382, 0.16345496, 1. ]])
-
cos
(
)
cos¶
-
C++ interface function for cos.
-
cos_
(
name=None
)
cos_¶
-
Inplace version of
cosAPI, the output Tensor will be inplaced with inputx. Please refer to cos.
-
cosh
(
name: str | None = None
)
Tensor
cosh¶
-
Cosh Activation Operator.
Input range (-inf, inf), output range (1, inf).
\[out = \frac{exp(x)+exp(-x)}{2}\]- Parameters
-
x (Tensor) – Input of Cosh operator, an N-D Tensor, with data type float32, float64, float16, bfloat16, uint8, int8, int16, int32, int64, complex64 or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
- Tensor. Output of Cosh operator, a Tensor with shape same as input
-
(integer types are autocasted into float32).
Examples
>>> import paddle >>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3]) >>> out = paddle.cosh(x) >>> print(out) Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [1.08107233, 1.02006674, 1.00500417, 1.04533851])
-
cosh_
(
name=None
)
cosh_¶
-
Inplace version of
coshAPI, the output Tensor will be inplaced with inputx. Please refer to cosh.
-
count_nonzero
(
axis: int | Sequence[int] | None = None,
keepdim: bool = False,
name: str | None = None
)
Tensor
count_nonzero¶
-
Counts the number of non-zero values in the tensor x along the specified axis.
- Parameters
-
x (Tensor) – An N-D Tensor, the data type is bool, float16, float32, float64, int32 or int64.
axis (int|list|tuple, optional) – The dimensions along which the sum is performed. If
None, sum all elements ofxand return a Tensor with a single element, otherwise must be in the range \([-rank(x), rank(x))\). If \(axis[i] < 0\), the dimension to reduce is \(rank + axis[i]\).keepdim (bool, optional) – Whether to reserve the reduced dimension in the output Tensor. The result Tensor will have one fewer dimension than the
xunlesskeepdimis true, default value is False.name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Results of count operation on the specified axis of input Tensor x, it’s data type is ‘int64’.
- Return type
-
Tensor
Examples
>>> import paddle >>> # x is a 2-D Tensor: >>> x = paddle.to_tensor([[0., 1.1, 1.2], [0., 0., 1.3], [0., 0., 0.]]) >>> out1 = paddle.count_nonzero(x) >>> out1 Tensor(shape=[], dtype=int64, place=Place(cpu), stop_gradient=True, 3) >>> out2 = paddle.count_nonzero(x, axis=0) >>> out2 Tensor(shape=[3], dtype=int64, place=Place(cpu), stop_gradient=True, [0, 1, 2]) >>> out3 = paddle.count_nonzero(x, axis=0, keepdim=True) >>> out3 Tensor(shape=[1, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[0, 1, 2]]) >>> out4 = paddle.count_nonzero(x, axis=1) >>> out4 Tensor(shape=[3], dtype=int64, place=Place(cpu), stop_gradient=True, [2, 1, 0]) >>> out5 = paddle.count_nonzero(x, axis=1, keepdim=True) >>> out5 Tensor(shape=[3, 1], dtype=int64, place=Place(cpu), stop_gradient=True, [[2], [1], [0]]) >>> # y is a 3-D Tensor: >>> y = paddle.to_tensor([[[0., 1.1, 1.2], [0., 0., 1.3], [0., 0., 0.]], ... [[0., 2.5, 2.6], [0., 0., 2.4], [2.1, 2.2, 2.3]]]) >>> out6 = paddle.count_nonzero(y, axis=[1, 2]) >>> out6 Tensor(shape=[2], dtype=int64, place=Place(cpu), stop_gradient=True, [3, 6]) >>> out7 = paddle.count_nonzero(y, axis=[0, 1]) >>> out7 Tensor(shape=[3], dtype=int64, place=Place(cpu), stop_gradient=True, [1, 3, 5])
-
cov
(
rowvar: bool = True,
ddof: bool = True,
fweights: Tensor | None = None,
aweights: Tensor | None = None,
name: str | None = None
)
Tensor
cov¶
-
Estimate the covariance matrix of the input variables, given data and weights.
A covariance matrix is a square matrix, indicate the covariance of each pair variables in the input matrix. For example, for an N-dimensional samples X=[x1,x2,…xN]T, then the covariance matrix element Cij is the covariance of xi and xj. The element Cii is the variance of xi itself.
- Parameters
-
x (Tensor) – A N-D(N<=2) Tensor containing multiple variables and observations. By default, each row of x represents a variable. Also see rowvar below.
rowvar (bool, optional) – If rowvar is True (default), then each row represents a variable, with observations in the columns. Default: True.
ddof (bool, optional) – If ddof=True will return the unbiased estimate, and ddof=False will return the simple average. Default: True.
fweights (Tensor, optional) – 1-D Tensor of integer frequency weights; The number of times each observation vector should be repeated. Default: None.
aweights (Tensor, optional) – 1-D Tensor of observation vector weights. How important of the observation vector, larger data means this element is more important. Default: None.
name (str|None, optional) – Name of the output. Default is None. It’s used to print debug info for developers. Details: api_guide_Name .
- Returns
-
The covariance matrix Tensor of the variables.
- Return type
-
Tensor
Examples
>>> import paddle >>> paddle.seed(2023) >>> xt = paddle.rand((3, 4)) >>> paddle.linalg.cov(xt) >>> print(xt) Tensor(shape=[3, 4], dtype=float32, place=Place(cpu), stop_gradient=True, [[0.86583614, 0.52014720, 0.25960937, 0.90525323], [0.42400089, 0.40641287, 0.97020894, 0.74437362], [0.51785129, 0.73292869, 0.97786582, 0.04315904]])
-
cpu
(
)
cpu¶
-
In dy2static, Variable also needs cpu() and cuda() interface. But, the underneath operator has only forward op but not backward one.
- Returns
-
The tensor which has copied to cpu place.
Examples
In Static Graph Mode:
>>> import paddle >>> paddle.enable_static() >>> x = paddle.static.data(name="x", shape=[2,2], dtype='float32') >>> y = x.cpu()
-
create_parameter
(
dtype: DTypeLike,
name: str | None = None,
attr: ParamAttrLike | None = None,
is_bias: bool = False,
default_initializer: paddle.nn.initializer.Initializer | None = None
)
paddle.Tensor
[source]
create_parameter¶
-
This function creates a parameter. The parameter is a learnable variable, which can have gradient, and can be optimized.
Note
This is a very low-level API. This API is useful when you create operator by your self, instead of using layers.
- Parameters
-
shape (list of int) – Shape of the parameter
dtype (str) – Data type of the parameter. It can be set as ‘float16’, ‘float32’, ‘float64’.
name (str|None, optional) – For detailed information, please refer to api_guide_Name . Usually name is no need to set and None by default.
attr (ParamAttr|None, optional) – Attribute object of the specified argument. For detailed information, please refer to ParamAttr None by default, which means that ParamAttr will be initialized as it is.
is_bias (bool, optional) – This can affect which default initializer is chosen when default_initializer is None. If is_bias, initializer.Constant(0.0) will be used. Otherwise, Xavier() will be used.
default_initializer (Initializer|None, optional) – Initializer for the parameter
- Returns
-
The created parameter.
Examples
>>> import paddle >>> paddle.enable_static() >>> W = paddle.create_parameter(shape=[784, 200], dtype='float32')
-
create_tensor
(
name: str | None = None,
persistable: bool = False
)
paddle.Tensor
create_tensor¶
-
Create a variable, which will hold a Tensor with data type dtype.
- Parameters
-
dtype (string|numpy.dtype) – the data type of Tensor to be created, the data type is bool, float16, float32, float64, int8, int16, int32 and int64.
name (string, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name
persistable (bool) – Set the persistable flag of the create tensor. default value is False.
- Returns
-
The tensor to be created according to dtype.
- Return type
-
Variable
Examples
>>> import paddle >>> tensor = paddle.tensor.create_tensor(dtype='float32')
-
cross
(
y: Tensor,
axis: int = 9,
name: str | None = None
)
Tensor
cross¶
-
Computes the cross product between two tensors along an axis.
Inputs must have the same shape, and the length of their axes should be equal to 3. If axis is not given, it defaults to the first axis found with the length 3.
- Parameters
-
x (Tensor) – The first input tensor, the data type is float16, float32, float64, int32, int64, complex64, complex128.
y (Tensor) – The second input tensor, the data type is float16, float32, float64, int32, int64, complex64, complex128.
axis (int, optional) – The axis along which to compute the cross product. It defaults to be 9 which indicates using the first axis found with the length 3.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor. A Tensor with same data type as x.
Examples
>>> import paddle >>> x = paddle.to_tensor([[1.0, 1.0, 1.0], ... [2.0, 2.0, 2.0], ... [3.0, 3.0, 3.0]]) >>> y = paddle.to_tensor([[1.0, 1.0, 1.0], ... [1.0, 1.0, 1.0], ... [1.0, 1.0, 1.0]]) ... >>> z1 = paddle.cross(x, y) >>> print(z1) Tensor(shape=[3, 3], dtype=float32, place=Place(cpu), stop_gradient=True, [[-1., -1., -1.], [ 2., 2., 2.], [-1., -1., -1.]]) >>> z2 = paddle.cross(x, y, axis=1) >>> print(z2) Tensor(shape=[3, 3], dtype=float32, place=Place(cpu), stop_gradient=True, [[0., 0., 0.], [0., 0., 0.], [0., 0., 0.]])
-
cuda
(
device_id=None,
blocking=True
)
cuda¶
-
In dy2static, Variable also needs cpu() and cuda() interface. But, the underneath operator has only forward op but not backward one.
- Parameters
-
self (Variable) – The variable itself.
device_id (int, optional) – The destination GPU device id. Default: None, means current device. We add this argument for dy2static translation, please do not use it.
blocking (bool, optional) – Whether blocking or not, Default: True. We add this argument for dy2static translation, please do not use it.
- Returns
-
The tensor which has copied to cuda place.
Examples
In Static Graph Mode:
>>> import paddle >>> paddle.enable_static() >>> x = paddle.static.data(name="x", shape=[2,2], dtype='float32') >>> y = x.cpu() >>> z = y.cuda()
-
cummax
(
axis: int | None = None,
dtype: DTypeLike = 'int64',
name: str | None = None
)
tuple[Tensor, Tensor]
cummax¶
-
The cumulative max of the elements along a given axis.
Note
The first element of the result is the same as the first element of the input.
- Parameters
-
x (Tensor) – The input tensor needed to be cummaxed.
axis (int, optional) – The dimension to accumulate along. -1 means the last dimension. The default (None) is to compute the cummax over the flattened array.
dtype (str|paddle.dtype|np.dtype, optional) – The data type of the indices tensor, can be int32, int64. The default value is int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
out (Tensor), The result of cummax operation. The dtype of cummax result is same with input x.
indices (Tensor), The corresponding index results of cummax operation.
Examples
>>> import paddle >>> data = paddle.to_tensor([-1, 5, 0, -2, -3, 2]) >>> data = paddle.reshape(data, (2, 3)) >>> value, indices = paddle.cummax(data) >>> value Tensor(shape=[6], dtype=int64, place=Place(cpu), stop_gradient=True, [-1, 5, 5, 5, 5, 5]) >>> indices Tensor(shape=[6], dtype=int64, place=Place(cpu), stop_gradient=True, [0, 1, 1, 1, 1, 1]) >>> value, indices = paddle.cummax(data, axis=0) >>> value Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[-1, 5, 0], [-1, 5, 2]]) >>> indices Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[0, 0, 0], [0, 0, 1]]) >>> value, indices = paddle.cummax(data, axis=-1) >>> value Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[-1, 5, 5], [-2, -2, 2]]) >>> indices Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[0, 1, 1], [0, 0, 2]]) >>> value, indices = paddle.cummax(data, dtype='int64') >>> assert indices.dtype == paddle.int64
-
cummin
(
axis: int | None = None,
dtype: DTypeLike = 'int64',
name: str | None = None
)
tuple[Tensor, Tensor]
cummin¶
-
The cumulative min of the elements along a given axis.
Note
The first element of the result is the same as the first element of the input.
- Parameters
-
x (Tensor) – The input tensor needed to be cummined.
axis (int, optional) – The dimension to accumulate along. -1 means the last dimension. The default (None) is to compute the cummin over the flattened array.
dtype (str|paddle.dtype|np.dtype, optional) – The data type of the indices tensor, can be int32, int64. The default value is int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
out (Tensor), The result of cummin operation. The dtype of cummin result is same with input x.
indices (Tensor), The corresponding index results of cummin operation.
Examples
>>> import paddle >>> data = paddle.to_tensor([-1, 5, 0, -2, -3, 2]) >>> data = paddle.reshape(data, (2, 3)) >>> value, indices = paddle.cummin(data) >>> value Tensor(shape=[6], dtype=int64, place=Place(cpu), stop_gradient=True, [-1, -1, -1, -2, -3, -3]) >>> indices Tensor(shape=[6], dtype=int64, place=Place(cpu), stop_gradient=True, [0, 0, 0, 3, 4, 4]) >>> value, indices = paddle.cummin(data, axis=0) >>> value Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[-1, 5, 0], [-2, -3, 0]]) >>> indices Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[0, 0, 0], [1, 1, 0]]) >>> value, indices = paddle.cummin(data, axis=-1) >>> value Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[-1, -1, -1], [-2, -3, -3]]) >>> indices Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[0, 0, 0], [0, 1, 1]]) >>> value, indices = paddle.cummin(data, dtype='int64') >>> assert indices.dtype == paddle.int64
-
cumprod
(
dim: int | None = None,
dtype: DTypeLike | None = None,
name: str | None = None
)
Tensor
cumprod¶
-
Compute the cumulative product of the input tensor x along a given dimension dim.
Note
The first element of the result is the same as the first element of the input.
- Parameters
-
x (Tensor) – the input tensor need to be cumproded.
dim (int|None, optional) – the dimension along which the input tensor will be accumulated. It need to be in the range of [-x.rank, x.rank) or None, where x.rank means the dimensions of the input tensor x and -1 means the last dimension. The default (None) is to compute the cumprod over the flattened array.
dtype (str|core.VarDesc.VarType|core.DataType|np.dtype, optional) – The data type of the output tensor, can be bfloat16, float16, float32, float64, int32, int64, complex64, complex128. If specified, the input tensor is casted to dtype before the operation is performed. This is useful for preventing data type overflows. The default value is None.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, the result of cumprod operator.
Examples
>>> import paddle >>> data = paddle.arange(12) >>> data = paddle.reshape(data, (3, 4)) >>> data Tensor(shape=[3, 4], dtype=int64, place=Place(cpu), stop_gradient=True, [[0 , 1 , 2 , 3 ], [4 , 5 , 6 , 7 ], [8 , 9 , 10, 11]]) >>> y = paddle.cumprod(data, dim=0) >>> y Tensor(shape=[3, 4], dtype=int64, place=Place(cpu), stop_gradient=True, [[0 , 1 , 2 , 3 ], [0 , 5 , 12 , 21 ], [0 , 45 , 120, 231]]) >>> y = paddle.cumprod(data, dim=-1) >>> y Tensor(shape=[3, 4], dtype=int64, place=Place(cpu), stop_gradient=True, [[0 , 0 , 0 , 0 ], [4 , 20 , 120 , 840 ], [8 , 72 , 720 , 7920]]) >>> y = paddle.cumprod(data, dim=1, dtype='float64') >>> y Tensor(shape=[3, 4], dtype=float64, place=Place(cpu), stop_gradient=True, [[0. , 0. , 0. , 0. ], [4. , 20. , 120. , 840. ], [8. , 72. , 720. , 7920.]]) >>> assert y.dtype == paddle.float64
-
cumprod_
(
dim: int | None = None,
dtype: DTypeLike | None = None,
name: str | None = None
)
Tensor
cumprod_¶
-
Inplace version of
cumprodAPI, the output Tensor will be inplaced with inputx. Please refer to cumprod.
-
cumsum
(
axis: int | None = None,
dtype: DTypeLike | None = None,
name: str | None = None,
*,
out: Tensor | None = None
)
Tensor
cumsum¶
-
The cumulative sum of the elements along a given axis.
Note
The first element of the result is the same as the first element of the input.
Note
Alias Support: The parameter name
inputcan be used as an alias forx, anddimcan be used as an alias foraxis. For example,cumsum(input=tensor_x, dim=1, ...)is equivalent tocumsum(x=tensor_x, axis=1, ...).- Parameters
-
x (Tensor) – The input tensor needed to be cumsumed. alias:
input.axis (int, optional) – The dimension to accumulate along. -1 means the last dimension. The default (None) is to compute the cumsum over the flattened array. alias:
dim.dtype (str|paddle.dtype|np.dtype|None, optional) – The data type of the output tensor, can be bfloat16, float16, float32, float64, int32, int64, complex64, complex128. By default, it is int64 if the input x is int8/int16/int32; otherwise, it is None. If it is not None, the input tensor is casted to dtype before the operation is performed. This is useful for preventing data type overflows.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
out (Tensor, optional) – The output tensor. If provided, the result will be stored in this tensor.
- Returns
-
Tensor, the result of cumsum operator.
Examples
>>> import paddle >>> data = paddle.arange(12) >>> data = paddle.reshape(data, (3, 4)) >>> y = paddle.cumsum(data) >>> y Tensor(shape=[12], dtype=int64, place=Place(cpu), stop_gradient=True, [0 , 1 , 3 , 6 , 10, 15, 21, 28, 36, 45, 55, 66]) >>> y = paddle.cumsum(data, axis=0) >>> y Tensor(shape=[3, 4], dtype=int64, place=Place(cpu), stop_gradient=True, [[0 , 1 , 2 , 3 ], [4 , 6 , 8 , 10], [12, 15, 18, 21]]) >>> y = paddle.cumsum(data, axis=-1) >>> y Tensor(shape=[3, 4], dtype=int64, place=Place(cpu), stop_gradient=True, [[0 , 1 , 3 , 6 ], [4 , 9 , 15, 22], [8 , 17, 27, 38]]) >>> y = paddle.cumsum(data, dtype='float64') >>> assert y.dtype == paddle.float64
-
cumsum_
(
axis: int | None = None,
dtype: DTypeLike | None = None,
name: str | None = None
)
Tensor
cumsum_¶
-
Inplace version of
cumprodAPI, the output Tensor will be inplaced with inputx. Please refer to cumprod.
-
cumulative_trapezoid
(
x: Tensor | None = None,
dx: float | None = None,
axis: int = -1,
name: str | None = None
)
Tensor
cumulative_trapezoid¶
-
Integrate along the given axis using the composite trapezoidal rule. Use the cumsum method
- Parameters
-
y (Tensor) – Input tensor to integrate. It’s data type should be float16, float32, float64.
x (Tensor|None, optional) – The sample points corresponding to the
yvalues, the same type asy. It is known that the size ofyis [d_1, d_2, … , d_n] and \(axis=k\), then the size ofxcan only be [d_k] or [d_1, d_2, … , d_n ]. Ifxis None, the sample points are assumed to be evenly spaceddxapart. The default is None.dx (float|None, optional) – The spacing between sample points when
xis None. If neitherxnordxis provided then the default is \(dx = 1\).axis (int, optional) – The axis along which to integrate. The default is -1.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, Definite integral of
yis N-D tensor as approximated along a single axis by the trapezoidal rule. The result is an N-D tensor.
Examples
>>> import paddle >>> y = paddle.to_tensor([4, 5, 6], dtype='float32') >>> paddle.cumulative_trapezoid(y) Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True, [4.50000000, 10. ]) >>> paddle.cumulative_trapezoid(y, dx=2.) >>> # Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True, >>> # [9. , 20.]) >>> y = paddle.to_tensor([4, 5, 6], dtype='float32') >>> x = paddle.to_tensor([1, 2, 3], dtype='float32') >>> paddle.cumulative_trapezoid(y, x) Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True, [4.50000000, 10. ]) >>> y = paddle.to_tensor([1, 2, 3], dtype='float64') >>> x = paddle.to_tensor([8, 6, 4], dtype='float64') >>> paddle.cumulative_trapezoid(y, x) Tensor(shape=[2], dtype=float64, place=Place(cpu), stop_gradient=True, [-3., -8.]) >>> y = paddle.arange(6).reshape((2, 3)).astype('float32') >>> paddle.cumulative_trapezoid(y, axis=0) Tensor(shape=[1, 3], dtype=float32, place=Place(cpu), stop_gradient=True, [[1.50000000, 2.50000000, 3.50000000]]) >>> paddle.cumulative_trapezoid(y, axis=1) Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True, [[0.50000000, 2. ], [3.50000000, 8. ]])
-
deg2rad
(
name: str | None = None
)
Tensor
deg2rad¶
-
Convert each of the elements of input x from degrees to angles in radians.
\[deg2rad(x)=\pi * x / 180\]- Parameters
-
x (Tensor) – An N-D Tensor, the data type is float32, float64, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
An N-D Tensor, the shape and data type is the same with input (The output data type is float32 when the input data type is int).
- Return type
-
out (Tensor)
Examples
>>> import paddle >>> x1 = paddle.to_tensor([180.0, -180.0, 360.0, -360.0, 90.0, -90.0]) >>> result1 = paddle.deg2rad(x1) >>> result1 Tensor(shape=[6], dtype=float32, place=Place(cpu), stop_gradient=True, [3.14159274, -3.14159274, 6.28318548, -6.28318548, 1.57079637, -1.57079637]) >>> x2 = paddle.to_tensor(180) >>> result2 = paddle.deg2rad(x2) >>> result2 Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 3.14159274)
-
diag
(
offset: int = 0,
padding_value: int = 0,
name: Optional[str] = None
)
Tensor
diag¶
-
If
xis a vector (1-D tensor), a 2-D square tensor with the elements ofxas the diagonal is returned.If
xis a matrix (2-D tensor), a 1-D tensor with the diagonal elements ofxis returned.The argument
offsetcontrols the diagonal offset:If
offset= 0, it is the main diagonal.If
offset> 0, it is superdiagonal.If
offset< 0, it is subdiagonal.- Parameters
-
x (Tensor) – The input tensor. Its shape is either 1-D or 2-D. Its data type should be float16, float32, float64, int32, int64, complex64, complex128.
offset (int, optional) – The diagonal offset. A positive value represents superdiagonal, 0 represents the main diagonal, and a negative value represents subdiagonal.
padding_value (int|float, optional) – Use this value to fill the area outside the specified diagonal band. Only takes effect when the input is a 1-D Tensor. The default value is 0.
name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Returns
-
Tensor, a square matrix or a vector. The output data type is the same as input data type.
Examples
>>> import paddle >>> paddle.disable_static() >>> x = paddle.to_tensor([1, 2, 3]) >>> y = paddle.diag(x) >>> print(y) Tensor(shape=[3, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[1, 0, 0], [0, 2, 0], [0, 0, 3]]) >>> y = paddle.diag(x, offset=1) >>> print(y) Tensor(shape=[4, 4], dtype=int64, place=Place(cpu), stop_gradient=True, [[0, 1, 0, 0], [0, 0, 2, 0], [0, 0, 0, 3], [0, 0, 0, 0]]) >>> y = paddle.diag(x, padding_value=6) >>> print(y) Tensor(shape=[3, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[1, 6, 6], [6, 2, 6], [6, 6, 3]])
>>> import paddle >>> paddle.disable_static() >>> x = paddle.to_tensor([[1, 2, 3], [4, 5, 6]]) >>> y = paddle.diag(x) >>> print(y) Tensor(shape=[2], dtype=int64, place=Place(cpu), stop_gradient=True, [1, 5]) >>> y = paddle.diag(x, offset=1) >>> print(y) Tensor(shape=[2], dtype=int64, place=Place(cpu), stop_gradient=True, [2, 6]) >>> y = paddle.diag(x, offset=-1) >>> print(y) Tensor(shape=[1], dtype=int64, place=Place(cpu), stop_gradient=True, [4])
-
diag_embed
(
offset: int = 0,
dim1: int = -2,
dim2: int = -1
)
paddle.Tensor
diag_embed¶
-
Creates a tensor whose diagonals of certain 2D planes (specified by dim1 and dim2) are filled by
input. By default, a 2D plane formed by the last two dimensions of the returned tensor will be selected.The argument
offsetdetermines which diagonal is generated:If offset = 0, it is the main diagonal.
If offset > 0, it is above the main diagonal.
If offset < 0, it is below the main diagonal.
- Parameters
-
input (Tensor|numpy.ndarray) – The input tensor. Must be at least 1-dimensional. The input data type should be float32, float64, int32, int64.
offset (int, optional) – Which diagonal to consider. Default: 0 (main diagonal).
dim1 (int, optional) – The first dimension with respect to which to take diagonal. Default: -2.
dim2 (int, optional) – The second dimension with respect to which to take diagonal. Default: -1.
- Returns
-
Tensor, the output data type is the same as input data type.
Examples
>>> import paddle >>> diag_embed_input = paddle.arange(6) >>> diag_embed_output1 = paddle.diag_embed(diag_embed_input) >>> print(diag_embed_output1) Tensor(shape=[6, 6], dtype=int64, place=Place(cpu), stop_gradient=True, [[0, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0], [0, 0, 2, 0, 0, 0], [0, 0, 0, 3, 0, 0], [0, 0, 0, 0, 4, 0], [0, 0, 0, 0, 0, 5]]) >>> diag_embed_output2 = paddle.diag_embed(diag_embed_input, offset=-1, dim1=0,dim2=1 ) >>> print(diag_embed_output2) Tensor(shape=[7, 7], dtype=int64, place=Place(cpu), stop_gradient=True, [[0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0, 0], [0, 0, 2, 0, 0, 0, 0], [0, 0, 0, 3, 0, 0, 0], [0, 0, 0, 0, 4, 0, 0], [0, 0, 0, 0, 0, 5, 0]]) >>> diag_embed_input_2dim = paddle.reshape(diag_embed_input,[2,3]) >>> print(diag_embed_input_2dim) Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[0, 1, 2], [3, 4, 5]]) >>> diag_embed_output3 = paddle.diag_embed(diag_embed_input_2dim,offset= 0, dim1=0, dim2=2 ) >>> print(diag_embed_output3) Tensor(shape=[3, 2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[[0, 0, 0], [3, 0, 0]], [[0, 1, 0], [0, 4, 0]], [[0, 0, 2], [0, 0, 5]]])
-
diagflat
(
offset: int = 0,
name: Optional[str] = None
)
Tensor
diagflat¶
-
If
xis a vector (1-D tensor), a 2-D square tensor with the elements ofxas the diagonal is returned.If
xis a tensor (more than 1-D), a 2-D square tensor with the elements of flattenedxas the diagonal is returned.The argument
offsetcontrols the diagonal offset.If
offset= 0, it is the main diagonal.If
offset> 0, it is superdiagonal.If
offset< 0, it is subdiagonal.- Parameters
-
x (Tensor) – The input tensor. It can be any shape. Its data type should be float16, float32, float64, int32, int64.
offset (int, optional) – The diagonal offset. A positive value represents superdiagonal, 0 represents the main diagonal, and a negative value represents subdiagonal. Default: 0 (main diagonal).
name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Returns
-
Tensor, a square matrix. The output data type is the same as input data type.
Examples
>>> import paddle >>> x = paddle.to_tensor([1, 2, 3]) >>> y = paddle.diagflat(x) >>> print(y) Tensor(shape=[3, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[1, 0, 0], [0, 2, 0], [0, 0, 3]]) >>> y = paddle.diagflat(x, offset=1) >>> print(y) Tensor(shape=[4, 4], dtype=int64, place=Place(cpu), stop_gradient=True, [[0, 1, 0, 0], [0, 0, 2, 0], [0, 0, 0, 3], [0, 0, 0, 0]]) >>> y = paddle.diagflat(x, offset=-1) >>> print(y) Tensor(shape=[4, 4], dtype=int64, place=Place(cpu), stop_gradient=True, [[0, 0, 0, 0], [1, 0, 0, 0], [0, 2, 0, 0], [0, 0, 3, 0]])
>>> import paddle >>> x = paddle.to_tensor([[1, 2], [3, 4]]) >>> y = paddle.diagflat(x) >>> print(y) Tensor(shape=[4, 4], dtype=int64, place=Place(cpu), stop_gradient=True, [[1, 0, 0, 0], [0, 2, 0, 0], [0, 0, 3, 0], [0, 0, 0, 4]]) >>> y = paddle.diagflat(x, offset=1) >>> print(y) Tensor(shape=[5, 5], dtype=int64, place=Place(cpu), stop_gradient=True, [[0, 1, 0, 0, 0], [0, 0, 2, 0, 0], [0, 0, 0, 3, 0], [0, 0, 0, 0, 4], [0, 0, 0, 0, 0]]) >>> y = paddle.diagflat(x, offset=-1) >>> print(y) Tensor(shape=[5, 5], dtype=int64, place=Place(cpu), stop_gradient=True, [[0, 0, 0, 0, 0], [1, 0, 0, 0, 0], [0, 2, 0, 0, 0], [0, 0, 3, 0, 0], [0, 0, 0, 4, 0]])
-
diagonal
(
offset: int = 0,
axis1: int = 0,
axis2: int = 1,
name: str | None = None
)
Tensor
diagonal¶
-
Computes the diagonals of the input tensor x.
If
xis 2D, returns the diagonal. Ifxhas larger dimensions, diagonals be taken from the 2D planes specified by axis1 and axis2. By default, the 2D planes formed by the first and second axis of the input tensor x.The argument
offsetdetermines where diagonals are taken from input tensor x:If offset = 0, it is the main diagonal.
If offset > 0, it is above the main diagonal.
If offset < 0, it is below the main diagonal.
- Parameters
-
x (Tensor) – The input tensor x. Must be at least 2-dimensional. The input data type should be bool, int32, int64, bfloat16, float16, float32, float64.
offset (int, optional) – Which diagonals in input tensor x will be taken. Default: 0 (main diagonals).
axis1 (int, optional) – The first axis with respect to take diagonal. Default: 0.
axis2 (int, optional) – The second axis with respect to take diagonal. Default: 1.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
a partial view of input tensor in specify two dimensions, the output data type is the same as input data type.
- Return type
-
Tensor
Examples
>>> import paddle >>> paddle.seed(2023) >>> x = paddle.rand([2, 2, 3],'float32') >>> print(x) Tensor(shape=[2, 2, 3], dtype=float32, place=Place(cpu), stop_gradient=True, [[[0.86583614, 0.52014720, 0.25960937], [0.90525323, 0.42400089, 0.40641287]], [[0.97020894, 0.74437362, 0.51785129], [0.73292869, 0.97786582, 0.04315904]]]) >>> out1 = paddle.diagonal(x) >>> print(out1) Tensor(shape=[3, 2], dtype=float32, place=Place(cpu), stop_gradient=True, [[0.86583614, 0.73292869], [0.52014720, 0.97786582], [0.25960937, 0.04315904]]) >>> out2 = paddle.diagonal(x, offset=0, axis1=2, axis2=1) >>> print(out2) Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True, [[0.86583614, 0.42400089], [0.97020894, 0.97786582]]) >>> out3 = paddle.diagonal(x, offset=1, axis1=0, axis2=1) >>> print(out3) Tensor(shape=[3, 1], dtype=float32, place=Place(cpu), stop_gradient=True, [[0.90525323], [0.42400089], [0.40641287]]) >>> out4 = paddle.diagonal(x, offset=0, axis1=1, axis2=2) >>> print(out4) Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True, [[0.86583614, 0.42400089], [0.97020894, 0.97786582]])
-
diagonal_scatter
(
y: Tensor,
offset: int = 0,
axis1: int = 0,
axis2: int = 1,
name: str | None = None
)
Tensor
diagonal_scatter¶
-
Embed the values of Tensor
yinto Tensorxalong the diagonal elements of Tensorx, with respect toaxis1andaxis2.This function returns a tensor with fresh storage.
The argument
offsetcontrols which diagonal to consider:If
offset= 0, it is the main diagonal.If
offset> 0, it is above the main diagonal.If
offset< 0, it is below the main diagonal.
Note
yshould have the same shape as paddle.diagonal.The image below demonstrates the example: A 2D tensor with a shape of [2, 3] is
diagonal_scatteralong its main diagonal (offset = 0) withinaxis1 = 0andaxis2 = 1using a 1D tensor filled with ones.
- Parameters
-
x (Tensor) –
xis the original Tensor. Must be at least 2-dimensional.y (Tensor) –
yis the Tensor to embed intoxoffset (int, optional) – which diagonal to consider. Default: 0 (main diagonal).
axis1 (int, optional) – first axis with respect to which to take diagonal. Default: 0.
axis2 (int, optional) – second axis with respect to which to take diagonal. Default: 1.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, Tensor with diagonal embedded with
y.
Examples
>>> import paddle >>> x = paddle.arange(6.0).reshape((2, 3)) >>> y = paddle.ones((2,)) >>> out = x.diagonal_scatter(y) >>> print(out) Tensor(shape=[2, 3], dtype=float32, place=Place(gpu:0), stop_gradient=True, [[1., 1., 2.], [3., 1., 5.]])
-
diff
(
n: int = 1,
axis: int = -1,
prepend: Tensor | None = None,
append: Tensor | None = None,
name: str | None = None,
*,
out: Tensor | None = None
)
Tensor
diff¶
-
Computes the n-th forward difference along the given axis. The first-order differences is computed by using the following formula:
\[out[i] = x[i+1] - x[i]\]Higher-order differences are computed by using paddle.diff() recursively. The number of n supports any positive integer value.
Note
Alias Support: The parameter name
inputcan be used as an alias forx, anddimcan be used as an alias foraxis. For example,diff(input=tensor_x, dim=1, ...)is equivalent todiff(x=tensor_x, axis=1, ...).- Parameters
-
x (Tensor) – The input tensor to compute the forward difference on, the data type is float16, float32, float64, bool, int32, int64. alias:
input.n (int, optional) – The number of times to recursively compute the difference. Supports any positive integer value. Default:1
axis (int, optional) – The axis to compute the difference along. Default:-1 alias:
dim.prepend (Tensor|None, optional) – The tensor to prepend to input along axis before computing the difference. It’s dimensions must be equivalent to that of x, and its shapes must match x’s shape except on axis.
append (Tensor|None, optional) – The tensor to append to input along axis before computing the difference, It’s dimensions must be equivalent to that of x, and its shapes must match x’s shape except on axis.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
out (Tensor, optional) – The output tensor. If provided, the result will be stored in this tensor.
- Returns
-
The output tensor with same dtype with x.
- Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.to_tensor([1, 4, 5, 2]) >>> out = paddle.diff(x) >>> out Tensor(shape=[3], dtype=int64, place=Place(cpu), stop_gradient=True, [ 3, 1, -3]) >>> x_2 = paddle.to_tensor([1, 4, 5, 2]) >>> out = paddle.diff(x_2, n=2) >>> out Tensor(shape=[2], dtype=int64, place=Place(cpu), stop_gradient=True, [ -2, -4]) >>> y = paddle.to_tensor([7, 9]) >>> out = paddle.diff(x, append=y) >>> out Tensor(shape=[5], dtype=int64, place=Place(cpu), stop_gradient=True, [ 3, 1, -3, 5, 2]) >>> out = paddle.diff(x, n=2, append=y) >>> out Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True, [-2, -4, 8, -3]) >>> out = paddle.diff(x, n=3, append=y) >>> out Tensor(shape=[3], dtype=int64, place=Place(cpu), stop_gradient=True, [-2 , 12, -11]) >>> z = paddle.to_tensor([[1, 2, 3], [4, 5, 6]]) >>> out = paddle.diff(z, axis=0) >>> out Tensor(shape=[1, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[3, 3, 3]]) >>> out = paddle.diff(z, axis=1) >>> out Tensor(shape=[2, 2], dtype=int64, place=Place(cpu), stop_gradient=True, [[1, 1], [1, 1]])
-
digamma
(
name: str | None = None
)
Tensor
digamma¶
-
Calculates the digamma of the given input tensor, element-wise.
\[Out = \Psi(x) = \frac{ \Gamma^{'}(x) }{ \Gamma(x) }\]- Parameters
-
x (Tensor) – Input Tensor. Must be one of the following types: bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
- Tensor, the digamma of the input Tensor, the shape and data type is the same with input
-
(integer types are autocasted into float32).
Examples
>>> import paddle >>> data = paddle.to_tensor([[1, 1.5], [0, -2.2]], dtype='float32') >>> res = paddle.digamma(data) >>> res Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True, [[-0.57721591, 0.03648996], [ nan , 5.32286835]])
-
digamma_
(
name: str | None = None
)
Tensor
digamma_¶
-
Inplace version of
digammaAPI, the output Tensor will be inplaced with inputx. Please refer to digamma.
-
dim
(
)
dim¶
-
Returns the dimension of current Variable
- Returns
-
the dimension
Examples
>>> import paddle >>> paddle.enable_static() >>> # create a static Variable >>> x = paddle.static.data(name='x', shape=[3, 2, 1]) >>> # print the dimension of the Variable >>> print(x.dim()) 3
-
dist
(
y: Tensor,
p: float = 2,
name: str | None = None
)
Tensor
dist¶
-
Returns the p-norm of (x - y). It is not a norm in a strict sense, only as a measure of distance. The shapes of x and y must be broadcastable. The definition is as follows, for details, please refer to the Introduction to Tensor:
Each input has at least one dimension.
Match the two input dimensions from back to front, the dimension sizes must either be equal, one of them is 1, or one of them does not exist.
Where, z = x - y, the shapes of x and y are broadcastable, then the shape of z can be obtained as follows:
1. If the number of dimensions of x and y are not equal, prepend 1 to the dimensions of the tensor with fewer dimensions.
For example, The shape of x is [8, 1, 6, 1], the shape of y is [7, 1, 5], prepend 1 to the dimension of y.
x (4-D Tensor): 8 x 1 x 6 x 1
y (4-D Tensor): 1 x 7 x 1 x 5
2. Determine the size of each dimension of the output z: choose the maximum value from the two input dimensions.
z (4-D Tensor): 8 x 7 x 6 x 5
If the number of dimensions of the two inputs are the same, the size of the output can be directly determined in step 2. When p takes different values, the norm formula is as follows:
When p = 0, defining $0^0=0$, the zero-norm of z is simply the number of non-zero elements of z.
\[\begin{split}||z||_{0}=\lim_{p \\rightarrow 0}\sum_{i=1}^{m}|z_i|^{p}\end{split}\]When p = inf, the inf-norm of z is the maximum element of the absolute value of z.
\[||z||_\infty=\max_i |z_i|\]When p = -inf, the negative-inf-norm of z is the minimum element of the absolute value of z.
\[||z||_{-\infty}=\min_i |z_i|\]Otherwise, the p-norm of z follows the formula,
\[\begin{split}||z||_{p}=(\sum_{i=1}^{m}|z_i|^p)^{\\frac{1}{p}}\end{split}\]- Parameters
-
x (Tensor) – 1-D to 6-D Tensor, its data type is bfloat16, float16, float32 or float64.
y (Tensor) – 1-D to 6-D Tensor, its data type is bfloat16, float16, float32 or float64.
p (float, optional) – The norm to be computed, its data type is float32 or float64. Default: 2.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
- Returns
-
Tensor that is the p-norm of (x - y).
- Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.to_tensor([[3, 3],[3, 3]], dtype="float32") >>> y = paddle.to_tensor([[3, 3],[3, 1]], dtype="float32") >>> out = paddle.dist(x, y, 0) >>> print(out) Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 1.) >>> out = paddle.dist(x, y, 2) >>> print(out) Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 2.) >>> out = paddle.dist(x, y, float("inf")) >>> print(out) Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 2.) >>> out = paddle.dist(x, y, float("-inf")) >>> print(out) Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 0.)
-
div
(
y: Tensor,
name: str | None = None,
*,
rounding_mode: str | None = None,
out: Tensor | None = None
)
Tensor
div¶
-
Divide two tensors element-wise. The equation is:
\[out = x / y\]Note
paddle.dividesupports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .Note
Alias Support: The parameter name
inputcan be used as an alias forx, andothercan be used as an alias fory. For example,divide(input=tensor_x, other=tensor_y)is equivalent todivide(x=tensor_x, y=tensor_y).- Parameters
-
x (Tensor) – the input tensor, it’s data type should be bool, bfloat16, float16, float32, float64, int8, int16, int32, int64, uint8, complex64, complex128. alias:
input.y (Tensor) – the input tensor, it’s data type should be bool, bfloat16, float16, float32, float64, int8, int16, int32, int64, uint8, complex64, complex128. alias:
other.rounding_mode (str|None, optional) – The rounding mode. Can be None (default), “trunc” (truncate toward zero), or “floor” (round down toward negative infinity).
out (Tensor, optional) – The output tensor. Default: None.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
N-D Tensor. A location into which the result is stored. If x, y have different shapes and are “broadcastable”, the resulting tensor shape is the shape of x and y after broadcasting. If x, y have the same shape, its shape is the same as x and y.
Examples
>>> import paddle >>> x = paddle.to_tensor([2, 3, 4], dtype='float64') >>> y = paddle.to_tensor([1, 5, 2], dtype='float64') >>> z = paddle.divide(x, y) >>> print(z) Tensor(shape=[3], dtype=float64, place=Place(cpu), stop_gradient=True, [2. , 0.60000000, 2. ])
-
div_
(
y: Tensor,
name: str | None = None,
*,
rounding_mode: str | None = None
)
Tensor
div_¶
-
Inplace version of
divideAPI, the output Tensor will be inplaced with inputx. Please refer to api_paddle_divide.
-
divide
(
y: Tensor,
name: str | None = None,
*,
rounding_mode: str | None = None,
out: Tensor | None = None
)
Tensor
divide¶
-
Divide two tensors element-wise. The equation is:
\[out = x / y\]Note
paddle.dividesupports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .Note
Alias Support: The parameter name
inputcan be used as an alias forx, andothercan be used as an alias fory. For example,divide(input=tensor_x, other=tensor_y)is equivalent todivide(x=tensor_x, y=tensor_y).- Parameters
-
x (Tensor) – the input tensor, it’s data type should be bool, bfloat16, float16, float32, float64, int8, int16, int32, int64, uint8, complex64, complex128. alias:
input.y (Tensor) – the input tensor, it’s data type should be bool, bfloat16, float16, float32, float64, int8, int16, int32, int64, uint8, complex64, complex128. alias:
other.rounding_mode (str|None, optional) – The rounding mode. Can be None (default), “trunc” (truncate toward zero), or “floor” (round down toward negative infinity).
out (Tensor, optional) – The output tensor. Default: None.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
N-D Tensor. A location into which the result is stored. If x, y have different shapes and are “broadcastable”, the resulting tensor shape is the shape of x and y after broadcasting. If x, y have the same shape, its shape is the same as x and y.
Examples
>>> import paddle >>> x = paddle.to_tensor([2, 3, 4], dtype='float64') >>> y = paddle.to_tensor([1, 5, 2], dtype='float64') >>> z = paddle.divide(x, y) >>> print(z) Tensor(shape=[3], dtype=float64, place=Place(cpu), stop_gradient=True, [2. , 0.60000000, 2. ])
-
divide_
(
y: Tensor,
name: str | None = None,
*,
rounding_mode: str | None = None
)
Tensor
divide_¶
-
Inplace version of
divideAPI, the output Tensor will be inplaced with inputx. Please refer to api_paddle_divide.
-
dot
(
y: Tensor,
name: str | None = None
)
Tensor
dot¶
-
This operator calculates inner product for vectors.
Note
Support 1-d and 2-d Tensor. When it is 2d, the first dimension of this matrix is the batch dimension, which means that the vectors of multiple batches are dotted.
- Parameters
-
x (Tensor) – 1-D or 2-D
Tensor. Its dtype should befloat32,float64,int32,int64,complex64,complex128y (Tensor) – 1-D or 2-D
Tensor. Its dtype should befloat32,float64,int32,int64,complex64,complex128name (str|None, optional) – Name of the output. Default is None. It’s used to print debug info for developers. Details: api_guide_Name
- Returns
-
the calculated result Tensor.
- Return type
-
Tensor
Examples
>>> import paddle >>> # 1-D Tensor * 1-D Tensor >>> x = paddle.to_tensor([1, 2, 3]) >>> y = paddle.to_tensor([4, 5, 6]) >>> z = paddle.dot(x, y) >>> print(z) Tensor(shape=[], dtype=int64, place=Place(cpu), stop_gradient=True, 32) >>> # 2-D Tensor * 2-D Tensor >>> x = paddle.to_tensor([[1, 2, 3], [2, 4, 6]]) >>> y = paddle.to_tensor([[4, 5, 6], [4, 5, 6]]) >>> z = paddle.dot(x, y) >>> print(z) Tensor(shape=[2], dtype=int64, place=Place(cpu), stop_gradient=True, [32, 64])
-
dsplit
(
num_or_indices: int | Sequence[int],
name: str | None = None
)
list[Tensor]
dsplit¶
-
dsplitFull name Depth Split, splits the input Tensor into multiple sub-Tensors along the depth axis, which is equivalent topaddle.tensor_splitwithaxis=2.Note
Make sure that the number of Tensor dimensions transformed using
paddle.dsplitmust be no less than 3.In the following figure, Tenser
xhas shape [4, 4, 4], and afterpaddle.dsplit(x, num_or_indices=2)transformation, we getout0andout1sub-Tensors whose shapes are both [4, 4, 2] :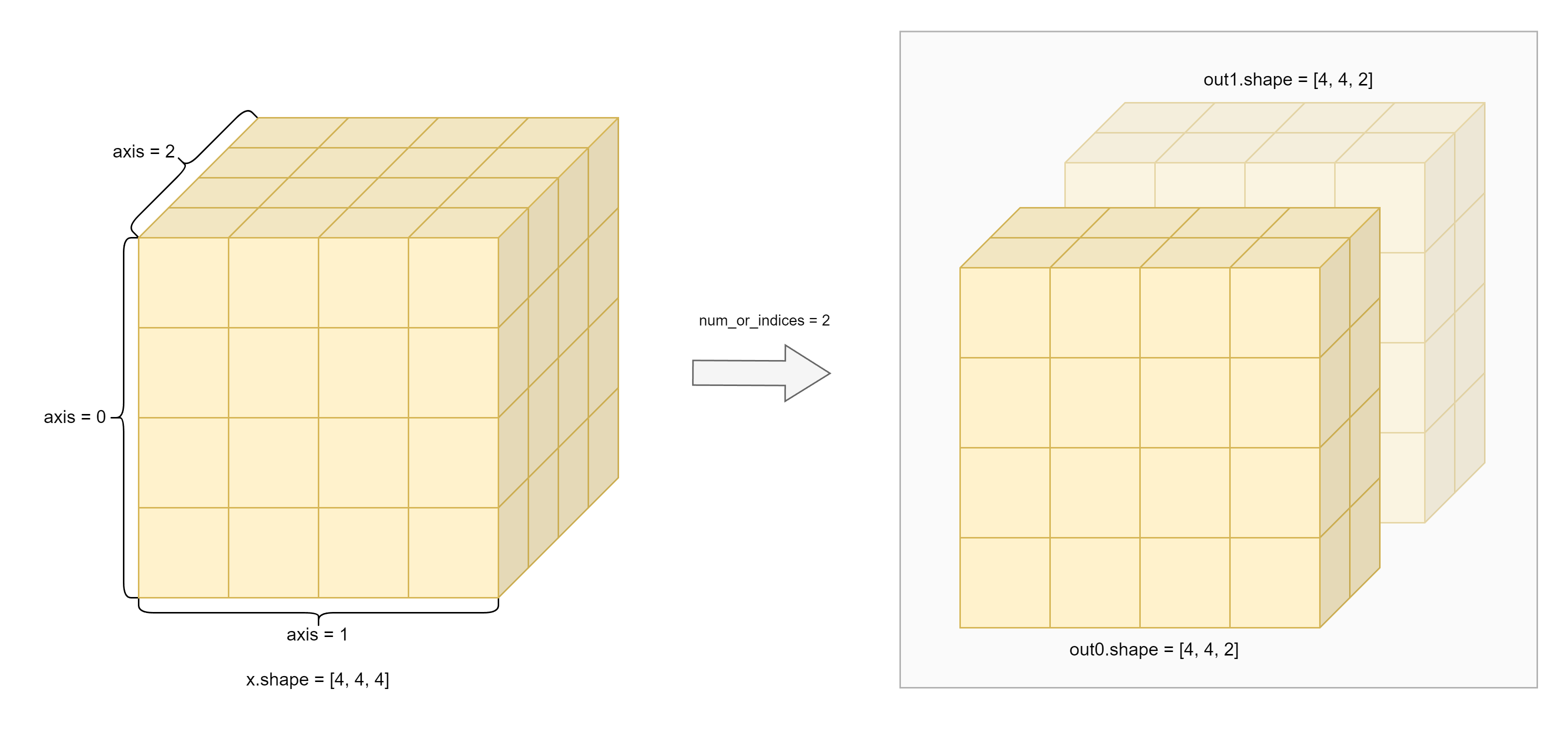
- Parameters
-
x (Tensor) – A Tensor whose dimension must be greater than 2. The data type is bool, bfloat16, float16, float32, float64, uint8, int32 or int64.
num_or_indices (int|list|tuple) – If
num_or_indicesis an intn,xis split intonsections. Ifnum_or_indicesis a list or tuple of integer indices,xis split at each of the indices.name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name .
- Returns
-
list[Tensor], The list of segmented Tensors.
Examples
>>> import paddle >>> # x is a Tensor of shape [7, 6, 8] >>> x = paddle.rand([7, 6, 8]) >>> out0, out1 = paddle.dsplit(x, num_or_indices=2) >>> print(out0.shape) [7, 6, 4] >>> print(out1.shape) [7, 6, 4] >>> out0, out1, out2 = paddle.dsplit(x, num_or_indices=[1, 4]) >>> print(out0.shape) [7, 6, 1] >>> print(out1.shape) [7, 6, 3] >>> print(out2.shape) [7, 6, 4]
-
eig
(
name: str | None = None
)
tuple[Tensor, Tensor]
eig¶
-
Performs the eigenvalue decomposition of a square matrix or a batch of square matrices.
Note
If the matrix is a Hermitian or a real symmetric matrix, please use eigh instead, which is much faster.
If only eigenvalues is needed, please use eigvals instead.
If the matrix is of any shape, please use svd.
This API is only supported on CPU device.
The output datatype is always complex for both real and complex input.
- Parameters
-
x (Tensor) – A tensor with shape math:[*, N, N], The data type of the x should be one of
float32,float64,complex64orcomplex128.name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
- Returns
-
A tensor with shape math:[*, N] refers to the eigen values. Eigenvectors(Tensor): A tensor with shape math:[*, N, N] refers to the eigen vectors.
- Return type
-
Eigenvalues(Tensor)
Examples
>>> import paddle >>> x = paddle.to_tensor([[1.6707249, 7.2249975, 6.5045543], ... [9.956216, 8.749598, 6.066444 ], ... [4.4251957, 1.7983172, 0.370647 ]]) >>> w, v = paddle.linalg.eig(x) >>> print(v) Tensor(shape=[3, 3], dtype=complex64, place=Place(cpu), stop_gradient=True, [[ (0.5061365365982056+0j) , (0.7971761226654053+0j) , (0.1851806491613388+0j) ], [ (0.8308236598968506+0j) , (-0.3463813066482544+0j) , (-0.6837005615234375+0j) ], [ (0.23142573237419128+0j), (-0.49449989199638367+0j), (0.7058765292167664+0j) ]]) >>> print(w) Tensor(shape=[3], dtype=complex64, place=Place(cpu), stop_gradient=True, [ (16.50470733642578+0j) , (-5.503481388092041+0j) , (-0.21026138961315155+0j)])
-
eigvals
(
name: str | None = None
)
Tensor
eigvals¶
-
Compute the eigenvalues of one or more general matrices.
Warning
The gradient kernel of this operator does not yet developed. If you need back propagation through this operator, please replace it with paddle.linalg.eig.
- Parameters
-
x (Tensor) – A square matrix or a batch of square matrices whose eigenvalues will be computed. Its shape should be [*, M, M], where * is zero or more batch dimensions. Its data type should be float32, float64, complex64, or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, A tensor containing the unsorted eigenvalues which has the same batch dimensions with x. The eigenvalues are complex-valued even when x is real.
Examples
>>> import paddle >>> paddle.seed(2023) >>> x = paddle.rand(shape=[3, 3], dtype='float64') >>> print(x) Tensor(shape=[3, 3], dtype=float64, place=Place(cpu), stop_gradient=True, [[0.86583615, 0.52014721, 0.25960938], [0.90525323, 0.42400090, 0.40641288], [0.97020893, 0.74437359, 0.51785128]]) >>> print(paddle.linalg.eigvals(x)) Tensor(shape=[3], dtype=complex128, place=Place(cpu), stop_gradient=True, [ (1.788956694280852+0j) , (0.16364484879581526+0j), (-0.14491322408727625+0j)])
-
eigvalsh
(
UPLO: Literal['L', 'U'] = 'L',
name: str | None = None
)
Tensor
eigvalsh¶
-
Computes the eigenvalues of a complex Hermitian (conjugate symmetric) or a real symmetric matrix.
- Parameters
-
x (Tensor) – A tensor with shape \([*, M, M]\) , where * is zero or greater batch dimension. The data type of the input Tensor x should be one of float32, float64, complex64, complex128.
UPLO (str, optional) – Lower triangular part of a (‘L’, default) or the upper triangular part (‘U’).
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
- Returns
-
The tensor eigenvalues in ascending order.
- Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.to_tensor([[1, -2j], [2j, 5]]) >>> out_value = paddle.eigvalsh(x, UPLO='L') >>> print(out_value) Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True, [0.17157286, 5.82842731])
-
equal
(
y: Tensor,
name: str | None = None,
*,
out: Tensor | None = None
)
Tensor
equal¶
-
This layer returns the truth value of \(x == y\) elementwise.
Note
The output has no gradient.
- Parameters
-
x (Tensor) – Tensor, data type is bool, float16, float32, float64, uint8, int8, int16, int32, int64, complex64, complex128. alias:
inputy (Tensor) – Tensor, data type is bool, float16, float32, float64, uint8, int8, int16, int32, int64, complex64, complex128. alias:
othername (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
out (Tensor, optional) – Output tensor. If provided, the result will be stored in this tensor.
- Returns
-
output Tensor, it’s shape is the same as the input’s Tensor, and the data type is bool. The result of this op is stop_gradient.
- Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.to_tensor([1, 2, 3]) >>> y = paddle.to_tensor([1, 3, 2]) >>> result1 = paddle.equal(x, y) >>> print(result1) Tensor(shape=[3], dtype=bool, place=Place(cpu), stop_gradient=True, [True , False, False])
-
equal_
(
y: Tensor,
name: str | None = None
)
Tensor
equal_¶
-
Inplace version of
equalAPI, the output Tensor will be inplaced with inputx. Please refer to api_paddle_equal.
-
equal_all
(
y: Tensor,
name: str | None = None
)
Tensor
equal_all¶
-
Returns the truth value of \(x == y\). True if two inputs have the same elements, False otherwise.
Note
The output has no gradient.
- Parameters
-
x (Tensor) – Tensor, data type is bool, float32, float64, int32, int64.
y (Tensor) – Tensor, data type is bool, float32, float64, int32, int64.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
- Returns
-
output Tensor, data type is bool, value is [False] or [True].
- Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.to_tensor([1, 2, 3]) >>> y = paddle.to_tensor([1, 2, 3]) >>> z = paddle.to_tensor([1, 4, 3]) >>> result1 = paddle.equal_all(x, y) >>> print(result1) Tensor(shape=[], dtype=bool, place=Place(cpu), stop_gradient=True, True) >>> result2 = paddle.equal_all(x, z) >>> print(result2) Tensor(shape=[], dtype=bool, place=Place(cpu), stop_gradient=True, False)
-
erf
(
name: str | None = None
)
Tensor
erf¶
-
The error function. For more details, see Error function.
- Equation:
-
\[out = \frac{2}{\sqrt{\pi}} \int_{0}^{x}e^{- \eta^{2}}d\eta\]
- Parameters
-
x (Tensor) – The input tensor, it’s data type should be float32, float64, uint8, int8, int16, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
float32 or float64 (integer types are autocasted into float32), shape: the same as the input.
- Return type
-
Tensor. The output of Erf, dtype
Examples
>>> import paddle >>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3]) >>> out = paddle.erf(x) >>> print(out) Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [-0.42839241, -0.22270259, 0.11246292, 0.32862678])
-
erfinv
(
name: str | None = None
)
Tensor
erfinv¶
-
The inverse error function of x. Please refer to erf
\[erfinv(erf(x)) = x.\]- Parameters
-
x (Tensor) – An N-D Tensor, the data type is float16, bfloat16, float32, float64, uint8, int8, int16, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
- out (Tensor), an N-D Tensor, the shape and data type is the same with input
-
(integer types are autocasted into float32).
Example
>>> import paddle >>> x = paddle.to_tensor([0, 0.5, -1.], dtype="float32") >>> out = paddle.erfinv(x) >>> out Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True, [ 0. , 0.47693631, -inf. ])
-
erfinv_
(
name: str | None = None
)
Tensor
erfinv_¶
-
Inplace version of
erfinvAPI, the output Tensor will be inplaced with inputx. Please refer to erfinv.
-
exp
(
name: str | None = None
)
Tensor
exp¶
-
Computes exp of x element-wise with a natural number e as the base.
\[out = e^x\]- Parameters
-
x (Tensor) – Input of Exp operator, an N-D Tensor, with data type int32, int64, bfloat16, float16, float32, float64, complex64 or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor. Output of Exp operator, a Tensor with shape same as input.
Examples
>>> import paddle >>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3]) >>> out = paddle.exp(x) >>> print(out) Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [0.67032003, 0.81873077, 1.10517097, 1.34985888])
-
exp_
(
name=None
)
exp_¶
-
Inplace version of
expAPI, the output Tensor will be inplaced with inputx. Please refer to exp.
-
expand
(
shape: ShapeLike,
name: str | None = None
)
Tensor
expand¶
-
Expand the input tensor to a given shape.
Both the number of dimensions of
xand the number of elements inshapeshould be less than or equal to 6. And the number of dimensions ofxshould be less than the number of elements inshape. The dimension to expand must have a value 0.The image illustrates a typical case of the expand operation. The Original Tensor is a 1D tensor with shape
[3]and values [1, 2, 3]. Using thepaddle.expandmethod with the parametershape = [2, 3], it is broadcasted and expanded into a 2D tensor with shape[2, 3]
Note
Alias Support: The parameter name
inputcan be used as an alias forxandsizecan be used as an alias forshape.shapecan be a variable number of arguments. For example:paddle.expand(tensor_x, shape=[3, 4], name=None)tensor_x.expand([3, 4]) -> paddle.expand(tensor_x, [3, 4])tensor_x.expand(3, 4) -> paddle.expand(tensor_x, 3, 4)tensor_x.expand(size=[3, 4]) -> paddle.expand(tensor_x, size=[3, 4])- Parameters
-
x (Tensor) – The input Tensor, its data type is bool, float16, float32, float64, int32, int64, uint8, uint16, complex64 or complex128. alias:
inputshape (list|tuple|Tensor|variable number of arguments) – The result shape after expanding. The data type is int32. If shape is a list or tuple, all its elements should be integers or 0-D or 1-D Tensors with the data type int32. If shape is a Tensor, it should be an 1-D Tensor with the data type int32. The value -1 in shape means keeping the corresponding dimension unchanged.
shapecan be a variable number of arguments. alias:size.name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name .
- Returns
-
N-D Tensor, A Tensor with the given shape. The data type is the same as
x.
Examples
>>> import paddle >>> data = paddle.to_tensor([1, 2, 3], dtype='int32') >>> out = paddle.expand(data, shape=[2, 3]) >>> print(out) Tensor(shape=[2, 3], dtype=int32, place=Place(cpu), stop_gradient=True, [[1, 2, 3], [1, 2, 3]])
-
expand_as
(
)
expand_as¶
-
C++ interface function for expand_as.
-
expm1
(
name: str | None = None
)
Tensor
expm1¶
-
Expm1 Operator. Computes expm1 of x element-wise with a natural number \(e\) as the base.
\[out = e^x - 1\]- Parameters
-
x (Tensor) – Input of Expm1 operator, an N-D Tensor, with data type int32, int64, bfloat16, float16, float32, float64, complex64 or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor. Output of Expm1 operator, a Tensor with shape same as input.
Examples
>>> import paddle >>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3]) >>> out = paddle.expm1(x) >>> print(out) Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [-0.32967997, -0.18126924, 0.10517092, 0.34985882])
-
exponential_
(
lam: float = 1.0,
name: str | None = None
)
Tensor
exponential_¶
-
This inplace OP fill input Tensor
xwith random number from a Exponential Distribution.lamis \(\lambda\) parameter of Exponential Distribution.\[f(x) = \lambda e^{-\lambda x}\]Note
Alias Support: The parameter name
lambdcan be used as an alias forlam. For example,exponential_(tensor_x, lambd=1.0, ...)is equivalent toexponential_(tensor_x, lam=1.0, ...).- Parameters
-
x (Tensor) – Input tensor. The data type should be float32, float64.
lam (float, optional) – \(\lambda\) parameter of Exponential Distribution. Default, 1.0. alias:
lambd.name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
- Returns
-
Tensor, Input Tensor
x.
Examples
>>> import paddle >>> paddle.set_device('cpu') >>> paddle.seed(100) >>> x = paddle.empty([2,3]) >>> x.exponential_() >>> Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True, [[0.80643415, 0.23211166, 0.01169797], [0.72520679, 0.45208144, 0.30234432]]) >>>
-
flatten
(
start_axis: int = 0,
stop_axis: int = -1,
name: str | None = None
)
Tensor
flatten¶
-
Flattens a contiguous range of axes in a tensor according to start_axis and stop_axis.
Note
The output Tensor will share data with origin Tensor and doesn’t have a Tensor copy in
dygraphmode. If you want to use the Tensor copy version, please use Tensor.clone likeflatten_clone_x = x.flatten().clone().For Example:
Case 1: Given X.shape = (3, 100, 100, 4) and start_axis = 1 end_axis = 2 We get: Out.shape = (3, 100 * 100, 4) Case 2: Given X.shape = (3, 100, 100, 4) and start_axis = 0 stop_axis = -1 We get: Out.shape = (3 * 100 * 100 * 4)Note
Alias Support: The parameter name
inputcan be used as an alias forx, the parameter namestart_dimcan be used as an alias forstart_axis, and the parameter nameend_dimcan be used as an alias forstop_axis. For example,flatten(input=tensor_x, start_dim=0, end_dim=-1)is equivalent toflatten(x=tensor_x, start_axis=0, stop_axis=-1).- Parameters
-
x (Tensor) –
- A tensor of number of dimensions >= axis. A tensor with data type float16, float32,
-
float64, int8, int32, int64, uint8.
alias:
input.start_axis (int) – the start axis to flatten alias:
start_dim.stop_axis (int) – the stop axis to flatten alias:
end_dim.name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, A tensor with the contents of the input tensor, whose input axes are flattened by indicated
start_axisandend_axis, and data type is the same as inputx.
Examples
>>> import paddle >>> image_shape=(2, 3, 4, 4) >>> x = paddle.arange(end=image_shape[0] * image_shape[1] * image_shape[2] * image_shape[3]) >>> img = paddle.reshape(x, image_shape) >>> out = paddle.flatten(img, start_axis=1, stop_axis=2) >>> print(out.shape) [2, 12, 4] >>> # out shares data with img in dygraph mode >>> img[0, 0, 0, 0] = -1 >>> print(out[0, 0, 0]) Tensor(shape=[], dtype=int64, place=Place(cpu), stop_gradient=True, -1)
-
flatten_
(
start_axis: int = 0,
stop_axis: int = -1,
name: str | None = None
)
Tensor
flatten_¶
-
Inplace version of
flattenAPI, the output Tensor will be inplaced with inputx. Please refer to flatten.
-
flip
(
axis: Sequence[int] | int,
name: str | None = None
)
Tensor
flip¶
-
Reverse the order of a n-D tensor along given axis in axis.
The image below illustrates how
flipworks.
- Parameters
-
x (Tensor) – A Tensor with shape \([N_1, N_2,..., N_k]\) . The data type of the input Tensor x should be float32, float64, int32, int64, bool.
axis (list|tuple|int) – The axis(axes) to flip on. Negative indices for indexing from the end are accepted.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, Tensor or DenseTensor calculated by flip layer. The data type is same with input x.
Examples
>>> >>> import paddle >>> image_shape=(3, 2, 2) >>> img = paddle.arange(image_shape[0] * image_shape[1] * image_shape[2]).reshape(image_shape) >>> tmp = paddle.flip(img, [0,1]) >>> print(tmp) Tensor(shape=[3, 2, 2], dtype=int64, place=Place(cpu), stop_gradient=True, [[[10, 11], [8 , 9 ]], [[6 , 7 ], [4 , 5 ]], [[2 , 3 ], [0 , 1 ]]]) >>> out = paddle.flip(tmp,-1) >>> print(out) Tensor(shape=[3, 2, 2], dtype=int64, place=Place(cpu), stop_gradient=True, [[[11, 10], [9 , 8 ]], [[7 , 6 ], [5 , 4 ]], [[3 , 2 ], [1 , 0 ]]])
-
floor
(
)
floor¶
-
C++ interface function for floor.
-
floor_
(
name=None
)
floor_¶
-
Inplace version of
floorAPI, the output Tensor will be inplaced with inputx. Please refer to floor.
-
floor_divide
(
y: Tensor,
name: str | None = None
)
Tensor
floor_divide¶
-
Floor divide two tensors element-wise and rounds the quotinents to the nearest integer toward negative infinite. The equation is:
\[out = floor(x / y)\]\(x\): Multidimensional Tensor.
\(y\): Multidimensional Tensor.
Note
paddle.floor_dividesupports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .- Parameters
-
x (Tensor) – the input tensor, it’s data type should be uint8, int8, int32, int64, float32, float64, float16, bfloat16.
y (Tensor) – the input tensor, it’s data type should be uint8, int8, int32, int64, float32, float64, float16, bfloat16.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
N-D Tensor. A location into which the result is stored. It’s dimension equals with $x$.
Examples
>>> import paddle >>> x = paddle.to_tensor([2, 3, 8, 7]) >>> y = paddle.to_tensor([1, 5, 3, 3]) >>> z = paddle.floor_divide(x, y) >>> print(z) Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True, [2, 0, 2, 2]) >>> x = paddle.to_tensor([2, 3, 8, 7]) >>> y = paddle.to_tensor([1, -5, -3, -3]) >>> z = paddle.floor_divide(x, y) >>> print(z) Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True, [2, -1, -3, -3])
-
floor_divide_
(
y: Tensor,
name: str | None = None
)
Tensor
floor_divide_¶
-
Inplace version of
floor_divideAPI, the output Tensor will be inplaced with inputx. Please refer to floor_divide.
-
floor_mod
(
y: Tensor,
name: str | None = None
)
Tensor
floor_mod¶
-
Mod two tensors element-wise. The equation is:
\[out = x \% y\]Note
paddle.remaindersupports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .And mod, floor_mod are all functions with the same name
- Parameters
-
x (Tensor) – the input tensor, it’s data type should be bfloat16, float16, float32, float64, int32, int64.
y (Tensor) – the input tensor, it’s data type should be bfloat16, float16, float32, float64, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
N-D Tensor. A location into which the result is stored. If x, y have different shapes and are “broadcastable”, the resulting tensor shape is the shape of x and y after broadcasting. If x, y have the same shape, its shape is the same as x and y.
Examples
>>> import paddle >>> x = paddle.to_tensor([2, 3, 8, 7]) >>> y = paddle.to_tensor([1, 5, 3, 3]) >>> z = paddle.remainder(x, y) >>> print(z) Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True, [0, 3, 2, 1]) >>> z = paddle.floor_mod(x, y) >>> print(z) Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True, [0, 3, 2, 1]) >>> z = paddle.mod(x, y) >>> print(z) Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True, [0, 3, 2, 1])
-
floor_mod_
(
y: Tensor,
name: str | None = None
)
Tensor
floor_mod_¶
-
Inplace version of
floor_mod_API, the output Tensor will be inplaced with inputx. Please refer to floor_mod_.
-
fmax
(
y: Tensor,
name: str | None = None
)
Tensor
fmax¶
-
Compares the elements at the corresponding positions of the two tensors and returns a new tensor containing the maximum value of the element. If one of them is a nan value, the other value is directly returned, if both are nan values, then the first nan value is returned. The equation is:
\[out = fmax(x, y)\]Note
paddle.fmaxsupports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .- Parameters
-
x (Tensor) – the input tensor, it’s data type should be bfloat16, float16, float32, float64, int32, int64.
y (Tensor) – the input tensor, it’s data type should be bfloat16, float16, float32, float64, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
N-D Tensor. A location into which the result is stored. If x, y have different shapes and are “broadcastable”, the resulting tensor shape is the shape of x and y after broadcasting. If x, y have the same shape, its shape is the same as x and y.
Examples
>>> import paddle >>> x = paddle.to_tensor([[1, 2], [7, 8]]) >>> y = paddle.to_tensor([[3, 4], [5, 6]]) >>> res = paddle.fmax(x, y) >>> print(res) Tensor(shape=[2, 2], dtype=int64, place=Place(cpu), stop_gradient=True, [[3, 4], [7, 8]]) >>> x = paddle.to_tensor([[1, 2, 3], [1, 2, 3]]) >>> y = paddle.to_tensor([3, 0, 4]) >>> res = paddle.fmax(x, y) >>> print(res) Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[3, 2, 4], [3, 2, 4]]) >>> x = paddle.to_tensor([2, 3, 5], dtype='float32') >>> y = paddle.to_tensor([1, float("nan"), float("nan")], dtype='float32') >>> res = paddle.fmax(x, y) >>> print(res) Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True, [2., 3., 5.]) >>> x = paddle.to_tensor([5, 3, float("inf")], dtype='float32') >>> y = paddle.to_tensor([1, -float("inf"), 5], dtype='float32') >>> res = paddle.fmax(x, y) >>> print(res) Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True, [5. , 3. , inf.])
-
fmin
(
y: Tensor,
name: str | None = None
)
Tensor
fmin¶
-
Compares the elements at the corresponding positions of the two tensors and returns a new tensor containing the minimum value of the element. If one of them is a nan value, the other value is directly returned, if both are nan values, then the first nan value is returned. The equation is:
\[out = fmin(x, y)\]Note
paddle.fminsupports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .- Parameters
-
x (Tensor) – the input tensor, it’s data type should be bfloat16, float16, float32, float64, int32, int64.
y (Tensor) – the input tensor, it’s data type should be bfloat16, float16, float32, float64, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
N-D Tensor. A location into which the result is stored. If x, y have different shapes and are “broadcastable”, the resulting tensor shape is the shape of x and y after broadcasting. If x, y have the same shape, its shape is the same as x and y.
Examples
>>> import paddle >>> x = paddle.to_tensor([[1, 2], [7, 8]]) >>> y = paddle.to_tensor([[3, 4], [5, 6]]) >>> res = paddle.fmin(x, y) >>> print(res) Tensor(shape=[2, 2], dtype=int64, place=Place(cpu), stop_gradient=True, [[1, 2], [5, 6]]) >>> x = paddle.to_tensor([[[1, 2, 3], [1, 2, 3]]]) >>> y = paddle.to_tensor([3, 0, 4]) >>> res = paddle.fmin(x, y) >>> print(res) Tensor(shape=[1, 2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[[1, 0, 3], [1, 0, 3]]]) >>> x = paddle.to_tensor([2, 3, 5], dtype='float32') >>> y = paddle.to_tensor([1, float("nan"), float("nan")], dtype='float32') >>> res = paddle.fmin(x, y) >>> print(res) Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True, [1., 3., 5.]) >>> x = paddle.to_tensor([5, 3, float("inf")], dtype='float64') >>> y = paddle.to_tensor([1, -float("inf"), 5], dtype='float64') >>> res = paddle.fmin(x, y) >>> print(res) Tensor(shape=[3], dtype=float64, place=Place(cpu), stop_gradient=True, [ 1. , -inf., 5. ])
-
frac
(
name: str | None = None
)
Tensor
frac¶
-
This API is used to return the fractional portion of each element in input.
- Parameters
-
x (Tensor) – The input tensor, which data type should be int32, int64, float32, float64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
The output Tensor of frac.
- Return type
-
Tensor
Examples
>>> import paddle >>> input = paddle.to_tensor([[12.22000003, -1.02999997], ... [-0.54999995, 0.66000003]]) >>> output = paddle.frac(input) >>> output Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True, [[ 0.22000003, -0.02999997], [-0.54999995, 0.66000003]])
-
frac_
(
name: str | None = None
)
Tensor
frac_¶
-
Inplace version of
fracAPI, the output Tensor will be inplaced with inputx. Please refer to frac.
-
frexp
(
name: str | None = None
)
tuple[Tensor, Tensor]
frexp¶
-
The function used to decompose a floating point number into mantissa and exponent.
- Parameters
-
x (Tensor) – The input tensor, it’s data type should be float32, float64.
name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Returns
-
-
- mantissa (Tensor), A mantissa Tensor. The shape and data type of mantissa tensor and exponential tensor are
-
the same as those of input.
-
- exponent (Tensor), A exponent Tensor. The shape and data type of mantissa tensor and exponential tensor are
-
the same as those of input.
-
Examples
>>> import paddle >>> x = paddle.to_tensor([[1, 2, 3, 4]], dtype="float32") >>> mantissa, exponent = paddle.tensor.math.frexp(x) >>> mantissa Tensor(shape=[1, 4], dtype=float32, place=Place(cpu), stop_gradient=True, [[0.50000000, 0.50000000, 0.75000000, 0.50000000]]) >>> exponent Tensor(shape=[1, 4], dtype=float32, place=Place(cpu), stop_gradient=True, [[1., 2., 2., 3.]])
-
gammainc
(
y: Tensor,
name: str | None = None
)
Tensor
gammainc¶
-
Computes the regularized lower incomplete gamma function.
\[P(x, y) = \frac{1}{\Gamma(x)} \int_{0}^{y} t^{x-1} e^{-t} dt\]- Parameters
-
x (Tensor) – The non-negative argument Tensor. Must be one of the following types: float32, float64.
y (Tensor) – The positive parameter Tensor. Must be one of the following types: float32, float64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, the gammainc of the input Tensor.
Examples
>>> import paddle >>> x = paddle.to_tensor([0.5, 0.5, 0.5, 0.5, 0.5], dtype="float32") >>> y = paddle.to_tensor([0, 1, 10, 100, 1000], dtype="float32") >>> out = paddle.gammainc(x, y) >>> print(out) Tensor(shape=[5], dtype=float32, place=Place(cpu), stop_gradient=True, [0. , 0.84270084, 0.99999225, 1. , 1. ])
-
gammainc_
(
y: Tensor,
name: str | None = None
)
Tensor
gammainc_¶
-
Inplace version of
gammaincAPI, the output Tensor will be inplaced with inputx. Please refer to gammainc.
-
gammaincc
(
y: Tensor,
name: str | None = None
)
Tensor
gammaincc¶
-
Computes the regularized upper incomplete gamma function.
\[Q(x, y) = \frac{1}{\Gamma(x)} \int_{y}^{\infty} t^{x-1} e^{-t} dt\]- Parameters
-
x (Tensor) – The non-negative argument Tensor. Must be one of the following types: float32, float64.
y (Tensor) – The positive parameter Tensor. Must be one of the following types: float32, float64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, the gammaincc of the input Tensor.
Examples
>>> import paddle >>> x = paddle.to_tensor([0.5, 0.5, 0.5, 0.5, 0.5], dtype="float32") >>> y = paddle.to_tensor([0, 1, 10, 100, 1000], dtype="float32") >>> out = paddle.gammaincc(x, y) >>> print(out) Tensor(shape=[5], dtype=float32, place=Place(cpu), stop_gradient=True, [1. , 0.15729916, 0.00000774, 0. , 0. ])
-
gammaincc_
(
y: Tensor,
name: str | None = None
)
Tensor
gammaincc_¶
-
Inplace version of
gammainccAPI, the output Tensor will be inplaced with inputx. Please refer to gammaincc.
-
gammaln
(
name: str | None = None
)
Tensor
gammaln¶
-
Calculates the logarithm of the absolute value of the gamma function elementwisely.
- Parameters
-
x (Tensor) – Input Tensor. Must be one of the following types: float16, float32, float64, bfloat16.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, The values of the logarithm of the absolute value of the gamma at the given tensor x.
Examples
>>> import paddle >>> x = paddle.arange(1.5, 4.5, 0.5) >>> out = paddle.gammaln(x) >>> print(out) Tensor(shape=[6], dtype=float32, place=Place(cpu), stop_gradient=True, [-0.12078224, 0. , 0.28468287, 0.69314718, 1.20097363, 1.79175949])
-
gammaln_
(
name: str | None = None
)
Tensor
gammaln_¶
-
Inplace version of
gammalnAPI, the output Tensor will be inplaced with inputx. Please refer to gammaln.
-
gather
(
index: Tensor,
axis: Tensor | int | None = None,
name: str | None = None
)
Tensor
gather¶
-
Output is obtained by gathering entries of
axisofxindexed byindexand concatenate them together.Given: x = [[1, 2], [3, 4], [5, 6]] index = [1, 2] axis=[0] Then: out = [[3, 4], [5, 6]]- Parameters
-
x (Tensor) – The source input tensor with rank>=1. Supported data type is int32, int64, float32, float64, complex64, complex128 and uint8 (only for CPU), float16 (only for GPU).
index (Tensor) – The index input tensor with rank=0 or rank=1. Data type is int32 or int64.
axis (Tensor|int|None, optional) – The axis of input to be gathered, it’s can be int or a Tensor with data type is int32 or int64. The default value is None, if None, the
axisis 0.name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name .
- Returns
-
output (Tensor), If the index is a 1-D tensor, the output is a tensor with the same shape as
x. If the index is a 0-D tensor, the output will reduce the dimension where the axis pointing.
Examples
>>> import paddle >>> input = paddle.to_tensor([[1,2],[3,4],[5,6]]) >>> index = paddle.to_tensor([0,1]) >>> output = paddle.gather(input, index, axis=0) >>> print(output) Tensor(shape=[2, 2], dtype=int64, place=Place(cpu), stop_gradient=True, [[1, 2], [3, 4]])
-
gather_nd
(
index: Tensor,
name: str | None = None
)
Tensor
gather_nd¶
-
This function is actually a high-dimensional extension of
gatherand supports for simultaneous indexing by multiple axes.indexis a K-dimensional integer tensor, which is regarded as a (K-1)-dimensional tensor ofindexintoinput, where each element defines a slice of params:\[output[(i_0, ..., i_{K-2})] = input[index[(i_0, ..., i_{K-2})]]\]Obviously,
index.shape[-1] <= input.rank. And, the output tensor has shapeindex.shape[:-1] + input.shape[index.shape[-1]:].Given: x = [[[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11]], [[12, 13, 14, 15], [16, 17, 18, 19], [20, 21, 22, 23]]] x.shape = (2, 3, 4) * Case 1: index = [[1]] gather_nd(x, index) = [x[1, :, :]] = [[12, 13, 14, 15], [16, 17, 18, 19], [20, 21, 22, 23]] * Case 2: index = [[0,2]] gather_nd(x, index) = [x[0, 2, :]] = [8, 9, 10, 11] * Case 3: index = [[1, 2, 3]] gather_nd(x, index) = [x[1, 2, 3]] = [23]- Parameters
-
x (Tensor) – The input Tensor which it’s data type should be bool, float16, float32, float64, int32, int64.
index (Tensor) – The index input with rank > 1, index.shape[-1] <= input.rank. Its dtype should be int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
-1] + input.shape[index.shape[-1]:]
- Return type
-
output (Tensor), A tensor with the shape index.shape[
Examples
>>> import paddle >>> x = paddle.to_tensor([[[1, 2], [3, 4], [5, 6]], ... [[7, 8], [9, 10], [11, 12]]]) >>> index = paddle.to_tensor([[0, 1]]) >>> output = paddle.gather_nd(x, index) >>> print(output) Tensor(shape=[1, 2], dtype=int64, place=Place(cpu), stop_gradient=True, [[3, 4]])
-
gcd
(
y: Tensor,
name: str | None = None
)
Tensor
gcd¶
-
Computes the element-wise greatest common divisor (GCD) of input |x| and |y|. Both x and y must have integer types.
Note
gcd(0,0)=0, gcd(0, y)=|y|
If x.shape != y.shape, they must be broadcastable to a common shape (which becomes the shape of the output).
- Parameters
-
x (Tensor) – An N-D Tensor, the data type is int32, int64.
y (Tensor) – An N-D Tensor, the data type is int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
An N-D Tensor, the data type is the same with input.
- Return type
-
out (Tensor)
Examples
>>> import paddle >>> x1 = paddle.to_tensor(12) >>> x2 = paddle.to_tensor(20) >>> paddle.gcd(x1, x2) Tensor(shape=[], dtype=int64, place=Place(cpu), stop_gradient=True, 4) >>> x3 = paddle.arange(6) >>> paddle.gcd(x3, x2) Tensor(shape=[6], dtype=int64, place=Place(cpu), stop_gradient=True, [20, 1 , 2 , 1 , 4 , 5]) >>> x4 = paddle.to_tensor(0) >>> paddle.gcd(x4, x2) Tensor(shape=[], dtype=int64, place=Place(cpu), stop_gradient=True, 20) >>> paddle.gcd(x4, x4) Tensor(shape=[], dtype=int64, place=Place(cpu), stop_gradient=True, 0) >>> x5 = paddle.to_tensor(-20) >>> paddle.gcd(x1, x5) Tensor(shape=[], dtype=int64, place=Place(cpu), stop_gradient=True, 4)
-
gcd_
(
y: Tensor,
name: str | None = None
)
Tensor
gcd_¶
-
Inplace version of
gcdAPI, the output Tensor will be inplaced with inputx. Please refer to gcd.
-
geometric_
(
probs: float | paddle.Tensor,
name: str | None = None
)
Tensor
geometric_¶
-
Fills the tensor with numbers drawn from the Geometric distribution.
- Parameters
-
x (Tensor) – the tensor will be filled, The data type is float32 or float64.
probs (float|Tensor) – Probability parameter. The value of probs must be positive. When the parameter is a tensor, probs is probability of success for each trial.
name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Returns
-
input tensor with numbers drawn from the Geometric distribution.
- Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.randn([3, 4]) >>> x.geometric_(0.3) >>> >>> print(x) Tensor(shape=[3, 4], dtype=float32, place=Place(cpu), stop_gradient=True, [[2.42739224, 4.78268528, 1.23302543, 3.76555204], [1.38877118, 0.16075331, 0.16401523, 2.47349310], [1.72872102, 2.76533413, 0.33410925, 1.63351011]])
-
greater_equal
(
y: Tensor,
name: str | None = None
)
Tensor
greater_equal¶
-
Returns the truth value of \(x >= y\) elementwise, which is equivalent function to the overloaded operator >=.
Note
The output has no gradient.
- Parameters
-
x (Tensor) – First input to compare which is N-D tensor. The input data type should be bool, bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64, complex64, complex128.
y (Tensor) – Second input to compare which is N-D tensor. The input data type should be bool, bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64, complex64, complex128.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
- Returns
-
The output shape is same as input
x. The output data type is bool. - Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.to_tensor([1, 2, 3]) >>> y = paddle.to_tensor([1, 3, 2]) >>> result1 = paddle.greater_equal(x, y) >>> print(result1) Tensor(shape=[3], dtype=bool, place=Place(cpu), stop_gradient=True, [True , False, True ])
-
greater_equal_
(
y: Tensor,
name: str | None = None
)
Tensor
greater_equal_¶
-
Inplace version of
greater_equalAPI, the output Tensor will be inplaced with inputx. Please refer to greater_equal.
-
greater_than
(
)
greater_than¶
-
C++ interface function for greater_than.
-
greater_than_
(
y: Tensor,
name: str | None = None
)
Tensor
greater_than_¶
-
Inplace version of
greater_thanAPI, the output Tensor will be inplaced with inputx. Please refer to greater_than.
-
heaviside
(
y: Tensor,
name: str | None = None
)
Tensor
heaviside¶
-
Computes the Heaviside step function determined by corresponding element in y for each element in x. The equation is
\[\begin{split}heaviside(x, y)= \left\{ \begin{array}{lcl} 0,& &\text{if} \ x < 0, \\ y,& &\text{if} \ x = 0, \\ 1,& &\text{if} \ x > 0. \end{array} \right.\end{split}\]Note
paddle.heavisidesupports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .- Parameters
-
x (Tensor) – The input tensor of Heaviside step function, it’s data type should be bfloat16, float16, float32, float64, int32 or int64.
y (Tensor) – The tensor that determines a Heaviside step function, it’s data type should be bfloat16, float16, float32, float64, int32 or int64.
name (str|None, optional) – Name for the operation (optional, default is None). Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
- Returns
-
N-D Tensor. A location into which the result is stored. If x and y have different shapes and are broadcastable, the resulting tensor shape is the shape of x and y after broadcasting. If x, y have the same shape, its shape is the same as x and y.
Examples
>>> import paddle >>> x = paddle.to_tensor([-0.5, 0, 0.5]) >>> y = paddle.to_tensor([0.1]) >>> paddle.heaviside(x, y) Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True, [0. , 0.10000000, 1. ]) >>> x = paddle.to_tensor([[-0.5, 0, 0.5], [-0.5, 0.5, 0]]) >>> y = paddle.to_tensor([0.1, 0.2, 0.3]) >>> paddle.heaviside(x, y) Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True, [[0. , 0.20000000, 1. ], [0. , 1. , 0.30000001]])
-
histogram
(
bins: int = 100,
min: float = 0.0,
max: float = 0.0,
weight: Tensor | None = None,
density: bool = False,
name: str | None = None
)
Tensor
histogram¶
-
Computes the histogram of a tensor. The elements are sorted into equal width bins between min and max. If min and max are both zero, the minimum and maximum values of the data are used.
- Parameters
-
input (Tensor) – A Tensor with shape \([N_1, N_2,..., N_k]\) . The data type of the input Tensor should be float32, float64, int32, int64.
bins (int, optional) – number of histogram bins. Default: 100.
min (float, optional) – lower end of the range (inclusive). Default: 0.0.
max (float, optional) – upper end of the range (inclusive). Default: 0.0.
weight (Tensor, optional) – If provided, it must have the same shape as input. Each value in input contributes its associated weight towards the bin count (instead of 1). Default: None.
density (bool, optional) – If False, the result will contain the count (or total weight) in each bin. If True, the result is the value of the probability density function over the bins, normalized such that the integral over the range of the bins is 1.
name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Returns
-
Tensor, shape is (nbins,), the counts or density of the histogram.
Examples
>>> import paddle >>> inputs = paddle.to_tensor([1, 2, 1]) >>> result = paddle.histogram(inputs, bins=4, min=0, max=3) >>> print(result) Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True, [0, 2, 1, 0])
-
histogram_bin_edges
(
bins: int = 100,
min: float = 0.0,
max: float = 0.0,
name: str | None = None
)
Tensor
histogram_bin_edges¶
-
Computes only the edges of the bins used by the histogram function. If min and max are both zero, the minimum and maximum values of the data are used.
- Parameters
-
input (Tensor) – The data type of the input Tensor should be float32, float64, int32, int64.
bins (int, optional) – number of histogram bins.
min (float, optional) – lower end of the range (inclusive). Default: 0.0.
max (float, optional) – upper end of the range (inclusive). Default: 0.0.
name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Returns
-
Tensor, the values of the bin edges. The output data type will be float32.
Examples
>>> import paddle >>> inputs = paddle.to_tensor([1, 2, 1]) >>> result = paddle.histogram_bin_edges(inputs, bins=4, min=0, max=3) >>> print(result) Tensor(shape=[5], dtype=float32, place=Place(cpu), stop_gradient=True, [0. , 0.75000000, 1.50000000, 2.25000000, 3. ])
-
histogramdd
(
bins: Tensor | list[int] | int = 10,
ranges: Sequence[float] | None = None,
density: bool = False,
weights: Tensor | None = None,
name: str | None = None
)
tuple[Tensor, list[Tensor]]
histogramdd¶
-
Computes a multi-dimensional histogram of the values in a tensor.
Interprets the elements of an input tensor whose innermost dimension has size N as a collection of N-dimensional points. Maps each of the points into a set of N-dimensional bins and returns the number of points (or total weight) in each bin.
input x must be a tensor with at least 2 dimensions. If input has shape (M, N), each of its M rows defines a point in N-dimensional space. If input has three or more dimensions, all but the last dimension are flattened.
Each dimension is independently associated with its own strictly increasing sequence of bin edges. Bin edges may be specified explicitly by passing a sequence of 1D tensors. Alternatively, bin edges may be constructed automatically by passing a sequence of integers specifying the number of equal-width bins in each dimension.
- Parameters
-
x (Tensor) – The input tensor.
bins (list[Tensor], list[int], or int) – If list[Tensor], defines the sequences of bin edges. If list[int], defines the number of equal-width bins in each dimension. If int, defines the number of equal-width bins for all dimensions.
ranges (sequence[float]|None, optional) – Defines the leftmost and rightmost bin edges in each dimension. If is None, set the minimum and maximum as leftmost and rightmost edges for each dimension.
density (bool, optional) – If False (default), the result will contain the count (or total weight) in each bin. If True, each count (weight) is divided by the total count (total weight), then divided by the volume of its associated bin.
weights (Tensor, optional) – By default, each value in the input has weight 1. If a weight tensor is passed, each N-dimensional coordinate in input contributes its associated weight towards its bin’s result. The weight tensor should have the same shape as the input tensor excluding its innermost dimension N.
name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Returns
-
N-dimensional Tensor containing the values of the histogram.
bin_edges(Tensor[]), sequence of N 1D Tensors containing the bin edges.
Examples
>>> import paddle >>> x = paddle.to_tensor([[0., 1.], [1., 0.], [2.,0.], [2., 2.]]) >>> bins = [3,3] >>> weights = paddle.to_tensor([1., 2., 4., 8.]) >>> paddle.histogramdd(x, bins=bins, weights=weights) (Tensor(shape=[3, 3], dtype=float32, place=Place(gpu:0), stop_gradient=True, [[0., 1., 0.], [2., 0., 0.], [4., 0., 8.]]), [Tensor(shape=[4], dtype=float32, place=Place(gpu:0), stop_gradient=True, [0. , 0.66666669, 1.33333337, 2. ]), Tensor(shape=[4], dtype=float32, place=Place(gpu:0), stop_gradient=True, [0. , 0.66666669, 1.33333337, 2. ])])
>>> import paddle >>> y = paddle.to_tensor([[0., 0.], [1., 1.], [2., 2.]]) >>> bins = [2,2] >>> ranges = [0., 1., 0., 1.] >>> density = True >>> paddle.histogramdd(y, bins=bins, ranges=ranges, density=density) (Tensor(shape=[2, 2], dtype=float32, place=Place(gpu:0), stop_gradient=True, [[2., 0.], [0., 2.]]), [Tensor(shape=[3], dtype=float32, place=Place(gpu:0), stop_gradient=True, [0. , 0.50000000, 1. ]), Tensor(shape=[3], dtype=float32, place=Place(gpu:0), stop_gradient=True, [0. , 0.50000000, 1. ])])
-
householder_product
(
tau: Tensor,
name: str | None = None
)
Tensor
householder_product¶
-
Computes the first n columns of a product of Householder matrices.
This function can get the vector \(\omega_{i}\) from matrix x (m x n), the \(i-1\) elements are zeros, and the i-th is 1, the rest of the elements are from i-th column of x. And with the vector tau can calculate the first n columns of a product of Householder matrices.
\(H_i = I_m - \tau_i \omega_i \omega_i^H\)
- Parameters
- Returns
-
Tensor, the dtype is same as input tensor, the Q in QR decomposition.
\(out = Q = H_1H_2H_3...H_k\)
Examples
>>> import paddle >>> x = paddle.to_tensor([[-1.1280, 0.9012, -0.0190], ... [ 0.3699, 2.2133, -1.4792], ... [ 0.0308, 0.3361, -3.1761], ... [-0.0726, 0.8245, -0.3812]]) >>> tau = paddle.to_tensor([1.7497, 1.1156, 1.7462]) >>> Q = paddle.linalg.householder_product(x, tau) >>> print(Q) Tensor(shape=[4, 3], dtype=float32, place=Place(gpu:0), stop_gradient=True, [[-0.74969995, -0.02181768, 0.31115776], [-0.64721400, -0.12367040, -0.21738708], [-0.05389076, -0.37562513, -0.84836429], [ 0.12702821, -0.91822827, 0.36892807]])
-
hsplit
(
num_or_indices: int | Sequence[int],
name: str | None = None
)
list[Tensor]
hsplit¶
-
hsplitFull name Horizontal Split, splits the input Tensor into multiple sub-Tensors along the horizontal axis, in the following two cases:When the dimension of x is equal to 1, it is equivalent to
paddle.tensor_splitwithaxis=0;
when the dimension of x is greater than 1, it is equivalent to
paddle.tensor_splitwithaxis=1.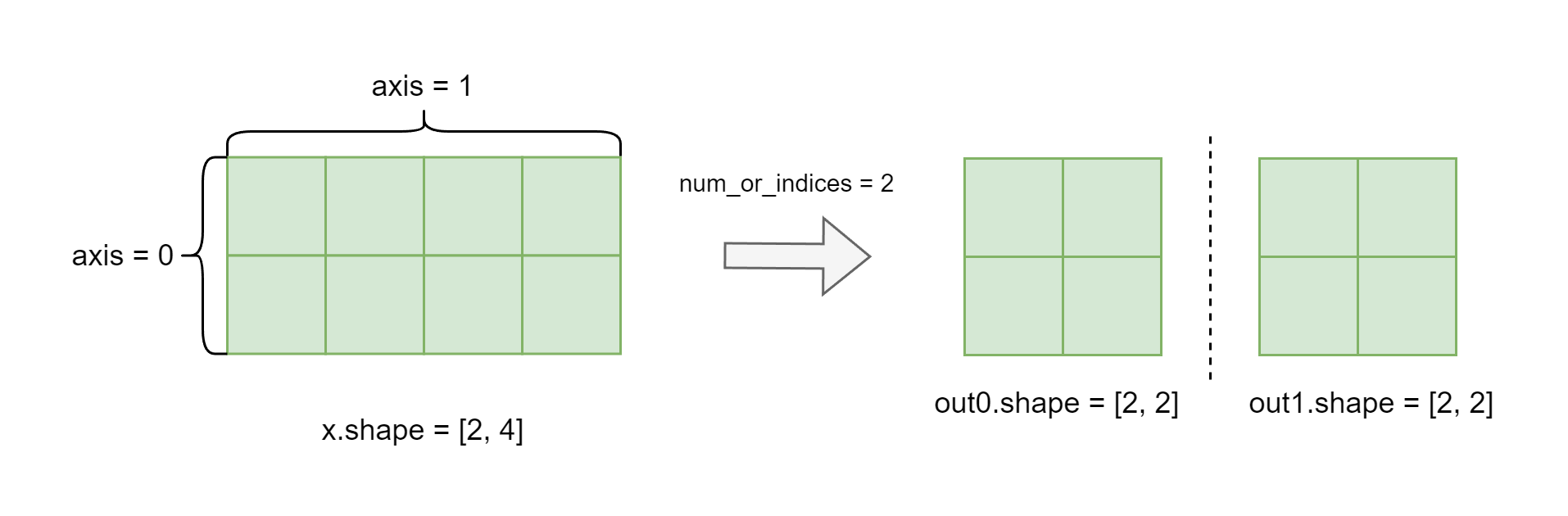
- Parameters
-
x (Tensor) – A Tensor whose dimension must be greater than 0. The data type is bool, bfloat16, float16, float32, float64, uint8, int32 or int64.
num_or_indices (int|list|tuple) – If
num_or_indicesis an intn,xis split intonsections. Ifnum_or_indicesis a list or tuple of integer indices,xis split at each of the indices.name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name .
- Returns
-
list[Tensor], The list of segmented Tensors.
Examples
>>> import paddle >>> # x is a Tensor of shape [8] >>> x = paddle.rand([8]) >>> out0, out1 = paddle.hsplit(x, num_or_indices=2) >>> print(out0.shape) [4] >>> print(out1.shape) [4] >>> # x is a Tensor of shape [7, 8] >>> x = paddle.rand([7, 8]) >>> out0, out1 = paddle.hsplit(x, num_or_indices=2) >>> print(out0.shape) [7, 4] >>> print(out1.shape) [7, 4] >>> out0, out1, out2 = paddle.hsplit(x, num_or_indices=[1, 4]) >>> print(out0.shape) [7, 1] >>> print(out1.shape) [7, 3] >>> print(out2.shape) [7, 4]
-
hypot
(
y: Tensor,
name: str | None = None
)
Tensor
hypot¶
-
Calculate the length of the hypotenuse of a right-angle triangle. The equation is:
\[out = {\sqrt{x^2 + y^2}}\]- Parameters
-
x (Tensor) – The input Tensor, the data type is float32, float64, int32 or int64.
y (Tensor) – The input Tensor, the data type is float32, float64, int32 or int64.
name (str|None, optional) – Name for the operation (optional, default is None).For more information, please refer to api_guide_Name.
- Returns
-
An N-D Tensor. If x, y have different shapes and are “broadcastable”, the resulting tensor shape is the shape of x and y after broadcasting. If x, y have the same shape, its shape is the same as x and y. And the data type is float32 or float64.
- Return type
-
out (Tensor)
Examples
>>> import paddle >>> x = paddle.to_tensor([3], dtype='float32') >>> y = paddle.to_tensor([4], dtype='float32') >>> res = paddle.hypot(x, y) >>> print(res) Tensor(shape=[1], dtype=float32, place=Place(cpu), stop_gradient=True, [5.])
-
hypot_
(
y: Tensor,
name: str | None = None
)
Tensor
hypot_¶
-
Inplace version of
hypotAPI, the output Tensor will be inplaced with inputx. Please refer to hypot.
-
i0
(
name: str | None = None
)
Tensor
i0¶
-
The function used to calculate modified bessel function of order 0.
- Equation:
-
\[I_0(x) = \sum^{\infty}_{k=0}\frac{(x^2/4)^k}{(k!)^2}\]
- Parameters
-
x (Tensor) – The input tensor, it’s data type should be float32, float64, uint8, int8, int16, int32, int64.
name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Returns
-
-
- out (Tensor), A Tensor. the value of the modified bessel function of order 0 at x
-
(integer types are autocasted into float32).
-
Examples
>>> import paddle >>> x = paddle.to_tensor([0, 1, 2, 3, 4], dtype="float32") >>> paddle.i0(x) Tensor(shape=[5], dtype=float32, place=Place(cpu), stop_gradient=True, [0.99999994 , 1.26606596 , 2.27958512 , 4.88079262 , 11.30192089])
-
i0_
(
name: str | None = None
)
Tensor
i0_¶
-
Inplace version of
i0API, the output Tensor will be inplaced with inputx. Please refer to i0.
-
i0e
(
name: str | None = None
)
Tensor
i0e¶
-
The function used to calculate exponentially scaled modified Bessel function of order 0.
- Equation:
-
\[\begin{split}I_0(x) = \sum^{\infty}_{k=0}\frac{(x^2/4)^k}{(k!)^2} \\ I_{0e}(x) = e^{-|x|}I_0(x)\end{split}\]
- Parameters
-
x (Tensor) – The input tensor, it’s data type should be float32, float64, uint8, int8, int16, int32, int64.
name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Returns
-
-
- out (Tensor), A Tensor. the value of the exponentially scaled modified Bessel function of order 0 at x
-
(integer types are autocasted into float32).
-
Examples
>>> import paddle >>> x = paddle.to_tensor([0, 1, 2, 3, 4], dtype="float32") >>> print(paddle.i0e(x)) Tensor(shape=[5], dtype=float32, place=Place(cpu), stop_gradient=True, [0.99999994, 0.46575963, 0.30850831, 0.24300036, 0.20700191])
-
i1
(
name: str | None = None
)
Tensor
i1¶
-
The function is used to calculate modified bessel function of order 1.
- Parameters
-
x (Tensor) – The input tensor, it’s data type should be float32, float64, uint8, int8, int16, int32, int64.
name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Returns
-
-
- out (Tensor), A Tensor. the value of the modified bessel function of order 1 at x
-
(integer types are autocasted into float32).
-
Examples
>>> import paddle >>> x = paddle.to_tensor([0, 1, 2, 3, 4], dtype="float32") >>> print(paddle.i1(x)) Tensor(shape=[5], dtype=float32, place=Place(cpu), stop_gradient=True, [0. , 0.56515908, 1.59063685, 3.95337057, 9.75946712])
-
i1e
(
name: str | None = None
)
Tensor
i1e¶
-
The function is used to calculate exponentially scaled modified Bessel function of order 1.
- Parameters
-
x (Tensor) – The input tensor, it’s data type should be float32, float64, uint8, int8, int16, int32, int64.
name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Returns
-
-
- out (Tensor), A Tensor. the value of the exponentially scaled modified Bessel function of order 1 at x
-
(integer types are autocasted into float32).
-
Examples
>>> import paddle >>> x = paddle.to_tensor([0, 1, 2, 3, 4], dtype="float32") >>> print(paddle.i1e(x)) Tensor(shape=[5], dtype=float32, place=Place(cpu), stop_gradient=True, [0. , 0.20791042, 0.21526928, 0.19682673, 0.17875087])
-
imag
(
name: str | None = None
)
Tensor
imag¶
-
Returns a new tensor containing imaginary values of input tensor.
- Parameters
-
x (Tensor) – the input tensor, its data type could be complex64 or complex128.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name .
- Returns
-
a tensor containing imaginary values of the input tensor.
- Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.to_tensor( ... [[1 + 6j, 2 + 5j, 3 + 4j], [4 + 3j, 5 + 2j, 6 + 1j]]) >>> print(x) Tensor(shape=[2, 3], dtype=complex64, place=Place(cpu), stop_gradient=True, [[(1+6j), (2+5j), (3+4j)], [(4+3j), (5+2j), (6+1j)]]) >>> imag_res = paddle.imag(x) >>> print(imag_res) Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True, [[6., 5., 4.], [3., 2., 1.]]) >>> imag_t = x.imag() >>> print(imag_t) Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True, [[6., 5., 4.], [3., 2., 1.]])
-
increment
(
value: float = 1.0,
name: str | None = None
)
Tensor
increment¶
-
The API is usually used for control flow to increment the data of
xby an amountvalue. Notice that the number of elements inxmust be equal to 1.- Parameters
-
x (Tensor) – A tensor that must always contain only one element, its data type supports float32, float64, int32 and int64.
value (float, optional) – The amount to increment the data of
x. Default: 1.0.name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, the elementwise-incremented tensor with the same shape and data type as
x.
Examples
>>> import paddle >>> data = paddle.zeros(shape=[1], dtype='float32') >>> counter = paddle.increment(data) >>> counter Tensor(shape=[1], dtype=float32, place=Place(cpu), stop_gradient=True, [1.])
-
index_add
(
index: Tensor,
axis: int,
value: Tensor,
name: str | None = None
)
Tensor
index_add¶
-
Adds the elements of the input tensor with value tensor by selecting the indices in the order given in index.
- Parameters
-
x (Tensor) – The Destination Tensor. Supported data types are int32, int64, float16, float32, float64.
index (Tensor) – The 1-D Tensor containing the indices to index. The data type of
indexmust be int32 or int64.axis (int) – The dimension in which we index.
value (Tensor) – The tensor used to add the elements along the target axis.
name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Returns
-
Tensor, same dimension and dtype with x.
Examples
>>> >>> import paddle >>> paddle.device.set_device('gpu') >>> input_tensor = paddle.to_tensor(paddle.ones((3, 3)), dtype="float32") >>> index = paddle.to_tensor([0, 2], dtype="int32") >>> value = paddle.to_tensor([[1, 1, 1], [1, 1, 1]], dtype="float32") >>> outplace_res = paddle.index_add(input_tensor, index, 0, value) >>> print(outplace_res) Tensor(shape=[3, 3], dtype=float32, place=Place(gpu:0), stop_gradient=True, [[2., 2., 2.], [1., 1., 1.], [2., 2., 2.]])
-
index_add_
(
index: Tensor,
axis: int,
value: Tensor,
name: str | None = None
)
Tensor
index_add_¶
-
Inplace version of
index_addAPI, the output Tensor will be inplaced with inputx. Please refer to index_add.
-
index_fill
(
index: Tensor,
axis: int,
value: float,
name: str | None = None
)
index_fill¶
-
Fill the elements of the input tensor with value by the specific axis and index.
As shown below, a
[3, 3]2D tensor is updated via the index_fill operation. Withaxis=0,index=[0, 2]andvalue=-1, the 1st and 3rd row elements become-1. The resulting tensor, still [3, 3], has updated values.
- Parameters
-
x (Tensor) – The Destination Tensor. Supported data types are int32, int64, float16, float32, float64.
index (Tensor) – The 1-D Tensor containing the indices to index. The data type of
indexmust be int32 or int64.axis (int) – The dimension along which to index.
value (int|float) – The tensor used to fill with.
name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Returns
-
Tensor, same dimension and dtype with x.
Examples
>>> import paddle >>> input_tensor = paddle.to_tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9]], dtype='int64') >>> index = paddle.to_tensor([0, 2], dtype="int32") >>> value = -1 >>> res = paddle.index_fill(input_tensor, index, 0, value) >>> print(input_tensor) Tensor(shape=[3, 3], dtype=int64, place=Place(gpu:0), stop_gradient=True, [[1, 2, 3], [4, 5, 6], [7, 8, 9]]) >>> print(res) Tensor(shape=[3, 3], dtype=int64, place=Place(gpu:0), stop_gradient=True, [[-1, -1, -1], [ 4, 5, 6], [-1, -1, -1]])
-
index_fill_
(
index: Tensor,
axis: int,
value: float,
name: str | None = None
)
index_fill_¶
-
Inplace version of
index_fillAPI, the output Tensor will be inplaced with inputx. Please refer to index_fill.
-
index_put
(
indices: Sequence[Tensor],
value: Tensor,
accumulate: bool = False,
name: str | None = None
)
Tensor
index_put¶
-
Puts values from the tensor values into the tensor x using the indices specified in indices (which is a tuple of Tensors). The expression paddle.index_put_(x, indices, values) is equivalent to tensor[indices] = values. Returns x. If accumulate is True, the elements in values are added to x. If accumulate is False, the behavior is undefined if indices contain duplicate elements.
- Parameters
-
x (Tensor) – The Source Tensor. Supported data types are int32, int64, float16, float32, float64, bool.
indices (list[Tensor]|tuple[Tensor]) – The tuple of Tensor containing the indices to index. The data type of
tensor in indicesmust be int32, int64 or bool.value (Tensor) – The tensor used to be assigned to x.
accumulate (bool, optional) – Whether the elements in values are added to x. Default: False.
name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Returns
-
Tensor, same dimension and dtype with x.
Examples
>>> import paddle >>> x = paddle.zeros([3, 3]) >>> value = paddle.ones([3]) >>> ix1 = paddle.to_tensor([0,1,2]) >>> ix2 = paddle.to_tensor([1,2,1]) >>> indices=(ix1,ix2) >>> out = paddle.index_put(x,indices,value) >>> print(x) Tensor(shape=[3, 3], dtype=float32, place=Place(cpu), stop_gradient=True, [[0., 0., 0.], [0., 0., 0.], [0., 0., 0.]]) >>> print(out) Tensor(shape=[3, 3], dtype=float32, place=Place(cpu), stop_gradient=True, [[0., 1., 0.], [0., 0., 1.], [0., 1., 0.]])
-
index_put_
(
indices: Sequence[Tensor],
value: Tensor,
accumulate: bool = False,
name: str | None = None
)
Tensor
index_put_¶
-
Inplace version of
index_putAPI, the output Tensor will be inplaced with inputx. Please refer to index_put.
-
index_sample
(
index: Tensor
)
Tensor
index_sample¶
-
IndexSample Layer
IndexSample OP returns the element of the specified location of X, and the location is specified by Index.
Given: X = [[1, 2, 3, 4, 5], [6, 7, 8, 9, 10]] Index = [[0, 1, 3], [0, 2, 4]] Then: Out = [[1, 2, 4], [6, 8, 10]]- Parameters
-
x (Tensor) – The source input tensor with 2-D shape. Supported data type is int32, int64, bfloat16, float16, float32, float64, complex64, complex128.
index (Tensor) – The index input tensor with 2-D shape, first dimension should be same with X. Data type is int32 or int64.
- Returns
-
Tensor, The output is a tensor with the same shape as index.
Examples
>>> import paddle >>> x = paddle.to_tensor([[1.0, 2.0, 3.0, 4.0], ... [5.0, 6.0, 7.0, 8.0], ... [9.0, 10.0, 11.0, 12.0]], dtype='float32') >>> index = paddle.to_tensor([[0, 1, 2], ... [1, 2, 3], ... [0, 0, 0]], dtype='int32') >>> target = paddle.to_tensor([[100, 200, 300, 400], ... [500, 600, 700, 800], ... [900, 1000, 1100, 1200]], dtype='int32') >>> out_z1 = paddle.index_sample(x, index) >>> print(out_z1.numpy()) [[1. 2. 3.] [6. 7. 8.] [9. 9. 9.]] >>> # Use the index of the maximum value by topk op >>> # get the value of the element of the corresponding index in other tensors >>> top_value, top_index = paddle.topk(x, k=2) >>> out_z2 = paddle.index_sample(target, top_index) >>> print(top_value.numpy()) [[ 4. 3.] [ 8. 7.] [12. 11.]] >>> print(top_index.numpy()) [[3 2] [3 2] [3 2]] >>> print(out_z2.numpy()) [[ 400 300] [ 800 700] [1200 1100]]
-
index_select
(
index: Tensor,
axis: int = 0,
name: str | None = None,
*,
out: Tensor | None = None
)
Tensor
index_select¶
-
Returns a new tensor which indexes the
inputtensor along dimensionaxisusing the entries inindexwhich is a Tensor. The returned tensor has the same number of dimensions as the originalxtensor. The dim-th dimension has the same size as the length ofindex; other dimensions have the same size as in thextensor.Note
Alias and Order Support: 1. The parameter name
inputcan be used as an alias forx. 2. The parameter namedimcan be used as an alias foraxis. 3. This API also supports the PyTorch argument order(input, dim, index)for positional arguments, which will be converted to the Paddle order(x, index, axis). For example,paddle.index_select(input=x, dim=1, index=idx)is equivalent topaddle.index_select(x=x, axis=1, index=idx), andpaddle.index_select(x, 1, idx)is equivalent topaddle.index_select(x, idx, axis=1).- Parameters
-
x (Tensor) – The input Tensor to be operated. The data of
xcan be one of float16, float32, float64, int32, int64, complex64 and complex128. alias:input.index (Tensor) – The 1-D Tensor containing the indices to index. The data type of
indexmust be int32 or int64.axis (int, optional) – The dimension in which we index. Default: if None, the
axisis 0. alias:dim.name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Keyword Arguments
-
out (Tensor|None, optional) – The output tensor. Default: None.
- Returns
-
Tensor, A Tensor with same data type as
x.
Examples
>>> import paddle >>> x = paddle.to_tensor([[1.0, 2.0, 3.0, 4.0], ... [5.0, 6.0, 7.0, 8.0], ... [9.0, 10.0, 11.0, 12.0]]) >>> index = paddle.to_tensor([0, 1, 1], dtype='int32') >>> out_z1 = paddle.index_select(x=x, index=index) >>> print(out_z1.numpy()) [[1. 2. 3. 4.] [5. 6. 7. 8.] [5. 6. 7. 8.]] >>> out_z2 = paddle.index_select(x=x, index=index, axis=1) >>> print(out_z2.numpy()) [[ 1. 2. 2.] [ 5. 6. 6.] [ 9. 10. 10.]]
-
inner
(
y: Tensor,
name: str | None = None
)
Tensor
inner¶
-
Inner product of two input Tensor.
Ordinary inner product for 1-D Tensors, in higher dimensions a sum product over the last axes.
- Parameters
-
x (Tensor) – An N-D Tensor or a Scalar Tensor. If its not a scalar Tensor, its last dimensions must match y’s.
y (Tensor) – An N-D Tensor or a Scalar Tensor. If its not a scalar Tensor, its last dimensions must match x’s.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
The inner-product Tensor, the output shape is x.shape[:-1] + y.shape[:-1].
- Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.arange(1, 7).reshape((2, 3)).astype('float32') >>> y = paddle.arange(1, 10).reshape((3, 3)).astype('float32') >>> out = paddle.inner(x, y) >>> print(out) Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True, [[14. , 32. , 50. ], [32. , 77. , 122.]])
-
inverse
(
name: str | None = None
)
Tensor
inverse¶
-
Takes the inverse of the square matrix. A square matrix is a matrix with the same number of rows and columns. The input can be a square matrix (2-D Tensor) or batches of square matrices.
- Parameters
-
x (Tensor) – The input tensor. The last two dimensions should be equal. When the number of dimensions is greater than 2, it is treated as batches of square matrix. The data type can be float32, float64, complex64, complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
- A Tensor holds the inverse of x. The shape and data type
-
is the same as x.
- Return type
-
Tensor
Examples
>>> import paddle >>> mat = paddle.to_tensor([[2, 0], [0, 2]], dtype='float32') >>> inv = paddle.inverse(mat) >>> print(inv) Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True, [[0.50000000, 0. ], [0. , 0.50000000]])
-
is_complex
(
)
bool
is_complex¶
-
Return whether x is a tensor of complex data type(complex64 or complex128).
Alias Support: The parameter name
inputcan be used as an alias forx. For example,input=tensor_xis equivalent tox=tensor_x.- Parameters
-
x (Tensor) – The input tensor.
input – An alias for
x, with identical behavior.
- Returns
-
True if the data type of the input is complex data type, otherwise false.
- Return type
-
bool
Examples
>>> import paddle >>> x = paddle.to_tensor([1 + 2j, 3 + 4j]) >>> print(paddle.is_complex(x)) True >>> x = paddle.to_tensor([1.1, 1.2]) >>> print(paddle.is_complex(x)) False >>> x = paddle.to_tensor([1, 2, 3]) >>> print(paddle.is_complex(x)) False
-
is_contiguous
(
)
is_contiguous¶
-
Variable don’t have ‘is_contiguous’ interface in static graph mode But this interface can greatly facilitate dy2static. So we give a warning here and return None.
-
is_empty
(
name: str | None = None
)
Tensor
is_empty¶
-
Test whether a Tensor is empty.
- Parameters
-
x (Tensor) – The Tensor to be tested.
name (str|None, optional) – The default value is
None. Normally users don’t have to set this parameter. For more information, please refer to api_guide_Name .
- Returns
-
A bool scalar Tensor. True if ‘x’ is an empty Tensor.
- Return type
-
Tensor
Examples
>>> import paddle >>> input = paddle.rand(shape=[4, 32, 32], dtype='float32') >>> res = paddle.is_empty(x=input) >>> print(res) Tensor(shape=[], dtype=bool, place=Place(cpu), stop_gradient=True, False)
-
is_floating_point
(
)
bool
is_floating_point¶
-
Returns whether the dtype of x is one of paddle.float64, paddle.float32, paddle.float16, and paddle.bfloat16.
- Parameters
-
x (Tensor) – The input tensor.
- Returns
-
True if the dtype of x is floating type, otherwise false.
- Return type
-
bool
Examples
>>> import paddle >>> x = paddle.arange(1., 5., dtype='float32') >>> y = paddle.arange(1, 5, dtype='int32') >>> print(paddle.is_floating_point(x)) True >>> print(paddle.is_floating_point(y)) False
-
is_integer
(
)
bool
is_integer¶
-
Return whether x is a tensor of integral data type.
- Parameters
-
x (Tensor) – The input tensor.
- Returns
-
True if the data type of the input is integer data type, otherwise false.
- Return type
-
bool
Examples
>>> import paddle >>> x = paddle.to_tensor([1 + 2j, 3 + 4j]) >>> print(paddle.is_integer(x)) False >>> x = paddle.to_tensor([1.1, 1.2]) >>> print(paddle.is_integer(x)) False >>> x = paddle.to_tensor([1, 2, 3]) >>> print(paddle.is_integer(x)) True
-
is_tensor
(
)
TypeGuard[Tensor]
is_tensor¶
-
Tests whether input object is a paddle.Tensor.
- Parameters
-
x (object) – Object to test.
- Returns
-
A boolean value. True if
xis a paddle.Tensor, otherwise False.
Examples
>>> import paddle >>> input1 = paddle.rand(shape=[2, 3, 5], dtype='float32') >>> check = paddle.is_tensor(input1) >>> print(check) True >>> input3 = [1, 4] >>> check = paddle.is_tensor(input3) >>> print(check) False
-
isclose
(
y: Tensor,
rtol: float = 1e-05,
atol: float = 1e-08,
equal_nan: bool = False,
name: str | None = None
)
Tensor
isclose¶
-
Check if all \(x\) and \(y\) satisfy the condition:
\[\left| x - y \right| \leq atol + rtol \times \left| y \right|\]elementwise, for all elements of \(x\) and \(y\). The behaviour of this operator is analogous to \(numpy.isclose\), namely that it returns \(True\) if two tensors are elementwise equal within a tolerance.
- Parameters
-
x (Tensor) – The input tensor, it’s data type should be float16, float32, float64, complex64, complex128.
y (Tensor) – The input tensor, it’s data type should be float16, float32, float64, complex64, complex128.
rtol (float, optional) – The relative tolerance. Default: \(1e-5\) .
atol (float, optional) – The absolute tolerance. Default: \(1e-8\) .
equal_nan (bool, optional) – If \(True\) , then two \(NaNs\) will be compared as equal. Default: \(False\) .
name (str|None, optional) – Name for the operation. For more information, please refer to api_guide_Name. Default: None.
- Returns
-
The output tensor, it’s data type is bool.
- Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.to_tensor([10000., 1e-07]) >>> y = paddle.to_tensor([10000.1, 1e-08]) >>> result1 = paddle.isclose(x, y, rtol=1e-05, atol=1e-08, ... equal_nan=False, name="ignore_nan") >>> print(result1) Tensor(shape=[2], dtype=bool, place=Place(cpu), stop_gradient=True, [True , False]) >>> result2 = paddle.isclose(x, y, rtol=1e-05, atol=1e-08, ... equal_nan=True, name="equal_nan") >>> print(result2) Tensor(shape=[2], dtype=bool, place=Place(cpu), stop_gradient=True, [True , False]) >>> x = paddle.to_tensor([1.0, float('nan')]) >>> y = paddle.to_tensor([1.0, float('nan')]) >>> result1 = paddle.isclose(x, y, rtol=1e-05, atol=1e-08, ... equal_nan=False, name="ignore_nan") >>> print(result1) Tensor(shape=[2], dtype=bool, place=Place(cpu), stop_gradient=True, [True , False]) >>> result2 = paddle.isclose(x, y, rtol=1e-05, atol=1e-08, ... equal_nan=True, name="equal_nan") >>> print(result2) Tensor(shape=[2], dtype=bool, place=Place(cpu), stop_gradient=True, [True, True])
-
isfinite
(
)
isfinite¶
-
C++ interface function for isfinite.
-
isin
(
test_x: Tensor,
assume_unique: bool = False,
invert: bool = False,
name: str | None = None
)
Tensor
isin¶
-
Tests if each element of x is in test_x.
- Parameters
-
x (Tensor) – The input Tensor. Supported data type: ‘bfloat16’, ‘float16’, ‘float32’, ‘float64’, ‘int32’, ‘int64’.
test_x (Tensor) – Tensor values against which to test for each input element. Supported data type: ‘bfloat16’, ‘float16’, ‘float32’, ‘float64’, ‘int32’, ‘int64’.
assume_unique (bool, optional) – If True, indicates both x and test_x contain unique elements, which could make the calculation faster. Default: False.
invert (bool, optional) – Indicate whether to invert the boolean return tensor. If True, invert the results. Default: False.
name (str|None, optional) – Name for the operation (optional, default is None).For more information, please refer to api_guide_Name.
- Returns
-
out (Tensor), The output Tensor with the same shape as x.
Examples
>>> import paddle >>> paddle.set_device('cpu') >>> x = paddle.to_tensor([-0., -2.1, 2.5, 1.0, -2.1], dtype='float32') >>> test_x = paddle.to_tensor([-2.1, 2.5], dtype='float32') >>> res = paddle.isin(x, test_x) >>> print(res) Tensor(shape=[5], dtype=bool, place=Place(cpu), stop_gradient=True, [False, True, True, False, True]) >>> x = paddle.to_tensor([-0., -2.1, 2.5, 1.0, -2.1], dtype='float32') >>> test_x = paddle.to_tensor([-2.1, 2.5], dtype='float32') >>> res = paddle.isin(x, test_x, invert=True) >>> print(res) Tensor(shape=[5], dtype=bool, place=Place(cpu), stop_gradient=True, [True, False, False, True, False]) >>> # Set `assume_unique` to True only when `x` and `test_x` contain unique values, otherwise the result may be incorrect. >>> x = paddle.to_tensor([0., 1., 2.]*20).reshape([20, 3]) >>> test_x = paddle.to_tensor([0., 1.]*20) >>> correct_result = paddle.isin(x, test_x, assume_unique=False) >>> print(correct_result) Tensor(shape=[20, 3], dtype=bool, place=Place(cpu), stop_gradient=True, [[True , True , False], [True , True , False], [True , True , False], [True , True , False], [True , True , False], [True , True , False], [True , True , False], [True , True , False], [True , True , False], [True , True , False], [True , True , False], [True , True , False], [True , True , False], [True , True , False], [True , True , False], [True , True , False], [True , True , False], [True , True , False], [True , True , False], [True , True , False]]) >>> incorrect_result = paddle.isin(x, test_x, assume_unique=True) >>> print(incorrect_result) Tensor(shape=[20, 3], dtype=bool, place=Place(gpu:0), stop_gradient=True, [[True , True , True ], [True , True , True ], [True , True , True ], [True , True , True ], [True , True , True ], [True , True , True ], [True , True , True ], [True , True , True ], [True , True , True ], [True , True , True ], [True , True , True ], [True , True , True ], [True , True , True ], [True , True , True ], [True , True , True ], [True , True , True ], [True , True , True ], [True , True , True ], [True , True , True ], [True , True , False]])
-
isinf
(
)
isinf¶
-
C++ interface function for isinf.
-
isnan
(
)
isnan¶
-
C++ interface function for isnan.
-
isneginf
(
name: str | None = None
)
Tensor
isneginf¶
-
Tests if each element of input is negative infinity or not.
- Parameters
-
x (Tensor) – The input Tensor. Must be one of the following types: bfloat16, float16, float32, float64, int8, int16, int32, int64, uint8.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
out (Tensor), The output Tensor. Each element of output indicates whether the input element is negative infinity or not.
Examples
>>> import paddle >>> paddle.set_device('cpu') >>> x = paddle.to_tensor([-0., float('inf'), -2.1, -float('inf'), 2.5], dtype='float32') >>> res = paddle.isneginf(x) >>> print(res) Tensor(shape=[5], dtype=bool, place=Place(cpu), stop_gradient=True, [False, False, False, True, False])
-
isposinf
(
name: str | None = None
)
Tensor
isposinf¶
-
Tests if each element of input is positive infinity or not.
- Parameters
-
x (Tensor) – The input Tensor. Must be one of the following types: bfloat16, float16, float32, float64, int8, int16, int32, int64, uint8.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
out (Tensor), The output Tensor. Each element of output indicates whether the input element is positive infinity or not.
Examples
>>> import paddle >>> paddle.set_device('cpu') >>> x = paddle.to_tensor([-0., float('inf'), -2.1, -float('inf'), 2.5], dtype='float32') >>> res = paddle.isposinf(x) >>> print(res) Tensor(shape=[5], dtype=bool, place=Place(cpu), stop_gradient=True, [False, True, False, False, False])
-
isreal
(
name: str | None = None
)
Tensor
isreal¶
-
Tests if each element of input is a real number or not.
- Parameters
-
x (Tensor) – The input Tensor.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
out (Tensor), The output Tensor. Each element of output indicates whether the input element is a real number or not.
Examples
>>> import paddle >>> paddle.set_device('cpu') >>> x = paddle.to_tensor([-0., -2.1, 2.5], dtype='float32') >>> res = paddle.isreal(x) >>> print(res) Tensor(shape=[3], dtype=bool, place=Place(cpu), stop_gradient=True, [True, True, True]) >>> x = paddle.to_tensor([(-0.+1j), (-2.1+0.2j), (2.5-3.1j)]) >>> res = paddle.isreal(x) >>> print(res) Tensor(shape=[3], dtype=bool, place=Place(cpu), stop_gradient=True, [False, False, False]) >>> x = paddle.to_tensor([(-0.+1j), (-2.1+0j), (2.5-0j)]) >>> res = paddle.isreal(x) >>> print(res) Tensor(shape=[3], dtype=bool, place=Place(cpu), stop_gradient=True, [False, True, True])
-
istft
(
n_fft: int,
hop_length: int | None = None,
win_length: int | None = None,
window: Tensor | None = None,
center: bool = True,
normalized: bool = False,
onesided: bool = True,
length: int | None = None,
return_complex: bool = False,
name: str | None = None
)
Tensor
istft¶
-
Inverse short-time Fourier transform (ISTFT).
Reconstruct time-domain signal from the giving complex input and window tensor when nonzero overlap-add (NOLA) condition is met:
\[\sum_{t = -\infty}^{\infty} \text{window}^2[n - t \times H]\ \neq \ 0, \ \text{for } all \ n\]Where: - \(t\): The \(t\)-th input window. - \(N\): Value of n_fft. - \(H\): Value of hop_length.
Result of istft expected to be the inverse of paddle.signal.stft, but it is not guaranteed to reconstruct a exactly realizable time-domain signal from a STFT complex tensor which has been modified (via masking or otherwise). Therefore, istft gives the [Griffin-Lim optimal estimate] (optimal in a least-squares sense) for the corresponding signal.
- Parameters
-
x (Tensor) – The input data which is a 2-dimensional or 3-dimensional complex Tensor with shape […, n_fft, num_frames].
n_fft (int) – The size of Fourier transform.
hop_length (int|None, optional) – Number of steps to advance between adjacent windows from time-domain signal and 0 < hop_length < win_length. Default: None ( treated as equal to n_fft//4)
win_length (int|None, optional) – The size of window. Default: None (treated as equal to n_fft)
window (Tensor|None, optional) – A 1-dimensional tensor of size win_length. It will be center padded to length n_fft if win_length < n_fft. It should be a real-valued tensor if return_complex is False. Default: None`(treated as a rectangle window with value equal to 1 of size `win_length).
center (bool, optional) – It means that whether the time-domain signal has been center padded. Default: True.
normalized (bool, optional) – Control whether to scale the output by \(1/sqrt(n_{fft})\). Default: False
onesided (bool, optional) – It means that whether the input STFT tensor is a half of the conjugate symmetry STFT tensor transformed from a real-valued signal and istft will return a real-valued tensor when it is set to True. Default: True.
length (int|None, optional) – Specify the length of time-domain signal. Default: `None`( treated as the whole length of signal).
return_complex (bool, optional) – It means that whether the time-domain signal is real-valued. If return_complex is set to True, onesided should be set to False cause the output is complex.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
- Returns
-
A tensor of least squares estimation of the reconstructed signal(s) with shape […, seq_length]
Examples
>>> import numpy as np >>> import paddle >>> from paddle.signal import stft, istft >>> paddle.seed(0) >>> # STFT >>> x = paddle.randn([8, 48000], dtype=paddle.float64) >>> y = stft(x, n_fft=512) >>> print(y.shape) [8, 257, 376] >>> # ISTFT >>> x_ = istft(y, n_fft=512) >>> print(x_.shape) [8, 48000] >>> np.allclose(x, x_) True
-
item
(
)
item¶
-
In order to be compatible with the item interface introduced by the dynamic graph, it does nothing but returns self. It will check that the shape must be a 1-D tensor
-
kron
(
y: Tensor,
name: str | None = None
)
Tensor
kron¶
-
Compute the Kronecker product of two tensors, a composite tensor made of blocks of the second tensor scaled by the first. Assume that the rank of the two tensors, $X$ and $Y$ are the same, if necessary prepending the smallest with ones. If the shape of $X$ is [$r_0$, $r_1$, …, $r_N$] and the shape of $Y$ is [$s_0$, $s_1$, …, $s_N$], then the shape of the output tensor is [$r_{0}s_{0}$, $r_{1}s_{1}$, …, $r_{N}s_{N}$]. The elements are products of elements from $X$ and $Y$. The equation is: $$ output[k_{0}, k_{1}, …, k_{N}] = X[i_{0}, i_{1}, …, i_{N}] * Y[j_{0}, j_{1}, …, j_{N}] $$ where $$ k_{t} = i_{t} * s_{t} + j_{t}, t = 0, 1, …, N $$
- Parameters
-
x (Tensor) – the fist operand of kron op, data type: bfloat16, float16, float32, float64, int32 or int64.
y (Tensor) – the second operand of kron op, data type: bfloat16, float16, float32, float64, int32 or int64. Its data type should be the same with x.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
The output of kron, data type: bfloat16, float16, float32, float64, int32 or int64. Its data is the same with x.
- Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.to_tensor([[1, 2], [3, 4]], dtype='int64') >>> y = paddle.to_tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9]], dtype='int64') >>> out = paddle.kron(x, y) >>> out Tensor(shape=[6, 6], dtype=int64, place=Place(cpu), stop_gradient=True, [[1 , 2 , 3 , 2 , 4 , 6 ], [4 , 5 , 6 , 8 , 10, 12], [7 , 8 , 9 , 14, 16, 18], [3 , 6 , 9 , 4 , 8 , 12], [12, 15, 18, 16, 20, 24], [21, 24, 27, 28, 32, 36]])
-
kthvalue
(
k: int,
axis: int | None = None,
keepdim: bool = False,
name: str | None = None
)
tuple[Tensor, Tensor]
kthvalue¶
-
Find values and indices of the k-th smallest at the axis.
- Parameters
-
x (Tensor) – A N-D Tensor with type float16, float32, float64, int32, int64.
k (int) – The k for the k-th smallest number to look for along the axis.
axis (int, optional) – Axis to compute indices along. The effective range is [-R, R), where R is x.ndim. when axis < 0, it works the same way as axis + R. The default is None. And if the axis is None, it will computed as -1 by default.
keepdim (bool, optional) – Whether to keep the given axis in output. If it is True, the dimensions will be same as input x and with size one in the axis. Otherwise the output dimensions is one fewer than x since the axis is squeezed. Default is False.
name (str, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Returns
-
tuple(Tensor), return the values and indices. The value data type is the same as the input x. The indices data type is int64.
Examples
>>> import paddle >>> x = paddle.randn((2,3,2)) >>> print(x) >>> Tensor(shape=[2, 3, 2], dtype=float32, place=Place(cpu), stop_gradient=True, [[[ 0.11855337, -0.30557564], [-0.09968963, 0.41220093], [ 1.24004936, 1.50014710]], [[ 0.08612321, -0.92485696], [-0.09276631, 1.15149164], [-1.46587241, 1.22873247]]]) >>> >>> y = paddle.kthvalue(x, 2, 1) >>> print(y) >>> (Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True, [[ 0.11855337, 0.41220093], [-0.09276631, 1.15149164]]), Tensor(shape=[2, 2], dtype=int64, place=Place(cpu), stop_gradient=True, [[0, 1], [1, 1]])) >>>
-
lcm
(
y: Tensor,
name: str | None = None
)
Tensor
lcm¶
-
Computes the element-wise least common multiple (LCM) of input |x| and |y|. Both x and y must have integer types.
Note
lcm(0,0)=0, lcm(0, y)=0
If x.shape != y.shape, they must be broadcastable to a common shape (which becomes the shape of the output).
- Parameters
-
x (Tensor) – An N-D Tensor, the data type is int32, int64.
y (Tensor) – An N-D Tensor, the data type is int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
An N-D Tensor, the data type is the same with input.
- Return type
-
out (Tensor)
Examples
>>> import paddle >>> x1 = paddle.to_tensor(12) >>> x2 = paddle.to_tensor(20) >>> paddle.lcm(x1, x2) Tensor(shape=[], dtype=int64, place=Place(cpu), stop_gradient=True, 60) >>> x3 = paddle.arange(6) >>> paddle.lcm(x3, x2) Tensor(shape=[6], dtype=int64, place=Place(cpu), stop_gradient=True, [0, 20, 20, 60, 20, 20]) >>> x4 = paddle.to_tensor(0) >>> paddle.lcm(x4, x2) Tensor(shape=[], dtype=int64, place=Place(cpu), stop_gradient=True, 0) >>> paddle.lcm(x4, x4) Tensor(shape=[], dtype=int64, place=Place(cpu), stop_gradient=True, 0) >>> x5 = paddle.to_tensor(-20) >>> paddle.lcm(x1, x5) Tensor(shape=[], dtype=int64, place=Place(cpu), stop_gradient=True, 60)
-
lcm_
(
y: Tensor,
name: str | None = None
)
Tensor
lcm_¶
-
Inplace version of
lcmAPI, the output Tensor will be inplaced with inputx. Please refer to lcm.
-
ldexp
(
y: Tensor,
name: str | None = None
)
Tensor
ldexp¶
-
Compute the result of multiplying x by 2 to the power of y. The equation is:
\[out = x * 2^{y}\]- Parameters
-
x (Tensor) – The input Tensor, the data type is float32, float64, int32 or int64.
y (Tensor) – A Tensor of exponents, typically integers.
name (str|None, optional) – Name for the operation (optional, default is None).For more information, please refer to api_guide_Name.
- Returns
-
An N-D Tensor. If x, y have different shapes and are “broadcastable”, the resulting tensor shape is the shape of x and y after broadcasting. If x, y have the same shape, its shape is the same as x and y. And the data type is float32 or float64.
- Return type
-
out (Tensor)
Examples
>>> import paddle >>> # example1 >>> x = paddle.to_tensor([1, 2, 3], dtype='float32') >>> y = paddle.to_tensor([2, 3, 4], dtype='int32') >>> res = paddle.ldexp(x, y) >>> print(res) Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True, [4. , 16., 48.]) >>> # example2 >>> x = paddle.to_tensor([1, 2, 3], dtype='float32') >>> y = paddle.to_tensor([2], dtype='int32') >>> res = paddle.ldexp(x, y) >>> print(res) Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True, [4. , 8. , 12.])
-
ldexp_
(
y: Tensor,
name: str | None = None
)
Tensor
ldexp_¶
-
Inplace version of
polygammaAPI, the output Tensor will be inplaced with inputx. Please refer to polygamma.
-
lerp
(
y: Tensor,
weight: float | Tensor,
name: str | None = None
)
Tensor
lerp¶
-
Does a linear interpolation between x and y based on weight.
- Equation:
-
\[lerp(x, y, weight) = x + weight * (y - x).\]
- Parameters
-
x (Tensor) – An N-D Tensor with starting points, the data type is bfloat16, float16, float32, float64.
y (Tensor) – An N-D Tensor with ending points, the data type is bfloat16, float16, float32, float64.
weight (float|Tensor) – The weight for the interpolation formula. When weight is Tensor, the data type is bfloat16, float16, float32, float64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
An N-D Tensor, the shape and data type is the same with input.
- Return type
-
out (Tensor)
Example
>>> import paddle >>> x = paddle.arange(1., 5., dtype='float32') >>> y = paddle.empty([4], dtype='float32') >>> y.fill_(10.) >>> out = paddle.lerp(x, y, 0.5) >>> out Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [5.50000000, 6. , 6.50000000, 7. ])
-
lerp_
(
y: Tensor,
weight: float | Tensor,
name: str | None = None
)
Tensor
lerp_¶
-
Inplace version of
lerpAPI, the output Tensor will be inplaced with inputx. Please refer to lerp.
-
less
(
y: Tensor,
name: str | None = None
)
Tensor
less¶
-
Returns the truth value of \(x < y\) elementwise, which is equivalent function to the overloaded operator <.
Note
The output has no gradient.
- Parameters
-
x (Tensor) – First input to compare which is N-D tensor. The input data type should be bool, bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64.
y (Tensor) – Second input to compare which is N-D tensor. The input data type should be bool, bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
- Returns
-
The output shape is same as input
x. The output data type is bool. - Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.to_tensor([1, 2, 3]) >>> y = paddle.to_tensor([1, 3, 2]) >>> result1 = paddle.less(x, y) >>> print(result1) Tensor(shape=[3], dtype=bool, place=Place(cpu), stop_gradient=True, [False, True , False])
-
less_
(
y: Tensor,
name: str | None = None
)
Tensor
less_¶
-
Inplace version of
less_API, the output Tensor will be inplaced with inputx. Please refer to less.
-
less_equal
(
y: Tensor,
name: str | None = None
)
Tensor
less_equal¶
-
Returns the truth value of \(x <= y\) elementwise, which is equivalent function to the overloaded operator <=.
Note
The output has no gradient.
- Parameters
-
x (Tensor) – First input to compare which is N-D tensor. The input data type should be bool, bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64, complex64, complex128.
y (Tensor) – Second input to compare which is N-D tensor. The input data type should be bool, bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64, complex64, complex128.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
- Returns
-
The output shape is same as input
x. The output data type is bool. - Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.to_tensor([1, 2, 3]) >>> y = paddle.to_tensor([1, 3, 2]) >>> result1 = paddle.less_equal(x, y) >>> print(result1) Tensor(shape=[3], dtype=bool, place=Place(cpu), stop_gradient=True, [True , True , False])
-
less_equal_
(
y: Tensor,
name: str | None = None
)
Tensor
less_equal_¶
-
Inplace version of
less_equalAPI, the output Tensor will be inplaced with inputx. Please refer to less_equal.
-
less_than
(
y: Tensor,
name: str | None = None
)
Tensor
less_than¶
-
Returns the truth value of \(x < y\) elementwise, which is equivalent function to the overloaded operator <.
Note
The output has no gradient.
- Parameters
-
x (Tensor) – First input to compare which is N-D tensor. The input data type should be bool, bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64, complex64, complex128.
y (Tensor) – Second input to compare which is N-D tensor. The input data type should be bool, bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64, complex64, complex128.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
- Returns
-
The output shape is same as input
x. The output data type is bool. - Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.to_tensor([1, 2, 3]) >>> y = paddle.to_tensor([1, 3, 2]) >>> result1 = paddle.less_than(x, y) >>> print(result1) Tensor(shape=[3], dtype=bool, place=Place(cpu), stop_gradient=True, [False, True , False])
-
less_than_
(
y: Tensor,
name: str | None = None
)
Tensor
less_than_¶
-
Inplace version of
less_thanAPI, the output Tensor will be inplaced with inputx. Please refer to less_than.
-
lgamma
(
name: str | None = None
)
Tensor
lgamma¶
-
Calculates the lgamma of the given input tensor, element-wise.
This operator performs elementwise lgamma for input $X$. \(out = log\Gamma(x)\)
- Parameters
-
x (Tensor) – Input Tensor. Must be one of the following types: bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
- Tensor, the lgamma of the input Tensor, the shape and data type is the same with input
-
(integer types are autocasted into float32).
Examples
>>> import paddle >>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3]) >>> out = paddle.lgamma(x) >>> out Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [1.31452453, 1.76149762, 2.25271273, 1.09579790])
-
lgamma_
(
name: str | None = None
)
Tensor
lgamma_¶
-
Inplace version of
lgammaAPI, the output Tensor will be inplaced with inputx. Please refer to lgamma.
-
log
(
)
log¶
-
C++ interface function for log.
-
log10
(
name: str | None = None
)
Tensor
log10¶
-
Calculates the log to the base 10 of the given input tensor, element-wise.
\[Out = \log_10_x\]- Parameters
-
x (Tensor) – Input tensor must be one of the following types: int32, int64, float16, bfloat16, float32, float64, complex64, complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
The log to the base 10 of the input Tensor computed element-wise.
- Return type
-
Tensor
Examples
>>> import paddle >>> # example 1: x is a float >>> x_i = paddle.to_tensor([[1.0], [10.0]]) >>> res = paddle.log10(x_i) >>> res Tensor(shape=[2, 1], dtype=float32, place=Place(cpu), stop_gradient=True, [[0.], [1.]]) >>> # example 2: x is float32 >>> x_i = paddle.full(shape=[1], fill_value=10, dtype='float32') >>> paddle.to_tensor(x_i) >>> res = paddle.log10(x_i) >>> res Tensor(shape=[1], dtype=float32, place=Place(cpu), stop_gradient=True, [1.]) >>> # example 3: x is float64 >>> x_i = paddle.full(shape=[1], fill_value=10, dtype='float64') >>> paddle.to_tensor(x_i) >>> res = paddle.log10(x_i) >>> res Tensor(shape=[1], dtype=float64, place=Place(cpu), stop_gradient=True, [1.])
-
log10_
(
name: str | None = None
)
Tensor
log10_¶
-
Inplace version of
log10API, the output Tensor will be inplaced with inputx. Please refer to log10.
-
log1p
(
name: str | None = None
)
Tensor
log1p¶
-
Calculates the natural log of the given input tensor, element-wise.
\[Out = \ln(x+1)\]- Parameters
-
x (Tensor) – Input Tensor. Must be one of the following types: int32, int64, float16, bfloat16, float32, float64, complex64, complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, the natural log of the input Tensor computed element-wise.
Examples
>>> import paddle >>> data = paddle.to_tensor([[0], [1]], dtype='float32') >>> res = paddle.log1p(data) >>> res Tensor(shape=[2, 1], dtype=float32, place=Place(cpu), stop_gradient=True, [[0. ], [0.69314718]])
-
log1p_
(
name: str | None = None
)
None
log1p_¶
-
Inplace version of
log1pAPI, the output Tensor will be inplaced with inputx. Please refer to log1p.
-
log2
(
name: str | None = None
)
Tensor
log2¶
-
Calculates the log to the base 2 of the given input tensor, element-wise.
\[Out = \log_2x\]- Parameters
-
x (Tensor) – Input tensor must be one of the following types: int32, int64, float16, bfloat16, float32, float64, complex64, complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
The log to the base 2 of the input Tensor computed element-wise.
- Return type
-
Tensor
Examples
>>> import paddle >>> # example 1: x is a float >>> x_i = paddle.to_tensor([[1.0], [2.0]]) >>> res = paddle.log2(x_i) >>> res Tensor(shape=[2, 1], dtype=float32, place=Place(cpu), stop_gradient=True, [[0.], [1.]]) >>> # example 2: x is float32 >>> x_i = paddle.full(shape=[1], fill_value=2, dtype='float32') >>> paddle.to_tensor(x_i) >>> res = paddle.log2(x_i) >>> res Tensor(shape=[1], dtype=float32, place=Place(cpu), stop_gradient=True, [1.]) >>> # example 3: x is float64 >>> x_i = paddle.full(shape=[1], fill_value=2, dtype='float64') >>> paddle.to_tensor(x_i) >>> res = paddle.log2(x_i) >>> res Tensor(shape=[1], dtype=float64, place=Place(cpu), stop_gradient=True, [1.])
-
log2_
(
name: str | None = None
)
Tensor
log2_¶
-
Inplace version of
log2API, the output Tensor will be inplaced with inputx. Please refer to log2.
-
log_
(
name: str | None = None
)
Tensor
log_¶
-
Inplace version of
logAPI, the output Tensor will be inplaced with inputx. Please refer to log.
-
log_normal_
(
mean: float = 1.0,
std: float = 2.0,
name: str | None = None
)
Tensor
log_normal_¶
-
This inplace version of api
log_normal, which returns a Tensor filled with random values sampled from a log normal distribution. The output Tensor will be inplaced with inputx. Please refer to log_normal.- Parameters
-
x (Tensor) – The input tensor to be filled with random values.
mean (float|int, optional) – Mean of the output tensor, default is 1.0.
std (float|int, optional) – Standard deviation of the output tensor, default is 2.0.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
- Returns
-
Tensor, A Tensor filled with random values sampled from a log normal distribution with the underlying normal distribution’s
meanandstd.
Examples
>>> import paddle >>> paddle.seed(200) >>> x = paddle.randn([3, 4]) >>> x.log_normal_() >>> print(x) Tensor(shape=[3, 4], dtype=float32, place=Place(cpu), stop_gradient=True, [[3.99360156 , 0.11746082 , 12.14813519, 4.74383831 ], [0.36592522 , 0.09426476 , 31.81549835, 0.61839998 ], [1.33314908 , 12.31954002, 36.44527435, 1.69572163 ]])
-
logaddexp
(
y: Tensor,
name: str | None = None
)
Tensor
logaddexp¶
-
Elementwise LogAddExp Operator. Add of exponentiations of the inputs The equation is:
\[Out=log(X.exp()+Y.exp())\]$X$ the tensor of any dimension. $Y$ the tensor whose dimensions must be less than or equal to the dimensions of $X$.
There are two cases for this operator:
The shape of $Y$ is the same with $X$.
The shape of $Y$ is a continuous subsequence of $X$.
For case 2:
Broadcast $Y$ to match the shape of $X$, where axis is the start dimension index for broadcasting $Y$ onto $X$.
If $axis$ is -1 (default), $axis$=rank($X$)-rank($Y$).
The trailing dimensions of size 1 for $Y$ will be ignored for the consideration of subsequence, such as shape($Y$) = (2, 1) => (2).
For example:
shape(X) = (2, 3, 4, 5), shape(Y) = (,) shape(X) = (2, 3, 4, 5), shape(Y) = (5,) shape(X) = (2, 3, 4, 5), shape(Y) = (4, 5), with axis=-1(default) or axis=2 shape(X) = (2, 3, 4, 5), shape(Y) = (3, 4), with axis=1 shape(X) = (2, 3, 4, 5), shape(Y) = (2), with axis=0 shape(X) = (2, 3, 4, 5), shape(Y) = (2, 1), with axis=0
- Parameters
-
x (Tensor) – Tensor of any dimensions. Its dtype should be int32, int64, bfloat16, float16, float32, float64.
y (Tensor) – Tensor of any dimensions. Its dtype should be int32, int64, bfloat16, float16, float32, float64.
name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Returns
-
N-D Tensor. A location into which the result is stored. It’s dimension equals with x.
Examples
>>> import paddle >>> x = paddle.to_tensor([-1, -2, -3], 'float64') >>> y = paddle.to_tensor([-1], 'float64') >>> z = paddle.logaddexp(x, y) >>> print(z) Tensor(shape=[3], dtype=float64, place=Place(cpu), stop_gradient=True, [-0.30685282, -0.68673831, -0.87307199])
-
logcumsumexp
(
axis: int | None = None,
dtype: DTypeLike | None = None,
name: str | None = None
)
Tensor
logcumsumexp¶
-
The logarithm of the cumulative summation of the exponentiation of the elements along a given axis.
For summation index j given by axis and other indices i, the result is
\[logcumsumexp(x)_{ij} = log \sum_{i=0}^{j}exp(x_{ij})\]Note
The first element of the result is the same as the first element of the input.
- Parameters
-
x (Tensor) – The input tensor, with data type float32, float64, float16, bfloat16, uint8, int8, int16, int32, int64
axis (int, optional) – The dimension to do the operation along. -1 means the last dimension. The default (None) is to compute the cumsum over the flattened array.
dtype (str|core.VarDesc.VarType|core.DataType|np.dtype, optional) – The data type of the output tensor, can be float16, float32, float64. If specified, the input tensor is casted to dtype before the operation is performed. This is useful for preventing data type overflows. The default value is None.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, the result of logcumsumexp operator (integer input types are autocasted into float32).
Examples
>>> import paddle >>> data = paddle.arange(12, dtype='float64') >>> data = paddle.reshape(data, (3, 4)) >>> y = paddle.logcumsumexp(data) >>> y Tensor(shape=[12], dtype=float64, place=Place(cpu), stop_gradient=True, [0. , 1.31326169 , 2.40760596 , 3.44018970 , 4.45191440 , 5.45619332 , 6.45776285 , 7.45833963 , 8.45855173 , 9.45862974 , 10.45865844, 11.45866900]) >>> y = paddle.logcumsumexp(data, axis=0) >>> y Tensor(shape=[3, 4], dtype=float64, place=Place(cpu), stop_gradient=True, [[0. , 1. , 2. , 3. ], [4.01814993 , 5.01814993 , 6.01814993 , 7.01814993 ], [8.01847930 , 9.01847930 , 10.01847930, 11.01847930]]) >>> y = paddle.logcumsumexp(data, axis=-1) >>> y Tensor(shape=[3, 4], dtype=float64, place=Place(cpu), stop_gradient=True, [[0. , 1.31326169 , 2.40760596 , 3.44018970 ], [4. , 5.31326169 , 6.40760596 , 7.44018970 ], [8. , 9.31326169 , 10.40760596, 11.44018970]]) >>> y = paddle.logcumsumexp(data, dtype='float64') >>> assert y.dtype == paddle.float64
-
logical_and
(
)
logical_and¶
-
C++ interface function for logical_and.
-
logical_and_
(
y: Tensor,
name: str | None = None
)
Tensor
logical_and_¶
-
Inplace version of
logical_andAPI, the output Tensor will be inplaced with inputx. Please refer to logical_and.
-
logical_not
(
)
logical_not¶
-
C++ interface function for logical_not.
-
logical_not_
(
name: str | None = None
)
Tensor
logical_not_¶
-
Inplace version of
logical_notAPI, the output Tensor will be inplaced with inputx. Please refer to logical_not.
-
logical_or
(
)
logical_or¶
-
C++ interface function for logical_or.
-
logical_or_
(
y: Tensor,
name: str | None = None
)
Tensor
logical_or_¶
-
Inplace version of
logical_orAPI, the output Tensor will be inplaced with inputx. Please refer to logical_or.
-
logical_xor
(
)
logical_xor¶
-
C++ interface function for logical_xor.
-
logical_xor_
(
y: Tensor,
name: str | None = None
)
Tensor
logical_xor_¶
-
Inplace version of
logical_xorAPI, the output Tensor will be inplaced with inputx. Please refer to logical_xor.
-
logit
(
eps: float | None = None,
name: str | None = None
)
Tensor
logit¶
-
This function generates a new tensor with the logit of the elements of input x. x is clamped to [eps, 1-eps] when eps is not zero. When eps is zero and x < 0 or x > 1, the function will yields NaN.
\[logit(x) = ln(\frac{x}{1 - x})\]where
\[\begin{split}x_i= \left\{\begin{array}{rcl} x_i & &\text{if } eps == Default \\ eps & &\text{if } x_i < eps \\ x_i & &\text{if } eps <= x_i <= 1-eps \\ 1-eps & &\text{if } x_i > 1-eps \end{array}\right.\end{split}\]- Parameters
-
x (Tensor) – The input Tensor with data type bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64.
eps (float|None, optional) – the epsilon for input clamp bound. Default is None.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
-
A Tensor with the same data type and shape as
x -
(integer types are autocasted into float32).
-
A Tensor with the same data type and shape as
- Return type
-
out(Tensor)
Examples
>>> import paddle >>> x = paddle.to_tensor([0.2635, 0.0106, 0.2780, 0.2097, 0.8095]) >>> out1 = paddle.logit(x) >>> out1 Tensor(shape=[5], dtype=float32, place=Place(cpu), stop_gradient=True, [-1.02785587, -4.53624487, -0.95440406, -1.32673466, 1.44676447])
-
logit_
(
eps: float | None = None,
name: str | None = None
)
Tensor
logit_¶
-
Inplace version of
logitAPI, the output Tensor will be inplaced with inputx. Please refer to logit.
-
logsumexp
(
)
logsumexp¶
-
C++ interface function for logsumexp.
-
lstsq
(
y: Tensor,
rcond: float | None = None,
driver: Literal['gels', 'gelsy', 'gelsd', 'gelss'] | None = None,
name: str | None = None
)
tuple[Tensor, Tensor, Tensor, Tensor]
lstsq¶
-
Computes a solution to the least squares problem of a system of linear equations.
- Parameters
-
x (Tensor) – A tensor with shape
(*, M, N), the data type of the input Tensorxshould be one of float32, float64.y (Tensor) – A tensor with shape
(*, M, K), the data type of the input Tensoryshould be one of float32, float64.rcond (float, optional) – The default value is None. A float pointing number used to determine the effective rank of
x. Ifrcondis None, it will be set to max(M, N) times the machine precision of x_dtype.driver (str, optional) – The default value is None. The name of LAPACK method to be used. For CPU inputs the valid values are ‘gels’, ‘gelsy’, ‘gelsd, ‘gelss’. For CUDA input, the only valid driver is ‘gels’. If
driveris None, ‘gelsy’ is used for CPU inputs and ‘gels’ for CUDA inputs.name (str, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
- Returns
-
A tuple of 4 Tensors which is (
solution,residuals,rank,singular_values).solutionis a tensor with shape(*, N, K), meaning the least squares solution.residualsis a tensor with shape(*, K), meaning the squared residuals of the solutions, which is computed when M > N and every matrix inxis full-rank, otherwise return an empty tensor.rankis a tensor with shape(*), meaning the ranks of the matrices inx, which is computed whendriverin (‘gelsy’, ‘gelsd’, ‘gelss’), otherwise return an empty tensor.singular_valuesis a tensor with shape(*, min(M, N)), meaning singular values of the matrices inx, which is computed whendriverin (‘gelsd’, ‘gelss’), otherwise return an empty tensor. - Return type
-
Tuple
Examples
>>> import paddle >>> x = paddle.to_tensor([[1, 3], [3, 2], [5, 6.]]) >>> y = paddle.to_tensor([[3, 4, 6], [5, 3, 4], [1, 2, 1.]]) >>> results = paddle.linalg.lstsq(x, y, driver="gelsd") >>> print(results[0]) Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True, [[ 0.78350395, -0.22165027, -0.62371236], [-0.11340097, 0.78866047, 1.14948535]]) >>> print(results[1]) Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True, [19.81443405, 10.43814468, 30.56185532]) >>> print(results[2]) Tensor(shape=[], dtype=int32, place=Place(cpu), stop_gradient=True, 2) >>> print(results[3]) Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True, [9.03455734, 1.54167950]) >>> x = paddle.to_tensor([[10, 2, 3], [3, 10, 5], [5, 6, 12.]]) >>> y = paddle.to_tensor([[4, 2, 9], [2, 0, 3], [2, 5, 3.]]) >>> results = paddle.linalg.lstsq(x, y, driver="gels") >>> print(results[0]) Tensor(shape=[3, 3], dtype=float32, place=Place(cpu), stop_gradient=True, [[ 0.39386186, 0.10230169, 0.93606132], [ 0.10741688, -0.29028130, 0.11892584], [-0.05115093, 0.51918161, -0.19948851]]) >>> print(results[1]) Tensor(shape=[0], dtype=float32, place=Place(cpu), stop_gradient=True, [])
-
lu
(
pivot=True,
get_infos=False,
name=None
)
tuple[Tensor, Tensor] | tuple[Tensor, Tensor, Tensor]
lu¶
-
Computes the LU factorization of an N-D(N>=2) matrix x.
Returns the LU factorization(inplace x) and Pivots. low triangular matrix L and upper triangular matrix U are combined to a single LU matrix.
Pivoting is done if pivot is set to True. P mat can be get by pivots:
ones = eye(rows) #eye matrix of rank rows for i in range(cols): swap(ones[i], ones[pivots[i]]) return ones- Parameters
-
X (Tensor) – the tensor to factor of N-dimensions(N>=2). Its data type should be float32, float64, complex64, or complex128.
pivot (bool, optional) – controls whether pivoting is done. Default: True.
get_infos (bool, optional) – if set to True, returns an info IntTensor. Default: False.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
factorization (Tensor), LU matrix, the factorization of input X.
pivots (IntTensor), the pivots of size(*(N-2), min(m,n)). pivots stores all the intermediate transpositions of rows. The final permutation perm could be reconstructed by this, details refer to upper example.
infos (IntTensor, optional), if get_infos is True, this is a tensor of size (*(N-2)) where non-zero values indicate whether factorization for the matrix or each minibatch has succeeded or failed.
Examples
>>> import paddle >>> x = paddle.to_tensor([[1.0, 2.0], [3.0, 4.0], [5.0, 6.0]]).astype('float64') >>> lu,p,info = paddle.linalg.lu(x, get_infos=True) >>> print(lu) Tensor(shape=[3, 2], dtype=float64, place=Place(cpu), stop_gradient=True, [[5. , 6. ], [0.20000000, 0.80000000], [0.60000000, 0.50000000]]) >>> print(p) Tensor(shape=[2], dtype=int32, place=Place(cpu), stop_gradient=True, [3, 3]) >>> print(info) Tensor(shape=[], dtype=int32, place=Place(cpu), stop_gradient=True, 0) >>> P,L,U = paddle.linalg.lu_unpack(lu,p) >>> print(P) Tensor(shape=[3, 3], dtype=float64, place=Place(cpu), stop_gradient=True, [[0., 1., 0.], [0., 0., 1.], [1., 0., 0.]]) >>> print(L) Tensor(shape=[3, 2], dtype=float64, place=Place(cpu), stop_gradient=True, [[1. , 0. ], [0.20000000, 1. ], [0.60000000, 0.50000000]]) >>> print(U) Tensor(shape=[2, 2], dtype=float64, place=Place(cpu), stop_gradient=True, [[5. , 6. ], [0. , 0.80000000]]) >>> # one can verify : X = P @ L @ U ;
-
lu_unpack
(
y: Tensor,
unpack_ludata: bool = True,
unpack_pivots: bool = True,
name: str | None = None
)
tuple[Tensor, Tensor, Tensor]
lu_unpack¶
-
Unpack L U and P to single matrix tensor . unpack L and U matrix from LU, unpack permutation matrix P from Pivots .
P mat can be get by pivots:
ones = eye(rows) #eye matrix of rank rows for i in range(cols): swap(ones[i], ones[pivots[i]])- Parameters
-
x (Tensor) – The LU tensor get from paddle.linalg.lu, which is combined by L and U. Its data type should be float32, float64, complex64, or complex128.
y (Tensor) – Pivots get from paddle.linalg.lu. Its data type should be int32.
unpack_ludata (bool, optional) – whether to unpack L and U from x. Default: True.
unpack_pivots (bool, optional) – whether to unpack permutation matrix P from Pivots. Default: True.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
P (Tensor), Permutation matrix P of lu factorization.
L (Tensor), The lower triangular matrix tensor of lu factorization.
U (Tensor), The upper triangular matrix tensor of lu factorization.
Examples
>>> import paddle >>> x = paddle.to_tensor([[1.0, 2.0], [3.0, 4.0], [5.0, 6.0]]).astype('float64') >>> lu,p,info = paddle.linalg.lu(x, get_infos=True) >>> print(lu) Tensor(shape=[3, 2], dtype=float64, place=Place(cpu), stop_gradient=True, [[5. , 6. ], [0.20000000, 0.80000000], [0.60000000, 0.50000000]]) >>> print(p) Tensor(shape=[2], dtype=int32, place=Place(cpu), stop_gradient=True, [3, 3]) >>> print(info) Tensor(shape=[], dtype=int32, place=Place(cpu), stop_gradient=True, 0) >>> P,L,U = paddle.linalg.lu_unpack(lu,p) >>> print(P) Tensor(shape=[3, 3], dtype=float64, place=Place(cpu), stop_gradient=True, [[0., 1., 0.], [0., 0., 1.], [1., 0., 0.]]) >>> print(L) Tensor(shape=[3, 2], dtype=float64, place=Place(cpu), stop_gradient=True, [[1. , 0. ], [0.20000000, 1. ], [0.60000000, 0.50000000]]) >>> print(U) Tensor(shape=[2, 2], dtype=float64, place=Place(cpu), stop_gradient=True, [[5. , 6. ], [0. , 0.80000000]]) >>> # one can verify : X = P @ L @ U ;
-
masked_fill
(
mask: Tensor,
value: Numeric,
name: str | None = None
)
Tensor
masked_fill¶
-
Fills elements of self tensor with value where mask is True. The shape of mask must be broadcastable with the shape of the underlying tensor.
The following figure shows an example: consider a 3x3 matrix x,where all elements have a value of 1, and a matrix mask of the same size, and value is 3.

- Parameters
-
x (Tensor) – The Destination Tensor. Supported data types are float, double, int, int64_t,float16 and bfloat16.
mask (Tensor) – The boolean tensor indicate the position to be filled. The data type of mask must be bool.
value (Scalar or 0-D Tensor) – The value used to fill the target tensor. Supported data types are float, double, int, int64_t,float16 and bfloat16.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
- Returns
-
Tensor, same dimension and dtype with x.
Examples
>>> >>> import paddle >>> x = paddle.ones((3, 3), dtype="float32") >>> mask = paddle.to_tensor([[True, True, False]]) >>> print(mask) Tensor(shape=[1, 3], dtype=bool, place=Place(gpu:0), stop_gradient=True, [[True , True , False]]) >>> out = paddle.masked_fill(x, mask, 2) >>> print(out) Tensor(shape=[3, 3], dtype=float32, place=Place(gpu:0), stop_gradient=True, [[2., 2., 1.], [2., 2., 1.], [2., 2., 1.]])
-
masked_fill_
(
mask: Tensor,
value: Numeric,
name: str | None = None
)
Tensor
masked_fill_¶
-
Inplace version of
masked_fillAPI, the output Tensor will be inplaced with inputx. Please refer to masked_fill.
-
masked_scatter
(
mask: Tensor,
value: Tensor,
name: str | None = None
)
Tensor
masked_scatter¶
-
Copies elements from value into x tensor at positions where the mask is True.
Elements from source are copied into x starting at position 0 of value and continuing in order one-by-one for each occurrence of mask being True. The shape of mask must be broadcastable with the shape of the underlying tensor. The value should have at least as many elements as the number of ones in mask.
The image illustrates a typical case of the masked_scatter operation.
Tensor
value: Contains the data to be filled into the target tensor. Only the parts where the mask is True will take values from the value tensor, while the rest will be ignored;Tensor
mask: Specifies which positions should extract values from the value tensor and update the target tensor. True indicates the corresponding position needs to be updated;Tensor
origin: The input tensor, where only the parts satisfying the mask will be replaced, and the rest remains unchanged;
Result: After the
masked_scatteroperation, the parts of theorigintensor where themaskisTrueare updated with the corresponding values from thevaluetensor, while the parts where themaskisFalseremain unchanged, forming the final updated tensor.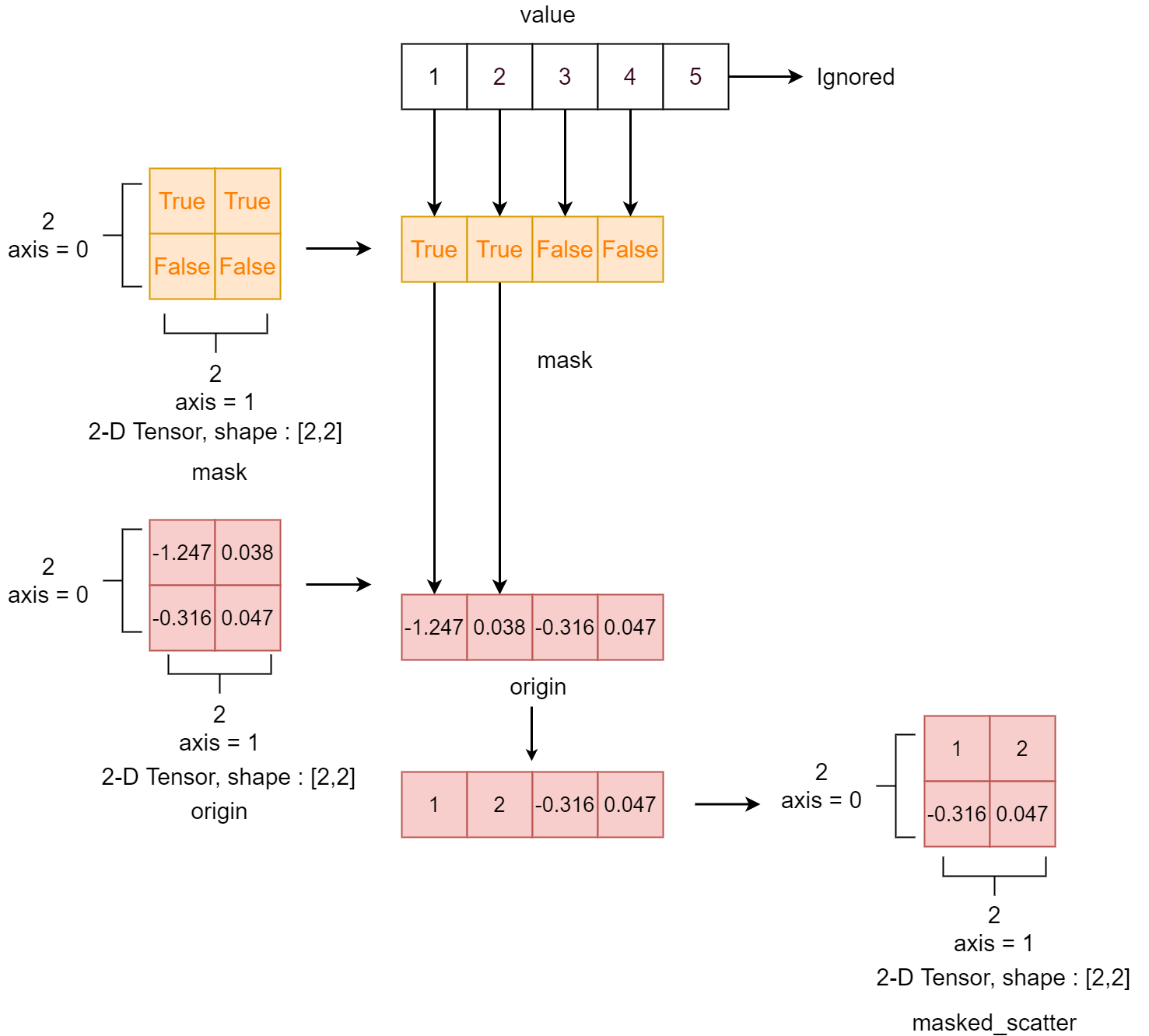
- Parameters
-
x (Tensor) – An N-D Tensor. The data type is
float16,float32,float64,int32,int64orbfloat16.mask (Tensor) – The boolean tensor indicate the position to be filled. The data type of mask must be bool.
value (Tensor) – The value used to fill the target tensor. Supported data types are same as x.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, A reshaped Tensor with the same data type as
x.
Examples
>>> import paddle >>> paddle.seed(2048) >>> x = paddle.randn([2, 2]) >>> print(x) Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True, [[-1.24725831, 0.03843464], [-0.31660911, 0.04793844]]) >>> mask = paddle.to_tensor([[True, True], [False, False]]) >>> value = paddle.to_tensor([1, 2, 3, 4, 5,], dtype="float32") >>> out = paddle.masked_scatter(x, mask, value) >>> print(out) Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True, [[1, 2], [-0.31660911, 0.04793844]])
-
masked_scatter_
(
mask: Tensor,
value: Tensor,
name: str | None = None
)
Tensor
masked_scatter_¶
-
Inplace version of
masked_scatterAPI, the output Tensor will be inplaced with inputx. Please refer to masked_scatter.
-
masked_select
(
mask: Tensor,
name: str | None = None
)
Tensor
masked_select¶
-
Returns a new 1-D tensor which indexes the input tensor according to the
maskwhich is a tensor with data type of bool.Note
paddle.masked_selectsupports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .- Parameters
-
x (Tensor) – The input Tensor, the data type can be int32, int64, uint16, float16, float32, float64.
mask (Tensor) – The Tensor containing the binary mask to index with, it’s data type is bool.
name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Returns
-
Tensor, A 1-D Tensor which is the same data type as
x.
Examples
>>> import paddle >>> x = paddle.to_tensor([[1.0, 2.0, 3.0, 4.0], ... [5.0, 6.0, 7.0, 8.0], ... [9.0, 10.0, 11.0, 12.0]]) >>> mask = paddle.to_tensor([[True, False, False, False], ... [True, True, False, False], ... [True, False, False, False]]) >>> out = paddle.masked_select(x, mask) >>> print(out.numpy()) [1. 5. 6. 9.]
-
matmul
(
)
matmul¶
-
C++ interface function for matmul.
-
matrix_power
(
n: int,
name: str | None = None
)
tuple[Tensor, int]
matrix_power¶
-
Computes the n-th power of a square matrix or a batch of square matrices.
Let \(X\) be a square matrix or a batch of square matrices, \(n\) be an exponent, the equation should be:
\[Out = X ^ {n}\]Specifically,
If n > 0, it returns the matrix or a batch of matrices raised to the power of n.
If n = 0, it returns the identity matrix or a batch of identity matrices.
If n < 0, it returns the inverse of each matrix (if invertible) raised to the power of abs(n).
- Parameters
-
x (Tensor) – A square matrix or a batch of square matrices to be raised to power n. Its shape should be [*, M, M], where * is zero or more batch dimensions. Its data type should be float32 or float64.
n (int) – The exponent. It can be any positive, negative integer or zero.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, The n-th power of the matrix (or the batch of matrices) x. Its data type should be the same as that of x.
Examples
>>> import paddle >>> x = paddle.to_tensor([[1, 2, 3], ... [1, 4, 9], ... [1, 8, 27]], dtype='float64') >>> print(paddle.linalg.matrix_power(x, 2)) Tensor(shape=[3, 3], dtype=float64, place=Place(cpu), stop_gradient=True, [[6. , 34. , 102.], [14. , 90. , 282.], [36. , 250., 804.]]) >>> print(paddle.linalg.matrix_power(x, 0)) Tensor(shape=[3, 3], dtype=float64, place=Place(cpu), stop_gradient=True, [[1., 0., 0.], [0., 1., 0.], [0., 0., 1.]]) >>> print(paddle.linalg.matrix_power(x, -2)) Tensor(shape=[3, 3], dtype=float64, place=Place(cpu), stop_gradient=True, [[ 12.91666667, -12.75000000, 2.83333333 ], [-7.66666667 , 8. , -1.83333333 ], [ 1.80555556 , -1.91666667 , 0.44444444 ]])
-
matrix_transpose
(
name: Optional[str] = None
)
Tensor
matrix_transpose¶
-
Transpose the last two dimensions of the input tensor x.
Note
If n is the number of dimensions of x, paddle.matrix_transpose(x) is equivalent to x.transpose([0, 1, …, n-2, n-1]).
- Parameters
-
x (Tensor) – The input tensor to be transposed. x must be an N-dimensional tensor (N >= 2) of any data type supported by Paddle.
name (str|None, optional) – The name of this layer. For more information, please refer to api_guide_Name. Default is None.
- Returns
-
A new tensor with the same shape as x, except that the last two dimensions are transposed.
- Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.ones(shape=[2, 3, 5]) >>> x_transposed = paddle.matrix_transpose(x) >>> print(x_transposed.shape) [2, 5, 3]
-
max
(
axis: int | Sequence[int] | None = None,
keepdim: bool = False,
name: str | None = None
)
Tensor
max¶
-
Computes the maximum of tensor elements over the given axis.
Note
The difference between max and amax is: If there are multiple maximum elements, amax evenly distributes gradient between these equal values, while max propagates gradient to all of them.
- Parameters
-
x (Tensor) – A tensor, the data type is float8_e4m3fn, float8_e5m2, bfloat16, float16, float32, float64, int32, int64.
axis (int|list|tuple|None, optional) – The axis along which the maximum is computed. If
None, compute the maximum over all elements of x and return a Tensor with a single element, otherwise must be in the range \([-x.ndim(x), x.ndim(x))\). If \(axis[i] < 0\), the axis to reduce is \(x.ndim + axis[i]\).keepdim (bool, optional) – Whether to reserve the reduced dimension in the output Tensor. The result tensor will have one fewer dimension than the x unless
keepdimis true, default value is False.name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, results of maximum on the specified axis of input tensor, it’s data type is the same as x.
Examples
>>> import paddle >>> # data_x is a Tensor with shape [2, 4] >>> # the axis is a int element >>> x = paddle.to_tensor([[0.2, 0.3, 0.5, 0.9], ... [0.1, 0.2, 0.6, 0.7]], ... dtype='float64', stop_gradient=False) >>> result1 = paddle.max(x) >>> result1.backward() >>> result1 Tensor(shape=[], dtype=float64, place=Place(cpu), stop_gradient=False, 0.90000000) >>> x.grad Tensor(shape=[2, 4], dtype=float64, place=Place(cpu), stop_gradient=False, [[0., 0., 0., 1.], [0., 0., 0., 0.]]) >>> x.clear_grad() >>> result2 = paddle.max(x, axis=0) >>> result2.backward() >>> result2 Tensor(shape=[4], dtype=float64, place=Place(cpu), stop_gradient=False, [0.20000000, 0.30000000, 0.60000000, 0.90000000]) >>> x.grad Tensor(shape=[2, 4], dtype=float64, place=Place(cpu), stop_gradient=False, [[1., 1., 0., 1.], [0., 0., 1., 0.]]) >>> x.clear_grad() >>> result3 = paddle.max(x, axis=-1) >>> result3.backward() >>> result3 Tensor(shape=[2], dtype=float64, place=Place(cpu), stop_gradient=False, [0.90000000, 0.70000000]) >>> x.grad Tensor(shape=[2, 4], dtype=float64, place=Place(cpu), stop_gradient=False, [[0., 0., 0., 1.], [0., 0., 0., 1.]]) >>> x.clear_grad() >>> result4 = paddle.max(x, axis=1, keepdim=True) >>> result4.backward() >>> result4 Tensor(shape=[2, 1], dtype=float64, place=Place(cpu), stop_gradient=False, [[0.90000000], [0.70000000]]) >>> x.grad Tensor(shape=[2, 4], dtype=float64, place=Place(cpu), stop_gradient=False, [[0., 0., 0., 1.], [0., 0., 0., 1.]]) >>> # data_y is a Tensor with shape [2, 2, 2] >>> # the axis is list >>> y = paddle.to_tensor([[[1.0, 2.0], [3.0, 4.0]], ... [[5.0, 6.0], [7.0, 8.0]]], ... dtype='float64', stop_gradient=False) >>> result5 = paddle.max(y, axis=[1, 2]) >>> result5.backward() >>> result5 Tensor(shape=[2], dtype=float64, place=Place(cpu), stop_gradient=False, [4., 8.]) >>> y.grad Tensor(shape=[2, 2, 2], dtype=float64, place=Place(cpu), stop_gradient=False, [[[0., 0.], [0., 1.]], [[0., 0.], [0., 1.]]]) >>> y.clear_grad() >>> result6 = paddle.max(y, axis=[0, 1]) >>> result6.backward() >>> result6 Tensor(shape=[2], dtype=float64, place=Place(cpu), stop_gradient=False, [7., 8.]) >>> y.grad Tensor(shape=[2, 2, 2], dtype=float64, place=Place(cpu), stop_gradient=False, [[[0., 0.], [0., 0.]], [[0., 0.], [1., 1.]]])
-
maximum
(
)
maximum¶
-
C++ interface function for maximum.
-
mean
(
axis: int | Sequence[int] | None = None,
keepdim: bool = False,
name: str | None = None,
*,
dtype: DTypeLike | None = None,
out: Tensor | None = None
)
Tensor
mean¶
-
Computes the mean of the input tensor’s elements along
axis.- Parameters
-
x (Tensor) – The input Tensor with data type bool, bfloat16, float16, float32, float64, int32, int64, complex64, complex128. alias:
inputaxis (int|list|tuple|None, optional) – The axis along which to perform mean calculations.
axisshould be int, list(int) or tuple(int). Ifaxisis a list/tuple of dimension(s), mean is calculated along all element(s) ofaxis.axisor element(s) ofaxisshould be in range [-D, D), where D is the dimensions ofx. Ifaxisor element(s) ofaxisis less than 0, it works the same way as \(axis + D\) . Ifaxisis None, mean is calculated over all elements ofx. Default is None. alias:dimkeepdim (bool, optional) – Whether to reserve the reduced dimension(s) in the output Tensor. If
keepdimis True, the dimensions of the output Tensor is the same asxexcept in the reduced dimensions(it is of size 1 in this case). Otherwise, the shape of the output Tensor is squeezed inaxis. Default is False.name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
dtype (str) – The desired data type of returned tensor. Default: None.
out (Tensor|None, optional) – The output tensor. Default: None.
- Returns
-
Tensor, results of average along
axisofx, with the same data type asx.
Examples
>>> import paddle >>> x = paddle.to_tensor([[[1., 2., 3., 4.], ... [5., 6., 7., 8.], ... [9., 10., 11., 12.]], ... [[13., 14., 15., 16.], ... [17., 18., 19., 20.], ... [21., 22., 23., 24.]]]) >>> out1 = paddle.mean(x) >>> print(out1.numpy()) 12.5 >>> out2 = paddle.mean(x, axis=-1) >>> print(out2.numpy()) [[ 2.5 6.5 10.5] [14.5 18.5 22.5]] >>> out3 = paddle.mean(x, axis=-1, keepdim=True) >>> print(out3.numpy()) [[[ 2.5] [ 6.5] [10.5]] [[14.5] [18.5] [22.5]]] >>> out4 = paddle.mean(x, axis=[0, 2]) >>> print(out4.numpy()) [ 8.5 12.5 16.5] >>> out5 = paddle.mean(x, dtype='float64') >>> out5 Tensor(shape=[], dtype=float64, place=Place(gpu:0), stop_gradient=True, 12.50000000)
-
median
(
axis=None,
keepdim=False,
mode='avg',
name=None
)
median¶
-
Compute the median along the specified axis.
Note
Alias Support: The parameter name
inputcan be used as an alias forx, anddimcan be used as an alias foraxis. When an alias replacement occurs, the default parameter for mode setting is min instead of avg. For example,median(input=tensor_x, dim=1, ...)is equivalent tomedian(x=tensor_x, axis=1, ...).- Parameters
-
x (Tensor) – The input Tensor, it’s data type can be bfloat16, float16, float32, float64, int32, int64. alias:
input.axis (int|None, optional) – The axis along which to perform median calculations
axisshould be int. alias:dim.axisshould be in range [-D, D), where D is the dimensions ofx. Ifaxisis less than 0, it works the same way as \(axis + D\). Ifaxisis None, median is calculated over all elements ofx. Default is None.keepdim (bool, optional) – Whether to reserve the reduced dimension(s) in the output Tensor. If
keepdimis True, the dimensions of the output Tensor is the same asxexcept in the reduced dimensions(it is of size 1 in this case). Otherwise, the shape of the output Tensor is squeezed inaxis. Default is False.mode (str, optional) – Whether to use mean or min operation to calculate the median values when the input tensor has an even number of elements in the dimension
axis. Support ‘avg’ and ‘min’. Default is ‘avg’. When an alias replacement occurs, the default parameter for mode setting is min instead of avg.name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor or tuple of Tensor. If
mode== ‘avg’, the result will be the tensor of median values; Ifmode== ‘min’ andaxisis None, the result will be the tensor of median values; Ifmode== ‘min’ andaxisis not None, the result will be a tuple of two tensors containing median values and their indices.When
mode== ‘avg’, if data type ofxis float64, data type of median values will be float64, otherwise data type of median values will be float32. Whenmode== ‘min’, the data type of median values will be the same asx. The data type of indices will be int64.
Examples
>>> import paddle >>> import numpy as np >>> x = paddle.arange(12).reshape([3, 4]) >>> print(x) Tensor(shape=[3, 4], dtype=int64, place=Place(cpu), stop_gradient=True, [[0 , 1 , 2 , 3 ], [4 , 5 , 6 , 7 ], [8 , 9 , 10, 11]]) >>> y1 = paddle.median(x) >>> print(y1) Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 5.50000000) >>> y2 = paddle.median(x, axis=0) >>> print(y2) Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [4., 5., 6., 7.]) >>> y3 = paddle.median(x, axis=1) >>> print(y3) Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True, [1.50000000, 5.50000000, 9.50000000]) >>> y4 = paddle.median(x, axis=0, keepdim=True) >>> print(y4) Tensor(shape=[1, 4], dtype=float32, place=Place(cpu), stop_gradient=True, [[4., 5., 6., 7.]]) >>> y5 = paddle.median(x, mode='min') >>> print(y5) Tensor(shape=[], dtype=int64, place=Place(cpu), stop_gradient=True, 5) >>> median_value, median_indices = paddle.median(x, axis=1, mode='min') >>> print(median_value) Tensor(shape=[3], dtype=int64, place=Place(cpu), stop_gradient=True, [1, 5, 9]) >>> print(median_indices) Tensor(shape=[3], dtype=int64, place=Place(cpu), stop_gradient=True, [1, 1, 1]) >>> # cases containing nan values >>> x = paddle.to_tensor(np.array([[1,float('nan'),3,float('nan')],[1,2,3,4],[float('nan'),1,2,3]])) >>> y6 = paddle.median(x, axis=-1, keepdim=True) >>> print(y6) Tensor(shape=[3, 1], dtype=float64, place=Place(cpu), stop_gradient=True, [[nan ], [2.50000000], [nan ]]) >>> median_value, median_indices = paddle.median(x, axis=1, keepdim=True, mode='min') >>> print(median_value) Tensor(shape=[3, 1], dtype=float64, place=Place(cpu), stop_gradient=True, [[nan], [2. ], [nan]]) >>> print(median_indices) Tensor(shape=[3, 1], dtype=int64, place=Place(cpu), stop_gradient=True, [[1], [1], [0]])
-
min
(
axis: int | Sequence[int] | None = None,
keepdim: bool = False,
name: str | None = None
)
Tensor
min¶
-
Computes the minimum of tensor elements over the given axis
Note
The difference between min and amin is: If there are multiple minimum elements, amin evenly distributes gradient between these equal values, while min propagates gradient to all of them.
- Parameters
-
x (Tensor) – A tensor, the data type is bfloat16, float16, float32, float64, int32, int64.
axis (int|list|tuple|None, optional) – The axis along which the minimum is computed. If
None, compute the minimum over all elements of x and return a Tensor with a single element, otherwise must be in the range \([-x.ndim, x.ndim)\). If \(axis[i] < 0\), the axis to reduce is \(x.ndim + axis[i]\).keepdim (bool, optional) – Whether to reserve the reduced dimension in the output Tensor. The result tensor will have one fewer dimension than the x unless
keepdimis true, default value is False.name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, results of minimum on the specified axis of input tensor, it’s data type is the same as input’s Tensor.
Examples
>>> import paddle >>> # data_x is a Tensor with shape [2, 4] >>> # the axis is a int element >>> x = paddle.to_tensor([[0.2, 0.3, 0.5, 0.9], ... [0.1, 0.2, 0.6, 0.7]], ... dtype='float64', stop_gradient=False) >>> result1 = paddle.min(x) >>> result1.backward() >>> result1 Tensor(shape=[], dtype=float64, place=Place(cpu), stop_gradient=False, 0.10000000) >>> x.grad Tensor(shape=[2, 4], dtype=float64, place=Place(cpu), stop_gradient=False, [[0., 0., 0., 0.], [1., 0., 0., 0.]]) >>> x.clear_grad() >>> result2 = paddle.min(x, axis=0) >>> result2.backward() >>> result2 Tensor(shape=[4], dtype=float64, place=Place(cpu), stop_gradient=False, [0.10000000, 0.20000000, 0.50000000, 0.70000000]) >>> x.grad Tensor(shape=[2, 4], dtype=float64, place=Place(cpu), stop_gradient=False, [[0., 0., 1., 0.], [1., 1., 0., 1.]]) >>> x.clear_grad() >>> result3 = paddle.min(x, axis=-1) >>> result3.backward() >>> result3 Tensor(shape=[2], dtype=float64, place=Place(cpu), stop_gradient=False, [0.20000000, 0.10000000]) >>> x.grad Tensor(shape=[2, 4], dtype=float64, place=Place(cpu), stop_gradient=False, [[1., 0., 0., 0.], [1., 0., 0., 0.]]) >>> x.clear_grad() >>> result4 = paddle.min(x, axis=1, keepdim=True) >>> result4.backward() >>> result4 Tensor(shape=[2, 1], dtype=float64, place=Place(cpu), stop_gradient=False, [[0.20000000], [0.10000000]]) >>> x.grad Tensor(shape=[2, 4], dtype=float64, place=Place(cpu), stop_gradient=False, [[1., 0., 0., 0.], [1., 0., 0., 0.]]) >>> # data_y is a Tensor with shape [2, 2, 2] >>> # the axis is list >>> y = paddle.to_tensor([[[1.0, 2.0], [3.0, 4.0]], ... [[5.0, 6.0], [7.0, 8.0]]], ... dtype='float64', stop_gradient=False) >>> result5 = paddle.min(y, axis=[1, 2]) >>> result5.backward() >>> result5 Tensor(shape=[2], dtype=float64, place=Place(cpu), stop_gradient=False, [1., 5.]) >>> y.grad Tensor(shape=[2, 2, 2], dtype=float64, place=Place(cpu), stop_gradient=False, [[[1., 0.], [0., 0.]], [[1., 0.], [0., 0.]]]) >>> y.clear_grad() >>> result6 = paddle.min(y, axis=[0, 1]) >>> result6.backward() >>> result6 Tensor(shape=[2], dtype=float64, place=Place(cpu), stop_gradient=False, [1., 2.]) >>> y.grad Tensor(shape=[2, 2, 2], dtype=float64, place=Place(cpu), stop_gradient=False, [[[1., 1.], [0., 0.]], [[0., 0.], [0., 0.]]])
-
minimum
(
)
minimum¶
-
C++ interface function for minimum.
-
mm
(
mat2: Tensor,
name: str | None = None
)
Tensor
mm¶
-
Applies matrix multiplication to two tensors.
Currently, the input tensors’ rank can be any, but when the rank of any inputs is bigger than 3, this two inputs’ rank should be equal.
Also note that if the raw tensor \(x\) or \(mat2\) is rank-1 and nontransposed, the prepended or appended dimension \(1\) will be removed after matrix multiplication.
- Parameters
-
input (Tensor) – The input tensor which is a Tensor. Support data types: bfloat16, float16, float32, float64, int8, int32, int64, complex64, complex128.
mat2 (Tensor) – The input tensor which is a Tensor. Support data types: bfloat16, float16, float32, float64, int8, int32, int64, complex64, complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
The product Tensor, with same data type of the input Tensor.
- Return type
-
Tensor
* example 1: input: [B, ..., M, K], mat2: [B, ..., K, N] out: [B, ..., M, N] * example 2: input: [B, M, K], mat2: [B, K, N] out: [B, M, N] * example 3: input: [B, M, K], mat2: [K, N] out: [B, M, N] * example 4: input: [M, K], mat2: [K, N] out: [M, N] * example 5: input: [B, M, K], mat2: [K] out: [B, M] * example 6: input: [K], mat2: [K] out: [1]
Examples
>>> import paddle >>> input = paddle.arange(1, 7).reshape((3, 2)).astype('float32') >>> mat2 = paddle.arange(1, 9).reshape((2, 4)).astype('float32') >>> out = paddle.mm(input, mat2) >>> out Tensor(shape=[3, 4], dtype=float32, place=Place(cpu), stop_gradient=True, [[11., 14., 17., 20.], [23., 30., 37., 44.], [35., 46., 57., 68.]])
-
mod
(
y: Tensor,
name: str | None = None
)
Tensor
mod¶
-
Mod two tensors element-wise. The equation is:
\[out = x \% y\]Note
paddle.remaindersupports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .And mod, floor_mod are all functions with the same name
- Parameters
-
x (Tensor) – the input tensor, it’s data type should be bfloat16, float16, float32, float64, int32, int64.
y (Tensor) – the input tensor, it’s data type should be bfloat16, float16, float32, float64, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
N-D Tensor. A location into which the result is stored. If x, y have different shapes and are “broadcastable”, the resulting tensor shape is the shape of x and y after broadcasting. If x, y have the same shape, its shape is the same as x and y.
Examples
>>> import paddle >>> x = paddle.to_tensor([2, 3, 8, 7]) >>> y = paddle.to_tensor([1, 5, 3, 3]) >>> z = paddle.remainder(x, y) >>> print(z) Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True, [0, 3, 2, 1]) >>> z = paddle.floor_mod(x, y) >>> print(z) Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True, [0, 3, 2, 1]) >>> z = paddle.mod(x, y) >>> print(z) Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True, [0, 3, 2, 1])
-
mod_
(
y: Tensor,
name: str | None = None
)
Tensor
mod_¶
-
Inplace version of
floor_mod_API, the output Tensor will be inplaced with inputx. Please refer to floor_mod_.
-
mode
(
axis: int = -1,
keepdim: bool = False,
name: str | None = None
)
tuple[Tensor, Tensor]
mode¶
-
Used to find values and indices of the modes at the optional axis.
- Parameters
-
x (Tensor) – Tensor, an input N-D Tensor with type float32, float64, int32, int64.
axis (int, optional) – Axis to compute indices along. The effective range is [-R, R), where R is x.ndim. when axis < 0, it works the same way as axis + R. Default is -1.
keepdim (bool, optional) – Whether to keep the given axis in output. If it is True, the dimensions will be same as input x and with size one in the axis. Otherwise the output dimensions is one fewer than x since the axis is squeezed. Default is False.
name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Returns
-
tuple (Tensor), return the values and indices. The value data type is the same as the input x. The indices data type is int64.
Examples
>>> import paddle >>> tensor = paddle.to_tensor([[[1,2,2],[2,3,3]],[[0,5,5],[9,9,0]]], dtype=paddle.float32) >>> res = paddle.mode(tensor, 2) >>> print(res) (Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True, [[2., 3.], [5., 9.]]), Tensor(shape=[2, 2], dtype=int64, place=Place(cpu), stop_gradient=True, [[2, 2], [2, 1]]))
-
moveaxis
(
source: int | Sequence[int],
destination: int | Sequence[int],
name: str | None = None
)
Tensor
moveaxis¶
-
Move the axis of tensor from
sourceposition todestinationposition.Other axis that have not been moved remain their original order.
- Parameters
-
x (Tensor) – The input Tensor. It is a N-D Tensor of data types bool, int32, int64, float32, float64, complex64, complex128.
source (int|tuple|list) –
sourceposition of axis that will be moved. Each element must be unique and integer.destination (int|tuple|list) –
destinationposition of axis that has been moved. Each element must be unique and integer.name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
- Returns
-
Tensor, A new tensor whose axis have been moved.
Examples
>>> import paddle >>> x = paddle.ones([3, 2, 4]) >>> outshape = paddle.moveaxis(x, [0, 1], [1, 2]).shape >>> print(outshape) [4, 3, 2] >>> x = paddle.ones([2, 3]) >>> outshape = paddle.moveaxis(x, 0, 1).shape # equivalent to paddle.t(x) >>> print(outshape) [3, 2]
-
msort
(
*,
out: Tensor | None = None
)
Tensor
msort¶
-
Sorts the input along the given axis = 0, and returns the sorted output tensor. The sort algorithm is ascending.
- Parameters
-
input (Tensor) – An input N-D Tensor with type float32, float64, int16, int32, int64, uint8.
out (Tensor, optional) – The output tensor.
- Returns
-
Tensor, sorted tensor(with the same shape and data type as
input).
Examples
>>> import paddle >>> x = paddle.to_tensor([[[5,8,9,5], ... [0,0,1,7], ... [6,9,2,4]], ... [[5,2,4,2], ... [4,7,7,9], ... [1,7,0,6]]], ... dtype='float32') >>> out1 = paddle.msort(input=x) >>> print(out1.numpy()) [[[5. 2. 4. 2.] [0. 0. 1. 7.] [1. 7. 0. 4.]] [[5. 8. 9. 5.] [4. 7. 7. 9.] [6. 9. 2. 6.]]] >>> out2 = paddle.empty_like(x) >>> paddle.msort(input=x, out=out2) >>> print(out2.numpy()) [[[5. 2. 4. 2.] [0. 0. 1. 7.] [1. 7. 0. 4.]] [[5. 8. 9. 5.] [4. 7. 7. 9.] [6. 9. 2. 6.]]]
-
mul
(
y: Tensor,
name: str | None = None,
*,
out: Tensor | None = None
)
Tensor
mul¶
-
multiply two tensors element-wise. The equation is:
\[out = x * y\]Note
Supported shape of
xandyfor this operator: 1. x.shape == y.shape. 2. x.shape could be the continuous subsequence of y.shape.paddle.mulsupports broadcasting. If you would like to know more about broadcasting, please refer to Introduction to Tensor .- Parameters
-
x (Tensor) – the input tensor, its data type should be one of bfloat16, float16, float32, float64, int32, int64, bool, complex64, complex128.
y (Tensor) – the input tensor, its data type should be one of bfloat16, float16, float32, float64, int32, int64, bool, complex64, complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
out (Tensor|None, optional) – The output tensor. If set, the result will be stored in this tensor. Default is None.
- Returns
-
N-D Tensor. A location into which the result is stored. If
x,yhave different shapes and are “broadcastable”, the resulting tensor shape is the shape ofxandyafter broadcasting. Ifx,yhave the same shape, its shape is the same asxandy.
Examples
>>> import paddle >>> x = paddle.to_tensor([[1, 2], [3, 4]]) >>> y = paddle.to_tensor([[5, 6], [7, 8]]) >>> res = paddle.mul(x, y) >>> print(res) Tensor(shape=[2, 2], dtype=int64, place=Place(cpu), stop_gradient=True, [[5 , 12], [21, 32]]) >>> x = paddle.to_tensor([[[1, 2, 3], [1, 2, 3]]]) >>> y = paddle.to_tensor([2]) >>> res = paddle.mul(x, y) >>> print(res) Tensor(shape=[1, 2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[[2, 4, 6], [2, 4, 6]]])
-
mul_
(
y: Tensor,
name: str | None = None
)
Tensor
mul_¶
-
Inplace version of
multiplyAPI, the output Tensor will be inplaced with inputx. Please refer to multiply.
-
multi_dot
(
name: str | None = None
)
Tensor
multi_dot¶
-
Multi_dot is an operator that calculates multiple matrix multiplications.
Supports inputs of float16(only GPU support), float32 and float64 dtypes. This function does not support batched inputs.
The input tensor in [x] must be 2-D except for the first and last can be 1-D. If the first tensor is a 1-D vector of shape(n, ) it is treated as row vector of shape(1, n), similarly if the last tensor is a 1D vector of shape(n, ), it is treated as a column vector of shape(n, 1).
If the first and last tensor are 2-D matrix, then the output is also 2-D matrix, otherwise the output is a 1-D vector.
Multi_dot will select the lowest cost multiplication order for calculation. The cost of multiplying two matrices with shapes (a, b) and (b, c) is a * b * c. Given matrices A, B, C with shapes (20, 5), (5, 100), (100, 10) respectively, we can calculate the cost of different multiplication orders as follows: - Cost((AB)C) = 20x5x100 + 20x100x10 = 30000 - Cost(A(BC)) = 5x100x10 + 20x5x10 = 6000
In this case, multiplying B and C first, then multiply A, which is 5 times faster than sequential calculation.
- Parameters
-
x (list[Tensor]) – The input tensors which is a list Tensor.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
The output Tensor.
- Return type
-
Tensor
Examples
>>> import paddle >>> # A * B >>> A = paddle.rand([3, 4]) >>> B = paddle.rand([4, 5]) >>> out = paddle.linalg.multi_dot([A, B]) >>> print(out.shape) [3, 5] >>> # A * B * C >>> A = paddle.rand([10, 5]) >>> B = paddle.rand([5, 8]) >>> C = paddle.rand([8, 7]) >>> out = paddle.linalg.multi_dot([A, B, C]) >>> print(out.shape) [10, 7]
-
multigammaln
(
p: int,
name: str | None = None
)
Tensor
multigammaln¶
-
This function computes the log of multivariate gamma, also sometimes called the generalized gamma.
- Parameters
-
x (Tensor) – Input Tensor. Must be one of the following types: float16, float32, float64, uint16.
p (int) – The dimension of the space of integration.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
The values of the log multivariate gamma at the given tensor x.
- Return type
-
out (Tensor)
Examples
>>> import paddle >>> x = paddle.to_tensor([2.5, 3.5, 4, 6.5, 7.8, 10.23, 34.25]) >>> p = 2 >>> out = paddle.multigammaln(x, p) >>> print(out) Tensor(shape=[7], dtype=float32, place=Place(cpu), stop_gradient=True, [0.85704780 , 2.46648574 , 3.56509781 , 11.02241898 , 15.84497833 , 26.09257698 , 170.68318176])
-
multigammaln_
(
p: int,
name: str | None = None
)
Tensor
multigammaln_¶
-
Inplace version of
multigammaln_API, the output Tensor will be inplaced with inputx. Please refer to multigammaln.
-
multinomial
(
num_samples: int = 1,
replacement: bool = False,
name: str | None = None,
*,
out: Tensor | None = None
)
Tensor
multinomial¶
-
Returns a Tensor filled with random values sampled from a Multinomial distribution. The input
xis a tensor with probabilities for generating the random number. Each element inxshould be larger or equal to 0, but not all 0.replacementindicates whether it is a replaceable sample. Ifreplacementis True, a category can be sampled more than once.Note
Alias Support: The parameter name
inputcan be used as an alias forx. For example,multinomial(input=tensor_x, ...)is equivalent tomultinomial(x=tensor_x, ...).- Parameters
-
x (Tensor) – A tensor with probabilities for generating the random number. The data type should be float32, float64. alias:
input.num_samples (int, optional) – Number of samples, default is 1.
replacement (bool, optional) – Whether it is a replaceable sample, default is False.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
out (Tensor|None, optional) – The output Tensor. If set, the result will be stored in this Tensor. Default is None.
- Returns
-
Tensor, A Tensor filled with sampled category index after
num_samplestimes samples.
Examples
>>> import paddle >>> paddle.seed(100) # on CPU device >>> x = paddle.rand([2,4]) >>> print(x) >>> Tensor(shape=[2, 4], dtype=float32, place=Place(cpu), stop_gradient=True, [[0.55355281, 0.20714243, 0.01162981, 0.51577556], [0.36369765, 0.26091650, 0.18905126, 0.56219709]]) >>> >>> paddle.seed(200) # on CPU device >>> out1 = paddle.multinomial(x, num_samples=5, replacement=True) >>> print(out1) >>> Tensor(shape=[2, 5], dtype=int64, place=Place(cpu), stop_gradient=True, [[3, 3, 0, 0, 0], [3, 3, 3, 1, 0]]) >>> >>> # out2 = paddle.multinomial(x, num_samples=5) >>> # InvalidArgumentError: When replacement is False, number of samples >>> # should be less than non-zero categories >>> paddle.seed(300) # on CPU device >>> out3 = paddle.multinomial(x, num_samples=3) >>> print(out3) >>> Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[3, 0, 1], [3, 1, 0]]) >>>
-
multiplex
(
index: Tensor,
name: str | None = None
)
Tensor
multiplex¶
-
Based on the given index parameter, the OP selects a specific row from each input Tensor to construct the output Tensor.
If the input of this OP contains \(m\) Tensors, where \(I_{i}\) means the i-th input Tensor, \(i\) between \([0,m)\) .
And \(O\) means the output, where \(O[i]\) means the i-th row of the output, then the output satisfies that \(O[i] = I_{index[i]}[i]\) .
For Example:
Given: inputs = [[[0,0,3,4], [0,1,3,4], [0,2,4,4], [0,3,3,4]], [[1,0,3,4], [1,1,7,8], [1,2,4,2], [1,3,3,4]], [[2,0,3,4], [2,1,7,8], [2,2,4,2], [2,3,3,4]], [[3,0,3,4], [3,1,7,8], [3,2,4,2], [3,3,3,4]]] index = [[3],[0],[1],[2]] out = [[3,0,3,4], # out[0] = inputs[index[0]][0] = inputs[3][0] = [3,0,3,4] [0,1,3,4], # out[1] = inputs[index[1]][1] = inputs[0][1] = [0,1,3,4] [1,2,4,2], # out[2] = inputs[index[2]][2] = inputs[1][2] = [1,2,4,2] [2,3,3,4]] # out[3] = inputs[index[3]][3] = inputs[2][3] = [2,3,3,4]- Parameters
-
inputs (list[Tensor]|tuple[Tensor, ...]) – The input Tensor list. The list elements are N-D Tensors of data types float32, float64, int32, int64, complex64, complex128. All input Tensor shapes should be the same and rank must be at least 2.
index (Tensor) – Used to select some rows in the input Tensor to construct an index of the output Tensor. It is a 2-D Tensor with data type int32 or int64 and shape [M, 1], where M is the number of input Tensors.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Output of multiplex OP, with data type being float32, float64, int32, int64.
- Return type
-
Tensor
Examples
>>> import paddle >>> img1 = paddle.to_tensor([[1, 2], [3, 4]], dtype=paddle.float32) >>> img2 = paddle.to_tensor([[5, 6], [7, 8]], dtype=paddle.float32) >>> inputs = [img1, img2] >>> index = paddle.to_tensor([[1], [0]], dtype=paddle.int32) >>> res = paddle.multiplex(inputs, index) >>> print(res) Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True, [[5., 6.], [3., 4.]])
-
multiply
(
)
multiply¶
-
C++ interface function for multiply.
-
multiply_
(
y: Tensor,
name: str | None = None
)
Tensor
multiply_¶
-
Inplace version of
multiplyAPI, the output Tensor will be inplaced with inputx. Please refer to multiply.
-
mv
(
vec: Tensor,
name: str | None = None
)
Tensor
mv¶
-
Performs a matrix-vector product of the matrix x and the vector vec.
- Parameters
-
x (Tensor) – A tensor with shape \([M, N]\) , The data type of the input Tensor x should be one of float32, float64.
vec (Tensor) – A tensor with shape \([N]\) , The data type of the input Tensor x should be one of float32, float64.
name (str|None, optional) – Normally there is no need for user to set this property. For more information, please refer to api_guide_Name. Default is None.
- Returns
-
The tensor which is produced by x and vec.
- Return type
-
Tensor
Examples
>>> # x: [M, N], vec: [N] >>> # paddle.mv(x, vec) # out: [M] >>> import paddle >>> x = paddle.to_tensor([[2, 1, 3], [3, 0, 1]]).astype("float64") >>> vec = paddle.to_tensor([3, 5, 1]).astype("float64") >>> out = paddle.mv(x, vec) >>> print(out) Tensor(shape=[2], dtype=float64, place=Place(cpu), stop_gradient=True, [14., 10.])
-
nan_to_num
(
nan: float = 0.0,
posinf: float | None = None,
neginf: float | None = None,
name: str | None = None
)
Tensor
nan_to_num¶
-
Replaces NaN, positive infinity, and negative infinity values in input tensor.
- Parameters
-
x (Tensor) – An N-D Tensor, the data type is float32, float64.
nan (float, optional) – the value to replace NaNs with. Default is 0.
posinf (float|None, optional) – if a Number, the value to replace positive infinity values with. If None, positive infinity values are replaced with the greatest finite value representable by input’s dtype. Default is None.
neginf (float|None, optional) – if a Number, the value to replace negative infinity values with. If None, negative infinity values are replaced with the lowest finite value representable by input’s dtype. Default is None.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Results of nan_to_num operation input Tensor
x. - Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.to_tensor([float('nan'), 0.3, float('+inf'), float('-inf')], dtype='float32') >>> out1 = paddle.nan_to_num(x) >>> out1 Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [ 0. , 0.30000001 , 340282346638528859811704183484516925440., -340282346638528859811704183484516925440.]) >>> out2 = paddle.nan_to_num(x, nan=1) >>> out2 Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [ 1. , 0.30000001 , 340282346638528859811704183484516925440., -340282346638528859811704183484516925440.]) >>> out3 = paddle.nan_to_num(x, posinf=5) >>> out3 Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [ 0. , 0.30000001 , 5. , -340282346638528859811704183484516925440.]) >>> out4 = paddle.nan_to_num(x, nan=10, neginf=-99) >>> out4 Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [ 10. , 0.30000001 , 340282346638528859811704183484516925440., -99. ])
-
nan_to_num_
(
nan: float = 0.0,
posinf: float | None = None,
neginf: float | None = None,
name: str | None = None
)
Tensor
nan_to_num_¶
-
Inplace version of
nan_to_numAPI, the output Tensor will be inplaced with inputx. Please refer to nan_to_num.
-
nanmean
(
axis: int | Sequence[int] | None = None,
keepdim: bool = False,
name: str | None = None
)
Tensor
nanmean¶
-
Compute the arithmetic mean along the specified axis, ignoring NaNs.
- Parameters
-
x (Tensor) – The input Tensor with data type uint16, float16, float32, float64.
axis (int|list|tuple, optional) – The axis along which to perform nanmean calculations.
axisshould be int, list(int) or tuple(int). Ifaxisis a list/tuple of dimension(s), nanmean is calculated along all element(s) ofaxis.axisor element(s) ofaxisshould be in range [-D, D), where D is the dimensions ofx. Ifaxisor element(s) ofaxisis less than 0, it works the same way as \(axis + D\) . Ifaxisis None, nanmean is calculated over all elements ofx. Default is None.keepdim (bool, optional) – Whether to reserve the reduced dimension(s) in the output Tensor. If
keepdimis True, the dimensions of the output Tensor is the same asxexcept in the reduced dimensions(it is of size 1 in this case). Otherwise, the shape of the output Tensor is squeezed inaxis. Default is False.name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, results of arithmetic mean along
axisofx, with the same data type asx.
Examples
>>> import paddle >>> # x is a 2-D Tensor: >>> x = paddle.to_tensor([[float('nan'), 0.3, 0.5, 0.9], ... [0.1, 0.2, float('-nan'), 0.7]]) >>> out1 = paddle.nanmean(x) >>> out1 Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 0.44999996) >>> out2 = paddle.nanmean(x, axis=0) >>> out2 Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [0.10000000, 0.25000000, 0.50000000, 0.79999995]) >>> out3 = paddle.nanmean(x, axis=0, keepdim=True) >>> out3 Tensor(shape=[1, 4], dtype=float32, place=Place(cpu), stop_gradient=True, [[0.10000000, 0.25000000, 0.50000000, 0.79999995]]) >>> out4 = paddle.nanmean(x, axis=1) >>> out4 Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True, [0.56666666, 0.33333334]) >>> out5 = paddle.nanmean(x, axis=1, keepdim=True) >>> out5 Tensor(shape=[2, 1], dtype=float32, place=Place(cpu), stop_gradient=True, [[0.56666666], [0.33333334]]) >>> # y is a 3-D Tensor: >>> y = paddle.to_tensor([[[1, float('nan')], [3, 4]], ... [[5, 6], [float('-nan'), 8]]]) >>> out6 = paddle.nanmean(y, axis=[1, 2]) >>> out6 Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True, [2.66666675, 6.33333349]) >>> out7 = paddle.nanmean(y, axis=[0, 1]) >>> out7 Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True, [3., 6.])
-
nanmedian
(
axis=None,
keepdim=False,
mode='avg',
name=None
)
nanmedian¶
-
Compute the median along the specified axis, while ignoring NaNs.
If the valid count of elements is a even number, the average value of both elements in the middle is calculated as the median.
- Parameters
-
x (Tensor) – The input Tensor, it’s data type can be int32, int64, float16, bfloat16, float32, float64.
axis (None|int|list|tuple, optional) – The axis along which to perform median calculations
axisshould be int or list of int.axisshould be in range [-D, D), where D is the dimensions ofx. Ifaxisis less than 0, it works the same way as \(axis + D\). Ifaxisis None, median is calculated over all elements ofx. Default is None.keepdim (bool, optional) – Whether to reserve the reduced dimension(s) in the output Tensor. If
keepdimis True, the dimensions of the output Tensor is the same asxexcept in the reduced dimensions(it is of size 1 in this case). Otherwise, the shape of the output Tensor is squeezed inaxis. Default is False.mode (str, optional) – Whether to use mean or min operation to calculate the nanmedian values when the input tensor has an even number of non-NaN elements along the dimension
axis. Support ‘avg’ and ‘min’. Default is ‘avg’.name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor or tuple of Tensor. If
mode== ‘min’ andaxisis int, the result will be a tuple of two tensors (nanmedian value and nanmedian index). Otherwise, only nanmedian value will be returned.
Examples
>>> import paddle >>> x = paddle.to_tensor([[float('nan'), 2. , 3. ], [0. , 1. , 2. ]]) >>> y1 = x.nanmedian() >>> print(y1.numpy()) 2.0 >>> y2 = x.nanmedian(0) >>> print(y2.numpy()) [0. 1.5 2.5] >>> y3 = x.nanmedian(0, keepdim=True) >>> print(y3.numpy()) [[0. 1.5 2.5]] >>> y4 = x.nanmedian((0, 1)) >>> print(y4.numpy()) 2.0 >>> y5 = x.nanmedian(mode='min') >>> print(y5.numpy()) 2.0 >>> y6, y6_index = x.nanmedian(0, mode='min') >>> print(y6.numpy()) [0. 1. 2.] >>> print(y6_index.numpy()) [1 1 1] >>> y7, y7_index = x.nanmedian(1, mode='min') >>> print(y7.numpy()) [2. 1.] >>> print(y7_index.numpy()) [1 1] >>> y8 = x.nanmedian((0,1), mode='min') >>> print(y8.numpy()) 2.0
-
nanquantile
(
q: float | Sequence[float] | Tensor,
axis: list[int] | int | None = None,
keepdim: bool = False,
interpolation: _Interpolation = 'linear'
)
Tensor
nanquantile¶
-
Compute the quantile of the input as if NaN values in input did not exist. If all values in a reduced row are NaN, then the quantiles for that reduction will be NaN.
- Parameters
-
x (Tensor) – The input Tensor, it’s data type can be float32, float64, int32, int64.
q (int|float|list|Tensor) – The q for calculate quantile, which should be in range [0, 1]. If q is a list or a 1-D Tensor, each element of q will be calculated and the first dimension of output is same to the number of
q. If q is a 0-D Tensor, it will be treated as an integer or float.axis (int|list, optional) – The axis along which to calculate quantile.
axisshould be int or list of int.axisshould be in range [-D, D), where D is the dimensions ofx. Ifaxisis less than 0, it works the same way as \(axis + D\). Ifaxisis a list, quantile is calculated over all elements of given axes. Ifaxisis None, quantile is calculated over all elements ofx. Default is None.keepdim (bool, optional) – Whether to reserve the reduced dimension(s) in the output Tensor. If
keepdimis True, the dimensions of the output Tensor is the same asxexcept in the reduced dimensions(it is of size 1 in this case). Otherwise, the shape of the output Tensor is squeezed inaxis. Default is False.interpolation (str, optional) – The interpolation method to use when the desired quantile falls between two data points. Must be one of linear, higher, lower, midpoint and nearest. Default is linear.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, results of quantile along
axisofx.
Examples
>>> import paddle >>> x = paddle.to_tensor( ... [[0, 1, 2, 3, 4], ... [5, 6, 7, 8, 9]], ... dtype="float32") >>> x[0,0] = float("nan") >>> y1 = paddle.nanquantile(x, q=0.5, axis=[0, 1]) >>> print(y1) Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 5.) >>> y2 = paddle.nanquantile(x, q=0.5, axis=1) >>> print(y2) Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True, [2.50000000, 7. ]) >>> y3 = paddle.nanquantile(x, q=[0.3, 0.5], axis=0) >>> print(y3) Tensor(shape=[2, 5], dtype=float32, place=Place(cpu), stop_gradient=True, [[5. , 2.50000000, 3.50000000, 4.50000000, 5.50000000], [5. , 3.50000000, 4.50000000, 5.50000000, 6.50000000]]) >>> y4 = paddle.nanquantile(x, q=0.8, axis=1, keepdim=True) >>> print(y4) Tensor(shape=[2, 1], dtype=float32, place=Place(cpu), stop_gradient=True, [[3.40000000], [8.20000000]]) >>> nan = paddle.full(shape=[2, 3], fill_value=float("nan")) >>> y5 = paddle.nanquantile(nan, q=0.8, axis=1, keepdim=True) >>> print(y5) Tensor(shape=[2, 1], dtype=float32, place=Place(cpu), stop_gradient=True, [[nan], [nan]])
-
nansum
(
axis: int | Sequence[int] | None = None,
dtype: DTypeLike | None = None,
keepdim: bool = False,
name: str | None = None
)
Tensor
nansum¶
-
Computes the sum of tensor elements over the given axis, treating Not a Numbers (NaNs) as zero.
- Parameters
-
x (Tensor) – An N-D Tensor, the data type is bfloat16, float16, float32, float64, int32 or int64.
axis (int|list|tuple, optional) – The dimensions along which the nansum is performed. If
None, nansum all elements ofxand return a Tensor with a single element, otherwise must be in the range \([-rank(x), rank(x))\). If \(axis[i] < 0\), the dimension to reduce is \(rank + axis[i]\).dtype (str|paddle.dtype|np.dtype, optional) – The dtype of output Tensor. The default value is None, the dtype of output is the same as input Tensor x.
keepdim (bool, optional) – Whether to reserve the reduced dimension in the output Tensor. The result Tensor will have one fewer dimension than the
xunlesskeepdimis true, default value is False.name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Results of summation operation on the specified axis of input Tensor x,
- Return type
-
Tensor
Examples
>>> import paddle >>> # x is a Tensor with following elements: >>> # [[nan, 0.3, 0.5, 0.9] >>> # [0.1, 0.2, -nan, 0.7]] >>> # Each example is followed by the corresponding output tensor. >>> x = paddle.to_tensor([[float('nan'), 0.3, 0.5, 0.9], ... [0.1, 0.2, float('-nan'), 0.7]],dtype="float32") >>> out1 = paddle.nansum(x) >>> out1 Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 2.69999981) >>> out2 = paddle.nansum(x, axis=0) >>> out2 Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [0.10000000, 0.50000000, 0.50000000, 1.59999990]) >>> out3 = paddle.nansum(x, axis=-1) >>> out3 Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True, [1.70000005, 1. ]) >>> out4 = paddle.nansum(x, axis=1, keepdim=True) >>> out4 Tensor(shape=[2, 1], dtype=float32, place=Place(cpu), stop_gradient=True, [[1.70000005], [1. ]]) >>> # y is a Tensor with shape [2, 2, 2] and elements as below: >>> # [[[1, nan], [3, 4]], >>> # [[5, 6], [-nan, 8]]] >>> # Each example is followed by the corresponding output tensor. >>> y = paddle.to_tensor([[[1, float('nan')], [3, 4]], ... [[5, 6], [float('-nan'), 8]]]) >>> out5 = paddle.nansum(y, axis=[1, 2]) >>> out5 Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True, [8. , 19.]) >>> out6 = paddle.nansum(y, axis=[0, 1]) >>> out6 Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True, [9. , 18.])
-
narrow
(
dim: int,
start: int | Tensor,
length: int
)
Tensor
narrow¶
-
Returns a narrowed slice of input along a single axis.
This operator selects the index range [start, start + length) on dimension dim and keeps all the dimensions unchanged.
- Parameters
-
input (Tensor) – Input tensor.
dim (int) – Dimension to narrow. Supports negative indexing.
start (int|Tensor) – Start index on
dim. Can be a Python int or a 0-D int Tensor (int32 or int64). Negative values are supported.length (int) – Number of elements to select from
start. Must be non-negative.
- Returns
-
A tensor that is a narrowed view of
input. - Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.to_tensor([[1, 2, 3, 4], ... [5, 6, 7, 8]], dtype='int64') >>> y1 = paddle.narrow(x, dim=1, start=1, length=2) >>> print(y1) Tensor(shape=[2, 2], dtype=int64, place=Place(cpu), stop_gradient=True, [[2, 3], [6, 7]]) >>> y2 = paddle.narrow(x, dim=-1, start=-3, length=3) >>> print(y2) Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[2, 3, 4], [6, 7, 8]]) >>> s = paddle.to_tensor(0, dtype='int64') >>> y3 = paddle.narrow(x, dim=1, start=s, length=2) >>> print(y3) Tensor(shape=[2, 2], dtype=int64, place=Place(cpu), stop_gradient=True, [[1, 2], [5, 6]])
- property ndim
-
Returns the dimension of current Variable
- Returns
-
the dimension
Examples
>>> import paddle >>> paddle.enable_static() >>> # create a static Variable >>> x = paddle.static.data(name='x', shape=[3, 2, 1]) >>> # print the dimension of the Variable >>> print(x.ndim) 3
-
ndimension
(
)
ndimension¶
-
Returns the dimension of current Variable
- Returns
-
the dimension
Examples
>>> import paddle >>> paddle.enable_static() >>> # create a static Variable >>> x = paddle.static.data(name='x', shape=[3, 2, 1]) >>> # print the dimension of the Variable >>> print(x.ndimension()) 3
-
neg
(
name: str | None = None
)
Tensor
neg¶
-
This function computes the negative of the Tensor elementwisely.
- Parameters
-
x (Tensor) – Input of neg operator, an N-D Tensor, with data type bfloat16, float16, float32, float64, int8, int16, int32, int64, uint8, complex64, complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
The negative of input Tensor. The shape and data type are the same with input Tensor.
- Return type
-
out (Tensor)
Examples
>>> import paddle >>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3]) >>> out = paddle.neg(x) >>> out Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [ 0.40000001, 0.20000000, -0.10000000, -0.30000001])
-
neg_
(
name: str | None = None
)
Tensor
neg_¶
-
Inplace version of
negAPI, the output Tensor will be inplaced with inputx. Please refer to neg.
-
negative
(
name: str | None = None
)
Tensor
negative¶
-
Returns the negated version of the input Tensor. This is used in Tensor.__neg__, applying the unary - operator to the tensor.
\[Out = -X\]- Parameters
-
x (Tensor) – The input tensor. The tensor cannot be of type bool.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
- A tensor with the same shape and data type as the input tensor. The returned tensor
-
is the negative.
- Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.to_tensor([-1, 0, 1]) >>> out = paddle.negative(x) >>> print(out) Tensor(shape=[3], dtype=int64, place=Place(cpu), stop_gradient=True, [1, 0, -1])
-
nextafter
(
y: Tensor,
name: str | None = None
)
Tensor
nextafter¶
-
Return the next floating-point value after input towards other, elementwise. The shapes of input and other must be broadcastable.
- Parameters
-
x (Tensor) – An N-D Tensor, the data type is float32, float64.
y (Tensor) – An N-D Tensor, the data type is float32, float64.
name (str, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
An N-D Tensor, the shape and data type is the same with input.
- Return type
-
out (Tensor)
Examples
>>> import paddle >>> out = paddle.nextafter(paddle.to_tensor([1.0,2.0]),paddle.to_tensor([2.0,1.0])) >>> out Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True, [1.00000012, 1.99999988])
-
nonzero
(
as_tuple=False,
*,
out: Tensor | None = None
)
nonzero¶
-
Return a tensor containing the indices of all non-zero elements of the input tensor. If as_tuple is True, return a tuple of 1-D tensors, one for each dimension in input, each containing the indices (in that dimension) of all non-zero elements of input. Given a n-Dimensional input tensor with shape [x_1, x_2, …, x_n], If as_tuple is False, we can get a output tensor with shape [z, n], where z is the number of all non-zero elements in the input tensor. If as_tuple is True, we can get a 1-D tensor tuple of length n, and the shape of each 1-D tensor is [z, 1].
Note
Alias Support: The parameter name
inputcan be used as an alias forx. For example,nonzero(input=tensor_x)is equivalent tononzero(x=tensor_x).- Parameters
-
x (Tensor) – The input tensor variable. alias:
input.as_tuple (bool, optional) – Return type, Tensor or tuple of Tensor.
out (Tensor|None, optional) – The output tensor. Default: None.
- Returns
-
Tensor or tuple of Tensor, The data type is int64.
Examples
>>> import paddle >>> x1 = paddle.to_tensor([[1.0, 0.0, 0.0], ... [0.0, 2.0, 0.0], ... [0.0, 0.0, 3.0]]) >>> x2 = paddle.to_tensor([0.0, 1.0, 0.0, 3.0]) >>> out_z1 = paddle.nonzero(x1) >>> print(out_z1) Tensor(shape=[3, 2], dtype=int64, place=Place(cpu), stop_gradient=True, [[0, 0], [1, 1], [2, 2]]) >>> out_z1_tuple = paddle.nonzero(x1, as_tuple=True) >>> for out in out_z1_tuple: ... print(out) Tensor(shape=[3], dtype=int64, place=Place(cpu), stop_gradient=True, [0, 1, 2]) Tensor(shape=[3], dtype=int64, place=Place(cpu), stop_gradient=True, [0, 1, 2]) >>> out_z2 = paddle.nonzero(x2) >>> print(out_z2) Tensor(shape=[2, 1], dtype=int64, place=Place(cpu), stop_gradient=True, [[1], [3]]) >>> out_z2_tuple = paddle.nonzero(x2, as_tuple=True) >>> for out in out_z2_tuple: ... print(out) Tensor(shape=[2], dtype=int64, place=Place(cpu), stop_gradient=True, [1, 3])
-
norm
(
p: float | _POrder | None = None,
axis: int | list[int] | tuple[int, int] | None = None,
keepdim: bool = False,
out: paddle.Tensor | None = None,
dtype: paddle._typing.DTypeLike | None = None,
name: str | None = None
)
Tensor
norm¶
-
Returns the matrix norm (the Frobenius norm, the nuclear norm and p-norm) or vector norm (the 1-norm, the Euclidean or 2-norm, and in general the p-norm) of a given tensor.
Whether the function calculates the vector norm or the matrix norm is determined as follows:
If axis is of type int, calculate the vector norm.
If axis is a two-dimensional array, calculate the matrix norm.
If axis is None, x is compressed into a one-dimensional vector and the vector norm is calculated.
Paddle supports the following norms:
porder
norm for matrices
norm for vectors
None(default)
frobenius norm
2_norm
fro
frobenius norm
not support
nuc
nuclear norm
not support
inf
max(sum(abs(x), dim=1))
max(abs(x))
-inf
min(sum(abs(x), dim=1))
min(abs(x))
0
not support
sum(x != 0)
1
max(sum(abs(x), dim=0))
as below
-1
min(sum(abs(x), dim=0))
as below
2
The maximum singular value of a matrix consisting of axis.
as below
-2
The minimum singular value of a matrix consisting of axis.
as below
- other int
-
or float
not support
sum(abs(x)^{porder})^ {(1 / porder)}
Note
Alias Support: The parameter name
inputcan be used as an alias forx, anddimcan be used as an alias foraxis. For example,norm(input=tensor_x, dim=1, ...)is equivalent tonorm(x=tensor_x, axis=1, ...).- Parameters
-
x (Tensor) – The input tensor could be N-D tensor, and the input data type could be float32 or float64. alias:
input.p (int|float|string|None, optional) – Order of the norm. Supported values are fro, nuc, 0, ±1, ±2, ±inf and any real number yielding the corresponding p-norm. Default value is None.
axis (int|list|tuple, optional) – The axis on which to apply norm operation. If axis is int or list(int)/tuple(int) with only one element, the vector norm is computed over the axis. If axis < 0, the dimension to norm operation is rank(input) + axis. If axis is a list(int)/tuple(int) with two elements, the matrix norm is computed over the axis. Default value is None. alias:
dim.keepdim (bool, optional) – Whether to reserve the reduced dimension in the output Tensor. The result tensor will have fewer dimension than the
inputunlesskeepdimis true, default value is False.out (Tensor, optional) – The output tensor. Ignored out = None.
dtype (DTypeLike | None, optional) – The data type of the output tensor. If specified, the input tensor is casted to dtype while performing the operation. Default value is None.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
- Returns
-
results of norm operation on the specified axis of input tensor, it’s data type is the same as input’s Tensor.
- Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.arange(24, dtype="float32").reshape([2, 3, 4]) - 12 >>> print(x) Tensor(shape=[2, 3, 4], dtype=float32, place=Place(cpu), stop_gradient=True, [[[-12., -11., -10., -9. ], [-8. , -7. , -6. , -5. ], [-4. , -3. , -2. , -1. ]], [[ 0. , 1. , 2. , 3. ], [ 4. , 5. , 6. , 7. ], [ 8. , 9. , 10., 11.]]]) >>> # compute frobenius norm along last two dimensions. >>> out_fro = paddle.linalg.norm(x, p='fro', axis=[0,1]) >>> print(out_fro) Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [17.43559647, 16.91153526, 16.73320007, 16.91153526]) >>> # compute 2-order vector norm along last dimension. >>> out_pnorm = paddle.linalg.norm(x, p=2, axis=-1) >>> print(out_pnorm) Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True, [[21.11871147, 13.19090557, 5.47722578 ], [3.74165750 , 11.22497177, 19.13112640]]) >>> # compute 2-order norm along [0,1] dimension. >>> out_pnorm = paddle.linalg.norm(x, p=2, axis=[0,1]) >>> print(out_pnorm) Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [15.75857544, 14.97978878, 14.69693947, 14.97978973]) >>> # compute inf-order norm >>> out_pnorm = paddle.linalg.norm(x, p=float("inf")) >>> print(out_pnorm) Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 12.) >>> out_pnorm = paddle.linalg.norm(x, p=float("inf"), axis=0) >>> print(out_pnorm) Tensor(shape=[3, 4], dtype=float32, place=Place(cpu), stop_gradient=True, [[12., 11., 10., 9. ], [8. , 7. , 6. , 7. ], [8. , 9. , 10., 11.]]) >>> # compute -inf-order norm >>> out_pnorm = paddle.linalg.norm(x, p=-float("inf")) >>> print(out_pnorm) Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 0.) >>> out_pnorm = paddle.linalg.norm(x, p=-float("inf"), axis=0) >>> print(out_pnorm) Tensor(shape=[3, 4], dtype=float32, place=Place(cpu), stop_gradient=True, [[0., 1., 2., 3.], [4., 5., 6., 5.], [4., 3., 2., 1.]])
-
normal_
(
mean: complex = 0.0,
std: float = 1.0,
name: str | None = None
)
Tensor
normal_¶
-
This is the inplace version of api
normal, which returns a Tensor filled with random values sampled from a normal distribution. The output Tensor will be inplaced with inputx. Please refer to normal.- Parameters
-
x (Tensor) – The input tensor to be filled with random values.
mean (float|int|complex, optional) – Mean of the output tensor, default is 0.0.
std (float|int, optional) – Standard deviation of the output tensor, default is 1.0.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
- Returns
-
Tensor, A Tensor filled with random values sampled from a normal distribution with
meanandstd.
Examples
>>> import paddle >>> x = paddle.randn([3, 4]) >>> x.normal_() >>> >>> print(x) Tensor(shape=[3, 4], dtype=float32, place=Place(cpu), stop_gradient=True, [[ 0.06132207, 1.11349595, 0.41906244, -0.24858207], [-1.85169315, -1.50370061, 1.73954511, 0.13331604], [ 1.66359663, -0.55764782, -0.59911072, -0.57773495]])
-
not_equal
(
y: Tensor,
name: str | None = None
)
Tensor
not_equal¶
-
Returns the truth value of \(x != y\) elementwise, which is equivalent function to the overloaded operator !=.
Note
The output has no gradient.
- Parameters
-
x (Tensor) – First input to compare which is N-D tensor. The input data type should be bool, bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64, complex64, complex128.
y (Tensor) – Second input to compare which is N-D tensor. The input data type should be bool, bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64, complex64, complex128.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
- Returns
-
The output shape is same as input
x. The output data type is bool. - Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.to_tensor([1, 2, 3]) >>> y = paddle.to_tensor([1, 3, 2]) >>> result1 = paddle.not_equal(x, y) >>> print(result1) Tensor(shape=[3], dtype=bool, place=Place(cpu), stop_gradient=True, [False, True , True ])
-
not_equal_
(
y: Tensor,
name: str | None = None
)
Tensor
not_equal_¶
-
Inplace version of
not_equalAPI, the output Tensor will be inplaced with inputx. Please refer to not_equal.
-
numel
(
name: str | None = None
)
Tensor
numel¶
-
Returns the number of elements for a tensor, which is a 0-D int64 Tensor with shape [].
- Parameters
-
x (Tensor) – The input Tensor, it’s data type can be bool, float16, float32, float64, uint8, int8, int32, int64, complex64, complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
The number of elements for the input Tensor, whose shape is [].
- Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.full(shape=[4, 5, 7], fill_value=0, dtype='int32') >>> numel = paddle.numel(x) >>> print(numel.numpy()) 140
-
ormqr
(
tau: Tensor,
y: Tensor,
left: bool = True,
transpose: bool = False,
name: str | None = None
)
Tensor
ormqr¶
-
Calculate the product of a normal matrix and a householder matrix. Compute the product of the matrix C (given by y) with dimensions (m, n) and a matrix Q, where Q is generated by the Householder reflection coefficient (x, tau). Returns a Tensor.
- Parameters
-
x (Tensor) – Shape(*,mn, k), when left is True, the value of mn is equal to m, otherwise the value of mn is equal to n. * indicates that the length of the tensor on axis 0 is 0 or greater.
tau (Tensor) – Shape (*, min(mn, k)), where * indicates that the length of the Tensor on axis 0 is 0 or greater, and its type is the same as input.
y (Tensor) – Shape (*m,n), where * indicates that the length of the Tensor on axis 0 is 0 or greater, and its type is the same as input.
left (bool, optional) – Determines the order in which the matrix product operations are operated. If left is true, the order of evaluation is op(Q) * y, otherwise, the order of evaluation is y * op(Q). Default value: True.
transpose (bool, optional) – If true, the matrix Q is conjugated and transposed, otherwise, the conjugate transpose transformation is not performed. Default value: False.
name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Returns
-
Tensor. Data type and dimension are equals with
y.
Examples
>>> import paddle >>> import numpy as np >>> from paddle import linalg >>> input = paddle.to_tensor([[-114.6, 10.9, 1.1], [-0.304, 38.07, 69.38], [-0.45, -0.17, 62]]) >>> tau = paddle.to_tensor([1.55, 1.94, 3.0]) >>> y = paddle.to_tensor([[-114.6, 10.9, 1.1], [-0.304, 38.07, 69.38], [-0.45, -0.17, 62]]) >>> output = linalg.ormqr(input, tau, y) >>> print(output) Tensor(shape=[3, 3], dtype=float32, place=Place(cpu), stop_gradient=True, [[ 63.82712936 , -13.82312393 , -116.28614044], [-53.65926361 , -28.15783691 , -70.42700958 ], [-79.54292297 , 24.00182915 , -41.34253311 ]])
-
outer
(
y: Tensor,
name: str | None = None,
*,
out: Tensor | None = None
)
Tensor
outer¶
-
Outer product of two Tensors.
Input is flattened if not already 1-dimensional.
Note
Alias Support: The parameter name
inputcan be used as an alias forx, andvec2can be used as an alias fory. For example,outer(input=tensor_x, vec2=tensor_y, ...)is equivalent toouter(x=tensor_x, y=tensor_y, ...).- Parameters
-
x (Tensor) – An N-D Tensor or a Scalar Tensor. alias:
input.y (Tensor) – An N-D Tensor or a Scalar Tensor. alias:
vec2.name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
out (Tensor|None, optional) – The output Tensor. If set, the result will be stored in this Tensor.
- Returns
-
The outer-product Tensor.
- Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.arange(1, 4).astype('float32') >>> y = paddle.arange(1, 6).astype('float32') >>> out = paddle.outer(x, y) >>> print(out) Tensor(shape=[3, 5], dtype=float32, place=Place(cpu), stop_gradient=True, [[1. , 2. , 3. , 4. , 5. ], [2. , 4. , 6. , 8. , 10.], [3. , 6. , 9. , 12., 15.]])
-
pca_lowrank
(
q: int | None = None,
center: bool = True,
niter: int = 2,
name: str | None = None
)
tuple[Tensor, Tensor, Tensor]
pca_lowrank¶
-
Performs linear Principal Component Analysis (PCA) on a low-rank matrix or batches of such matrices.
Let \(X\) be the input matrix or a batch of input matrices, the output should satisfies:
\[X = U * diag(S) * V^{T}\]- Parameters
-
x (Tensor) – The input tensor. Its shape should be […, N, M], where … is zero or more batch dimensions. N and M can be arbitrary positive number. The data type of x should be float32 or float64.
q (int, optional) – a slightly overestimated rank of \(X\). Default value is \(q=min(6,N,M)\).
center (bool, optional) – if True, center the input tensor. Default value is True.
niter (int, optional) – number of iterations to perform. Default: 2.
name (str|None, optional) – Name for the operation. For more information, please refer to api_guide_Name. Default: None.
- Returns
-
Tensor U, is N x q matrix.
Tensor S, is a vector with length q.
Tensor V, is M x q matrix.
tuple (U, S, V): which is the nearly optimal approximation of a singular value decomposition of a centered matrix \(X\).
Examples
>>> import paddle >>> paddle.seed(2023) >>> x = paddle.randn((5, 5), dtype='float64') >>> U, S, V = paddle.linalg.pca_lowrank(x) >>> print(U) Tensor(shape=[5, 5], dtype=float64, place=Place(cpu), stop_gradient=True, [[ 0.80131563, 0.11962647, 0.27667179, -0.25891214, 0.44721360], [-0.12642301, 0.69917551, -0.17899393, 0.51296394, 0.44721360], [ 0.08997135, -0.69821706, -0.20059228, 0.51396579, 0.44721360], [-0.23871837, -0.02815453, -0.59888153, -0.61932365, 0.44721360], [-0.52614559, -0.09243040, 0.70179595, -0.14869394, 0.44721360]]) >>> print(S) Tensor(shape=[5], dtype=float64, place=Place(cpu), stop_gradient=True, [2.60101614, 2.40554940, 1.49768346, 0.19064830, 0.00000000]) >>> print(V) Tensor(shape=[5, 5], dtype=float64, place=Place(cpu), stop_gradient=True, [[ 0.58339481, -0.17143771, 0.00522143, 0.57976310, 0.54231640], [ 0.22334335, 0.72963474, -0.30148399, -0.39388750, 0.41438019], [ 0.05416913, 0.34666487, 0.93549758, 0.00063507, 0.04162998], [-0.39519094, 0.53074980, -0.16687419, 0.71175586, -0.16638919], [-0.67131070, -0.19071018, 0.07795789, -0.04615811, 0.71046714]])
-
permute
(
dims: Sequence[int]
)
Tensor
permute¶
-
Permute the dimensions of a tensor.
- Parameters
-
input (Tensor) – the input tensor.
*dims (tuple|list|int) – The desired ordering of dimensions. Supports passing as variable-length arguments (e.g., permute(x, 1, 0, 2)) or as a single list/tuple (e.g., permute(x, [1, 0, 2])).
- Returns
-
A tensor with permuted dimensions.
- Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.randn([2, 3, 4]) >>> y = paddle.permute(x, (1, 0, 2)) >>> print(y.shape) [3, 2, 4] >>> y = x.permute([1, 0, 2]) >>> print(y.shape) [3, 2, 4]
-
pinv
(
rcond: float | Tensor = 1e-15,
hermitian: bool = False,
name: str | None = None
)
Tensor
pinv¶
-
Calculate pseudo inverse via SVD(singular value decomposition) of one matrix or batches of regular matrix.
\[if hermitian == False: x = u * s * vt (SVD) out = v * 1/s * ut else: x = u * s * ut (eigh) out = u * 1/s * u.conj().transpose(-2,-1)\]If x is hermitian or symmetric matrix, svd will be replaced with eigh.
- Parameters
-
x (Tensor) – The input tensor. Its shape should be (*, m, n) where * is zero or more batch dimensions. m and n can be arbitrary positive number. The data type of x should be float32 or float64 or complex64 or complex128. When data type is complex64 or complex128, hermitian should be set True.
rcond (Tensor|float, optional) – the tolerance value to determine when is a singular value zero. Default:1e-15.
hermitian (bool, optional) – indicates whether x is Hermitian if complex or symmetric if real. Default: False.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
- Returns
-
The tensor with same data type with x. it represents pseudo inverse of x. Its shape should be (*, n, m).
- Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.arange(15).reshape((3, 5)).astype('float64') >>> input = paddle.to_tensor(x) >>> out = paddle.linalg.pinv(input) >>> print(input) Tensor(shape=[3, 5], dtype=float64, place=Place(cpu), stop_gradient=True, [[0. , 1. , 2. , 3. , 4. ], [5. , 6. , 7. , 8. , 9. ], [10., 11., 12., 13., 14.]]) >>> print(out) Tensor(shape=[5, 3], dtype=float64, place=Place(cpu), stop_gradient=True, [[-0.22666667, -0.06666667, 0.09333333], [-0.12333333, -0.03333333, 0.05666667], [-0.02000000, -0.00000000, 0.02000000], [ 0.08333333, 0.03333333, -0.01666667], [ 0.18666667, 0.06666667, -0.05333333]]) # one can verify : x * out * x = x ; # or out * x * out = x ;
-
place
(
)
place¶
-
Variable don’t have ‘place’ interface in static graph mode But this interface can greatly facilitate dy2static. So we give a warning here and return None.
-
polar
(
angle: Tensor,
name: Optional[str] = None,
*,
out: Optional[Tensor] = None
)
Tensor
polar¶
-
Return a Cartesian coordinates corresponding to the polar coordinates complex tensor given the
absandanglecomponent.- Parameters
-
abs (Tensor) – The abs component. The data type should be ‘float32’ or ‘float64’.
angle (Tensor) – The angle component. The data type should be the same as
abs.name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
out (Tensor, optional) – The output tensor. If set, the result will be stored in this tensor. Default is None.
- Returns
-
Tensor, The output tensor. The data type is ‘complex64’ or ‘complex128’, with the same precision as
absandangle.
Note
paddle.polarsupports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .Examples
>>> import paddle >>> import numpy as np >>> abs = paddle.to_tensor([1, 2], dtype=paddle.float64) >>> angle = paddle.to_tensor([np.pi / 2, 5 * np.pi / 4], dtype=paddle.float64) >>> out = paddle.polar(abs, angle) >>> print(out) Tensor(shape=[2], dtype=complex128, place=Place(cpu), stop_gradient=True, [ (6.123233995736766e-17+1j) , (-1.4142135623730954-1.414213562373095j)])
-
polygamma
(
n: int,
name: str | None = None
)
Tensor
polygamma¶
-
Calculates the polygamma of the given input tensor, element-wise.
The equation is:
\[\Phi^n(x) = \frac{d^n}{dx^n} [\ln(\Gamma(x))]\]- Parameters
-
x (Tensor) – Input Tensor. Must be one of the following types: float32, float64, uint8, int8, int16, int32, int64.
n (int) – Order of the derivative. Must be integral.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
-
- out (Tensor), A Tensor. the polygamma of the input Tensor, the shape and data type is the same with input
-
(integer types are autocasted into float32).
-
Examples
>>> import paddle >>> data = paddle.to_tensor([2, 3, 25.5], dtype='float32') >>> res = paddle.polygamma(data, 1) >>> print(res) Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True, [0.64493412, 0.39493406, 0.03999467])
-
polygamma_
(
n: int,
name: str | None = None
)
Tensor
polygamma_¶
-
Inplace version of
polygammaAPI, the output Tensor will be inplaced with inputx. Please refer to polygamma.
-
pop
(
*args
)
pop¶
-
The type variable must be LoD Tensor Array. When self is DenseTensorArray, calling pop is similar to Python’s pop on list. This interface is used to simplify dygraph to static graph operations.
- Parameters
-
self (Variable) – The source variable, which must be DENSE_TENSOR_ARRAY
*args – optional, a int means index.
- Returns
-
self[index]
- Return type
-
Variable
-
pow
(
y: float | Tensor,
name: str | None = None,
*,
out: Tensor | None = None
)
Tensor
pow¶
-
Compute the power of Tensor elements. The equation is:
\[out = x^{y}\]Note
paddle.powsupports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .Note
Alias Support: The parameter name
inputcan be used as an alias forx, The parameter nameexponentcan be used as an alias fory. For example,pow(input=2, exponent=1.1)is equivalent topow(x=2, y=1.1).- Parameters
-
x (Tensor) – An N-D Tensor, the data type is bfloat16, float16, float32, float64, int32, int64, complex64 or complex128.
input – An alias for
x, with identical behavior.y (float|int|Tensor) – If it is an N-D Tensor, its data type should be the same as x.
exponent – An alias for
y, with identical behavior.name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
out (Tensor, optional) – The output tensor. If set, the result will be stored in this tensor. Default is None.
- Returns
-
N-D Tensor. A location into which the result is stored. Its dimension and data type are the same as x.
Examples
>>> import paddle >>> x = paddle.to_tensor([1, 2, 3], dtype='float32') >>> # example 1: y is a float or int >>> res = paddle.pow(x, 2) >>> print(res) Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True, [1., 4., 9.]) >>> res = paddle.pow(x, 2.5) >>> print(res) Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True, [1. , 5.65685415 , 15.58845711]) >>> # example 2: y is a Tensor >>> y = paddle.to_tensor([2], dtype='float32') >>> res = paddle.pow(x, y) >>> print(res) Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True, [1., 4., 9.])
-
pow_
(
y: float | Tensor,
name: str | None = None
)
Tensor
pow_¶
-
Inplace version of
powAPI, the output Tensor will be inplaced with inputx. Please refer to pow.
-
prod
(
axis: int | Sequence[int] | None = None,
keepdim: bool = False,
dtype: DTypeLike | None = None,
name: str | None = None
)
Tensor
prod¶
-
Compute the product of tensor elements over the given axis.
Note
Alias Support: The parameter name
inputcan be used as an alias forx, anddimcan be used as an alias foraxis. For example,prod(input=tensor_x, dim=1, ...)is equivalent toprod(x=tensor_x, axis=1, ...).- Parameters
-
x (Tensor) – The input tensor, its data type should be bfloat16, float16, float32, float64, int32, int64, complex64, complex128. alias:
input.axis (int|list|tuple|None, optional) – The axis along which the product is computed. If
None, multiply all elements of x and return a Tensor with a single element, otherwise must be in the range \([-x.ndim, x.ndim)\). If \(axis[i]<0\), the axis to reduce is \(x.ndim + axis[i]\). Default is None. alias:dim.keepdim (bool, optional) – Whether to reserve the reduced dimension in the output Tensor. The result tensor will have one fewer dimension than the input unless keepdim is true. Default is False.
dtype (str|core.VarDesc.VarType|core.DataType|np.dtype, optional) – The desired date type of returned tensor, can be bfloat16, float16, float32, float64, int32, int64. If specified, the input tensor is casted to dtype before operator performed. This is very useful for avoiding data type overflows. The default value is None, the dtype of output is the same as input Tensor x.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, result of product on the specified dim of input tensor.
Examples
>>> import paddle >>> # the axis is a int element >>> x = paddle.to_tensor([[0.2, 0.3, 0.5, 0.9], ... [0.1, 0.2, 0.6, 0.7]]) >>> out1 = paddle.prod(x) >>> out1 Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 0.00022680) >>> out2 = paddle.prod(x, -1) >>> out2 Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True, [0.02700000, 0.00840000]) >>> out3 = paddle.prod(x, 0) >>> out3 Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [0.02000000, 0.06000000, 0.30000001, 0.63000000]) >>> out4 = paddle.prod(x, 0, keepdim=True) >>> out4 Tensor(shape=[1, 4], dtype=float32, place=Place(cpu), stop_gradient=True, [[0.02000000, 0.06000000, 0.30000001, 0.63000000]]) >>> out5 = paddle.prod(x, 0, dtype='int64') >>> out5 Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True, [0, 0, 0, 0]) >>> # the axis is list >>> y = paddle.to_tensor([[[1.0, 2.0], [3.0, 4.0]], ... [[5.0, 6.0], [7.0, 8.0]]]) >>> out6 = paddle.prod(y, [0, 1]) >>> out6 Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True, [105., 384.]) >>> out7 = paddle.prod(y, (1, 2)) >>> out7 Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True, [24. , 1680.])
-
put_along_axis
(
indices: Tensor,
values: float | Tensor,
axis: int,
reduce: Literal['assign', 'add', 'mul', 'multiply', 'mean', 'amin', 'amax'] = 'assign',
include_self: bool = True,
broadcast: bool = True
)
Tensor
put_along_axis¶
-
Put values into the destination array by given indices matrix along the designated axis.
- Parameters
-
arr (Tensor) – The Destination Tensor. Supported data types are bfloat16, float16, float32, float64, int32, int64, uint8.
indices (Tensor) – Indices to put along each 1d slice of arr. This must match the dimension of arr, and need to broadcast against arr if broadcast is ‘True’. Supported data type are int32 and int64.
values (scalar|Tensor) – The value element(s) to put. The data types should be same as arr.
axis (int) – The axis to put 1d slices along.
reduce (str, optional) – The reduce operation, default is ‘assign’, support ‘add’, ‘assign’, ‘mul’, ‘multiply’, ‘mean’, ‘amin’ and ‘amax’.
include_self (bool, optional) – whether to reduce with the elements of arr, default is ‘True’.
broadcast (bool, optional) – whether to broadcast indices, default is ‘True’.
- Returns
-
Tensor, The indexed element, same dtype with arr
Examples
>>> import paddle >>> x = paddle.to_tensor([[10, 30, 20], [60, 40, 50]]) >>> index = paddle.to_tensor([[0]]) >>> value = 99 >>> axis = 0 >>> result = paddle.put_along_axis(x, index, value, axis) >>> print(result) Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[99, 99, 99], [60, 40, 50]]) >>> index = paddle.zeros((2,2)).astype("int32") >>> value=paddle.to_tensor([[1,2],[3,4]]).astype(x.dtype) >>> result = paddle.put_along_axis(x, index, value, 0, "add", True, False) >>> print(result) Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[14, 36, 20], [60, 40, 50]]) >>> result = paddle.put_along_axis(x, index, value, 0, "mul", True, False) >>> print(result) Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[30 , 240, 20 ], [60 , 40 , 50 ]]) >>> result = paddle.put_along_axis(x, index, value, 0, "mean", True, False) >>> print(result) Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[4 , 12, 20], [60, 40, 50]]) >>> result = paddle.put_along_axis(x, index, value, 0, "amin", True, False) >>> print(result) Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[1 , 2 , 20], [60, 40, 50]]) >>> result = paddle.put_along_axis(x, index, value, 0, "amax", True, False) >>> print(result) Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[10, 30, 20], [60, 40, 50]]) >>> result = paddle.put_along_axis(x, index, value, 0, "add", False, False) >>> print(result) Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[4 , 6 , 20], [60, 40, 50]])
-
put_along_axis_
(
indices: Tensor,
values: float | Tensor,
axis: int,
reduce: Literal['assign', 'add', 'mul', 'multiply', 'mean', 'amin', 'amax'] = 'assign',
include_self: bool = True,
broadcast: bool = True
)
put_along_axis_¶
-
Inplace version of
put_along_axisAPI, the output Tensor will be inplaced with inputarr. Please refer to put_along_axis.
-
qr
(
mode='reduced',
name=None
)
Tensor | tuple[Tensor, Tensor]
qr¶
-
Computes the QR decomposition of one matrix or batches of matrices (backward is unsupported now).
- Parameters
-
x (Tensor) – The input tensor. Its shape should be […, M, N], where … is zero or more batch dimensions. M and N can be arbitrary positive number. The data type of x supports float, double, complex64, complex128.
mode (str, optional) – A flag to control the behavior of qr. Suppose x’s shape is […, M, N] and denoting K = min(M, N): If mode = “reduced”, qr op will return reduced Q and R matrices, which means Q’s shape is […, M, K] and R’s shape is […, K, N]. If mode = “complete”, qr op will return complete Q and R matrices, which means Q’s shape is […, M, M] and R’s shape is […, M, N]. If mode = “r”, qr op will only return reduced R matrix, which means R’s shape is […, K, N]. Default: “reduced”.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
If mode = “reduced” or mode = “complete”, qr will return a two tensor-tuple, which represents Q and R. If mode = “r”, qr will return a tensor which represents R.
Examples
>>> import paddle >>> x = paddle.to_tensor([[1.0, 2.0], [3.0, 4.0], [5.0, 6.0]]).astype('float64') >>> q, r = paddle.linalg.qr(x) >>> print(q) Tensor(shape=[3, 2], dtype=float64, place=Place(cpu), stop_gradient=True, [[-0.16903085, 0.89708523], [-0.50709255, 0.27602622], [-0.84515425, -0.34503278]]) >>> print(r) Tensor(shape=[2, 2], dtype=float64, place=Place(cpu), stop_gradient=True, [[-5.91607978, -7.43735744], [ 0. , 0.82807867]]) >>> # one can verify : X = Q * R ;
-
quantile
(
q: float | Sequence[float] | Tensor,
axis: int | list[int] | None = None,
keepdim: bool = False,
interpolation: _Interpolation = 'linear'
)
Tensor
quantile¶
-
Compute the quantile of the input along the specified axis. If any values in a reduced row are NaN, then the quantiles for that reduction will be NaN.
- Parameters
-
x (Tensor) – The input Tensor, it’s data type can be float32, float64, int32, int64.
q (int|float|list|Tensor) – The q for calculate quantile, which should be in range [0, 1]. If q is a list or a 1-D Tensor, each element of q will be calculated and the first dimension of output is same to the number of
q. If q is a 0-D Tensor, it will be treated as an integer or float.axis (int|list, optional) – The axis along which to calculate quantile.
axisshould be int or list of int.axisshould be in range [-D, D), where D is the dimensions ofx. Ifaxisis less than 0, it works the same way as \(axis + D\). Ifaxisis a list, quantile is calculated over all elements of given axes. Ifaxisis None, quantile is calculated over all elements ofx. Default is None.keepdim (bool, optional) – Whether to reserve the reduced dimension(s) in the output Tensor. If
keepdimis True, the dimensions of the output Tensor is the same asxexcept in the reduced dimensions(it is of size 1 in this case). Otherwise, the shape of the output Tensor is squeezed inaxis. Default is False.interpolation (str, optional) – The interpolation method to use when the desired quantile falls between two data points. Must be one of linear, higher, lower, midpoint and nearest. Default is linear.
name (str, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, results of quantile along
axisofx.
Examples
>>> import paddle >>> y = paddle.arange(0, 8 ,dtype="float32").reshape([4, 2]) >>> print(y) Tensor(shape=[4, 2], dtype=float32, place=Place(cpu), stop_gradient=True, [[0., 1.], [2., 3.], [4., 5.], [6., 7.]]) >>> y1 = paddle.quantile(y, q=0.5, axis=[0, 1]) >>> print(y1) Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 3.50000000) >>> y2 = paddle.quantile(y, q=0.5, axis=1) >>> print(y2) Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [0.50000000, 2.50000000, 4.50000000, 6.50000000]) >>> y3 = paddle.quantile(y, q=[0.3, 0.5], axis=0) >>> print(y3) Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True, [[1.80000000, 2.80000000], [3. , 4. ]]) >>> y[0,0] = float("nan") >>> y4 = paddle.quantile(y, q=0.8, axis=1, keepdim=True) >>> print(y4) Tensor(shape=[4, 1], dtype=float32, place=Place(cpu), stop_gradient=True, [[nan ], [2.80000000], [4.80000000], [6.80000000]])
-
rad2deg
(
name: str | None = None
)
Tensor
rad2deg¶
-
Convert each of the elements of input x from angles in radians to degrees.
- Equation:
-
\[rad2deg(x)=180/ \pi * x\]
- Parameters
-
x (Tensor) – An N-D Tensor, the data type is float32, float64, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
An N-D Tensor, the shape and data type is the same with input (The output data type is float32 when the input data type is int).
- Return type
-
out (Tensor)
Examples
>>> import paddle >>> import math >>> x1 = paddle.to_tensor([3.142, -3.142, 6.283, -6.283, 1.570, -1.570]) >>> result1 = paddle.rad2deg(x1) >>> result1 Tensor(shape=[6], dtype=float32, place=Place(cpu), stop_gradient=True, [ 180.02334595, -180.02334595, 359.98937988, -359.98937988, 89.95437622 , -89.95437622 ]) >>> x2 = paddle.to_tensor(math.pi/2) >>> result2 = paddle.rad2deg(x2) >>> result2 Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 90.) >>> x3 = paddle.to_tensor(1) >>> result3 = paddle.rad2deg(x3) >>> result3 Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 57.29578018)
-
rank
(
)
Tensor
rank¶
-
Returns the number of dimensions for a tensor, which is a 0-D int32 Tensor.
- Parameters
-
input (Tensor) – The input Tensor with shape of \([N_1, N_2, ..., N_k]\), the data type is arbitrary.
- Returns
-
The 0-D tensor with the dimensions of the input Tensor.
- Return type
-
Tensor, the output data type is int32.
Examples
>>> import paddle >>> input = paddle.rand((3, 100, 100)) >>> rank = paddle.rank(input) >>> print(rank.numpy()) 3
-
ravel
(
)
Tensor
ravel¶
-
Return a contiguous flattened tensor. A copy is made only if needed. .. note:
The output Tensor will share data with origin Tensor and doesn't have a Tensor copy in ``dygraph`` mode. If you want to use the Tensor copy version, please use `Tensor.clone` like ``ravel_clone_x = x.ravel().clone()``. For example: .. code-block:: text Case 1: Given X.shape = (3, 100, 100, 4) We get: Out.shape = (3 * 100 * 100 * 4)- Parameters
-
x (Tensor) – A tensor of number of dimensions >= axis. A tensor with data type float16, float32, float64, int8, int32, int64, uint8.
- Returns
-
A tensor with the contents of the input tensor, whose input axes are flattened by indicated
start_axisandstop_axis, and data type is the same as inputx. - Return type
-
Tensor
Examples
>>> import paddle >>> image_shape=(2, 3, 4, 4) >>> x = paddle.arange(end=image_shape[0] * image_shape[1] * image_shape[2] * image_shape[3]) >>> img = paddle.reshape(x, image_shape) >>> out = paddle.ravel(img) >>> print(out.shape) [96]
-
real
(
name: str | None = None
)
Tensor
real¶
-
Returns a new Tensor containing real values of the input Tensor.
- Parameters
-
x (Tensor) – the input Tensor, its data type could be complex64 or complex128.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name .
- Returns
-
a Tensor containing real values of the input Tensor.
- Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.to_tensor( ... [[1 + 6j, 2 + 5j, 3 + 4j], [4 + 3j, 5 + 2j, 6 + 1j]]) >>> print(x) Tensor(shape=[2, 3], dtype=complex64, place=Place(cpu), stop_gradient=True, [[(1+6j), (2+5j), (3+4j)], [(4+3j), (5+2j), (6+1j)]]) >>> real_res = paddle.real(x) >>> print(real_res) Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True, [[1., 2., 3.], [4., 5., 6.]]) >>> real_t = x.real() >>> print(real_t) Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True, [[1., 2., 3.], [4., 5., 6.]])
-
reciprocal
(
name: str | None = None
)
Tensor
reciprocal¶
-
Reciprocal Activation Operator.
\[out = \frac{1}{x}\]- Parameters
-
x (Tensor) – Input of Reciprocal operator, an N-D Tensor, with data type float32, float64, float16, bfloat16, uint8, int8, int16, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
- Tensor. Output of Reciprocal operator, a Tensor with shape same as input
-
(integer types are autocasted into float32).
Examples
>>> import paddle >>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3]) >>> out = paddle.reciprocal(x) >>> print(out) Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [-2.50000000, -5. , 10. , 3.33333325])
-
reciprocal_
(
name=None
)
reciprocal_¶
-
Inplace version of
reciprocalAPI, the output Tensor will be inplaced with inputx. Please refer to reciprocal.
-
reduce_as
(
target: Tensor,
name: str | None = None
)
Tensor
reduce_as¶
-
Computes the sum of tensor elements make the shape of its result equal to the shape of target.
- Parameters
-
x (Tensor) – An N-D Tensor, the data type is bool, float16, float32, float64, int8, uint8, int16, uint16, int32, int64, complex64 or complex128.
target (Tensor) – An N-D Tensor, the length of x shape must greater than or equal to the length of target shape. The data type is bool, float16, float32, float64, int8, uint8, int16, uint16, int32, int64, complex64 or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
The sum of the input tensor x along some axis has the same shape as the shape of the input tensor target, if x.dtype=’bool’, x.dtype=’int32’, it’s data type is ‘int64’, otherwise it’s data type is the same as x.
- Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.to_tensor([[1, 2, 3, 4], [5, 6, 7, 8]]) >>> x Tensor(shape=[2, 4], dtype=int64, place=Place(gpu:0), stop_gradient=True, [[1, 2, 3, 4], [5, 6, 7, 8]]) >>> target = paddle.to_tensor([1, 2, 3, 4]) >>> target Tensor(shape=[4], dtype=int64, place=Place(gpu:0), stop_gradient=True, [1, 2, 3, 4]) >>> res = paddle.reduce_as(x, target) >>> res Tensor(shape=[4], dtype=int64, place=Place(gpu:0), stop_gradient=True, [6 , 8 , 10, 12])
-
remainder
(
y: Tensor,
name: str | None = None
)
Tensor
remainder¶
-
Mod two tensors element-wise. The equation is:
\[out = x \% y\]Note
paddle.remaindersupports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .And mod, floor_mod are all functions with the same name
- Parameters
-
x (Tensor) – the input tensor, it’s data type should be bfloat16, float16, float32, float64, int32, int64.
y (Tensor) – the input tensor, it’s data type should be bfloat16, float16, float32, float64, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
N-D Tensor. A location into which the result is stored. If x, y have different shapes and are “broadcastable”, the resulting tensor shape is the shape of x and y after broadcasting. If x, y have the same shape, its shape is the same as x and y.
Examples
>>> import paddle >>> x = paddle.to_tensor([2, 3, 8, 7]) >>> y = paddle.to_tensor([1, 5, 3, 3]) >>> z = paddle.remainder(x, y) >>> print(z) Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True, [0, 3, 2, 1]) >>> z = paddle.floor_mod(x, y) >>> print(z) Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True, [0, 3, 2, 1]) >>> z = paddle.mod(x, y) >>> print(z) Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True, [0, 3, 2, 1])
-
remainder_
(
y: Tensor,
name: str | None = None
)
Tensor
remainder_¶
-
Inplace version of
floor_mod_API, the output Tensor will be inplaced with inputx. Please refer to floor_mod_.
-
renorm
(
p: float,
axis: int,
max_norm: float
)
Tensor
renorm¶
-
renorm
This operator is used to calculate the p-norm along the axis, suppose the input-shape on axis dimension has the value of T, then the tensor is split into T parts, the p-norm should be calculated for each part, if the p-norm for part i is larger than max-norm, then each element in part i should be re-normalized at the same scale so that part-i’ p-norm equals max-norm exactly, otherwise part-i stays unchanged.
- Parameters
-
x (Tensor) – The input Tensor
p (float) – The power of the norm operation.
axis (int) – the dimension to slice the tensor.
max-norm (float) – the maximal norm limit.
- Returns
-
the renorm Tensor.
- Return type
-
Tensor
Examples
>>> import paddle >>> input = [[[2.0, 2.0, -2.0], [3.0, 0.3, 3.0]], ... [[2.0, -8.0, 2.0], [3.1, 3.7, 3.0]]] >>> x = paddle.to_tensor(input,dtype='float32') >>> y = paddle.renorm(x, 1.0, 2, 2.05) >>> print(y) Tensor(shape=[2, 2, 3], dtype=float32, place=Place(cpu), stop_gradient=True, [[[ 0.40594056, 0.29285714, -0.41000000], [ 0.60891086, 0.04392857, 0.61500001]], [[ 0.40594056, -1.17142856, 0.41000000], [ 0.62920785, 0.54178572, 0.61500001]]])
-
renorm_
(
p: float,
axis: int,
max_norm: float
)
Tensor
renorm_¶
-
Inplace version of
renormAPI, the output Tensor will be inplaced with inputx. Please refer to renorm.
-
repeat
(
repeats: int | Sequence[int] | Tensor
)
Tensor
repeat¶
-
Repeat elements of a tensor along specified dimensions.
- Parameters
-
input (Tensor) – The input tensor to be repeated.
*repeats (int|list|tuple|Tensor) – The number of times to repeat along each dimension. Can be a single integer (applies to the first dimension only), or multiple integers (one per dimension).
- Returns
-
The repeated tensor with expanded dimensions.
- Return type
-
Tensor
Note
When using a single integer, it only repeats along the first dimension. The total number of repeat values must match the number of dimensions in the tensor when using multiple values.
Examples
>>> import paddle >>> # Example 1: 1D tensor - single repeat >>> x = paddle.to_tensor([1, 2, 3]) >>> out = x.repeat(2) >>> print(out) Tensor(shape=[6], dtype=int64, place=Place(cpu), stop_gradient=True, [1, 2, 3, 1, 2, 3]) >>> # Example 2: 2D tensor - single repeat value >>> x = paddle.to_tensor([[1, 2], [3, 4]]) >>> out = x.repeat(2) >>> print(out) Tensor(shape=[2, 4], dtype=int64, place=Place(gpu:0), stop_gradient=True, [[1, 2, 1, 2], [3, 4, 3, 4]]) >>> # Example 3: 2D tensor - multiple repeats >>> x = paddle.to_tensor([[1, 2], [3, 4]]) >>> out = x.repeat([2, 3]) >>> print(out) Tensor(shape=[4, 6], dtype=int64, place=Place(gpu:0), stop_gradient=True, [[1, 2, 1, 2, 1, 2], [3, 4, 3, 4, 3, 4], [1, 2, 1, 2, 1, 2], [3, 4, 3, 4, 3, 4]]) >>> # Example 4: 3D tensor - mixed repeats >>> x = paddle.to_tensor([[[1, 2], [3, 4]]]) >>> out = x.repeat([2, 1, 3]) >>> print(out) Tensor(shape=[2, 2, 6], dtype=int64, place=Place(gpu:0), stop_gradient=True, [[[1, 2, 1, 2, 1, 2], [3, 4, 3, 4, 3, 4]], [[1, 2, 1, 2, 1, 2], [3, 4, 3, 4, 3, 4]]])
-
repeat_interleave
(
repeats: int | Tensor,
axis: int | None = None,
name: str | None = None,
*,
output_size: int | None = None
)
Tensor
repeat_interleave¶
-
Returns a new tensor which repeats the
xtensor along dimensionaxisusing the entries inrepeatswhich is a int or a Tensor.The image illustrates a typical case of the repeat_interleave operation. Given a tensor
[[1, 2, 3], [4, 5, 6]], with the repeat countsrepeats = [3, 2, 1]and parameteraxis = 1, it means that the elements in the 1st column are repeated 3 times, the 2nd column is repeated 2 times, and the 3rd column is repeated 1 time.The final output is a 2D tensor:
[[1, 1, 1, 2, 2, 3], [4, 4, 4, 5, 5, 6]].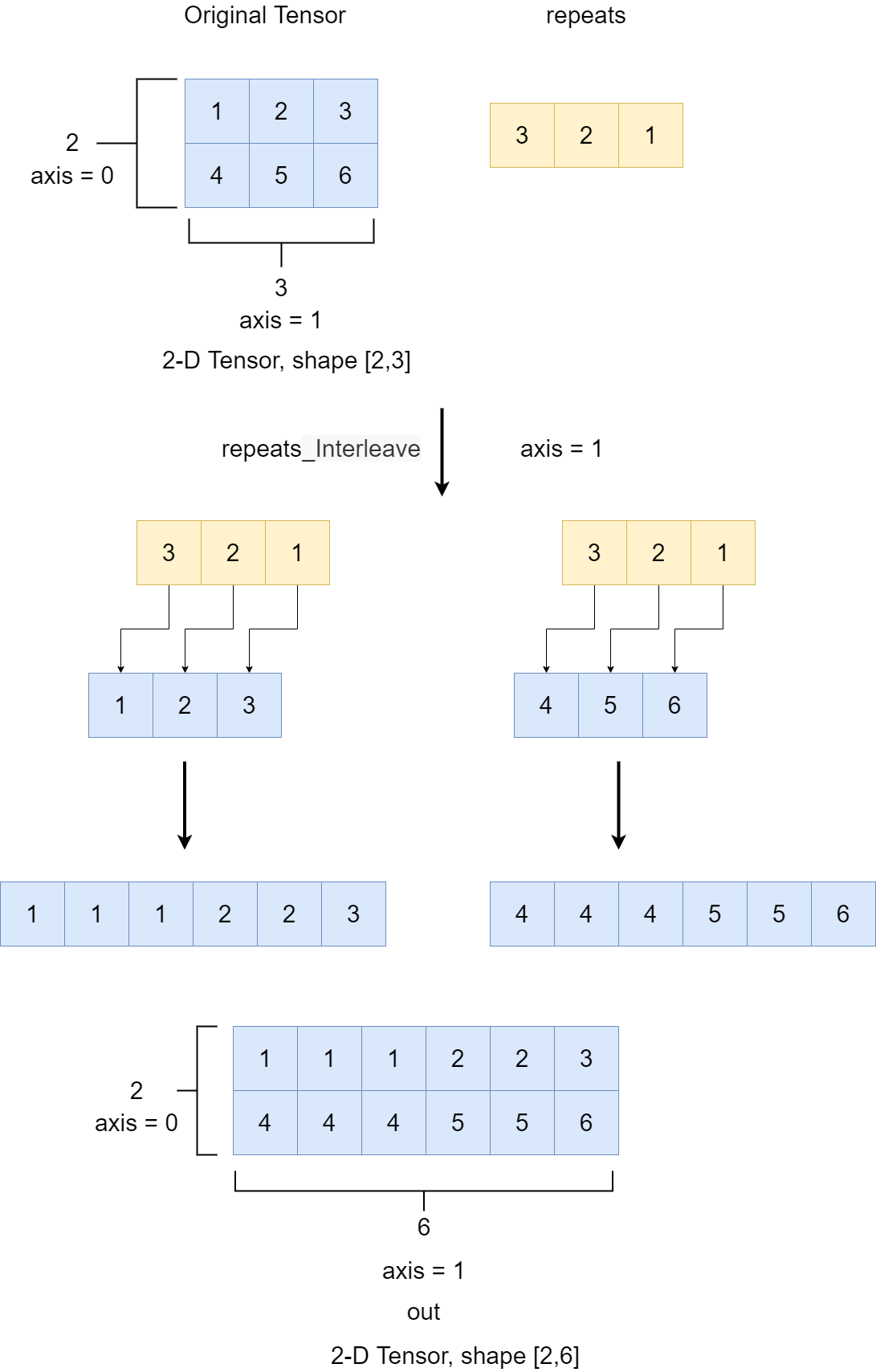
Note
Alias Support: The parameter name
inputcan be used as an alias forx, anddimcan be used as an alias foraxis. For example,repeat_interleave(input=tensor_x, dim=1, ...)is equivalent torepeat_interleave(x=tensor_x, axis=1, ...).- Parameters
-
x (Tensor) – The input Tensor to be operated. The data of
xcan be one of float32, float64, int32, int64. alias:input.repeats (Tensor|int) – The number of repetitions for each element. repeats is broadcasted to fit the shape of the given axis.
axis (int|None, optional) – The dimension in which we manipulate. Default: None, the output tensor is flatten. alias:
dim.name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
output_size (int, optional) – Total output size for the given axis (e.g. sum of repeats). If given, it will avoid stream synchronization needed to calculate output shape of the tensor.
- Returns
-
Tensor, A Tensor with same data type as
x.
Examples
>>> import paddle >>> x = paddle.to_tensor([[1, 2, 3], [4, 5, 6]]) >>> repeats = paddle.to_tensor([3, 2, 1], dtype='int32') >>> out = paddle.repeat_interleave(x, repeats, 1) >>> print(out) Tensor(shape=[2, 6], dtype=int64, place=Place(cpu), stop_gradient=True, [[1, 1, 1, 2, 2, 3], [4, 4, 4, 5, 5, 6]]) >>> out = paddle.repeat_interleave(x, 2, 0) >>> print(out) Tensor(shape=[4, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[1, 2, 3], [1, 2, 3], [4, 5, 6], [4, 5, 6]]) >>> out = paddle.repeat_interleave(x, 2, None) >>> print(out) Tensor(shape=[12], dtype=int64, place=Place(cpu), stop_gradient=True, [1, 1, 2, 2, 3, 3, 4, 4, 5, 5, 6, 6])
- property requires_grad : bool
-
Whether this Tensor requires gradient computation.
This is a convenience property that returns the opposite of stop_gradient. Setting requires_grad=True is equivalent to setting stop_gradient=False.
Examples
>>> import paddle >>> x = paddle.randn([2, 3]) >>> print(x.requires_grad) # False by default >>> >>> x.requires_grad = False >>> print(x.stop_gradient) # True
-
reshape
(
shape: ShapeLike,
name: str | None = None
)
Tensor
reshape¶
-
Changes the shape of
xwithout changing its data.Note that the output Tensor will share data with origin Tensor and doesn’t have a Tensor copy in
dygraphmode. If you want to use the Tensor copy version, please use Tensor.clone likereshape_clone_x = x.reshape([-1]).clone().Some tricks exist when specifying the target shape.
-
-1 means the value of this dimension is inferred from the total element number of x and remaining dimensions. Thus one and only one dimension can be set -1.
-
0 means the actual dimension value is going to be copied from the corresponding dimension of x. The index of 0s in shape can not exceed the dimension of x.
Here are some examples to explain it.
-
Given a 3-D tensor x with a shape [2, 4, 6], and the target shape is [6, 8], the reshape operator will transform x into a 2-D tensor with shape [6, 8] and leaving x’s data unchanged.
-
Given a 3-D tensor x with a shape [2, 4, 6], and the target shape specified is [2, 3, -1, 2], the reshape operator will transform x into a 4-D tensor with shape [2, 3, 4, 2] and leaving x’s data unchanged. In this case, one dimension of the target shape is set to -1, the value of this dimension is inferred from the total element number of x and remaining dimensions.
-
Given a 3-D tensor x with a shape [2, 4, 6], and the target shape is [-1, 0, 3, 2], the reshape operator will transform x into a 4-D tensor with shape [2, 4, 3, 2] and leaving x’s data unchanged. In this case, besides -1, 0 means the actual dimension value is going to be copied from the corresponding dimension of x.
The following figure illustrates the first example – a 3D tensor of shape [2, 4, 6] is transformed into a 2D tensor of shape [6, 8], during which the order and values of the elements in the tensor remain unchanged. The elements in the two subdiagrams correspond to each other, clearly demonstrating how the reshape API works.
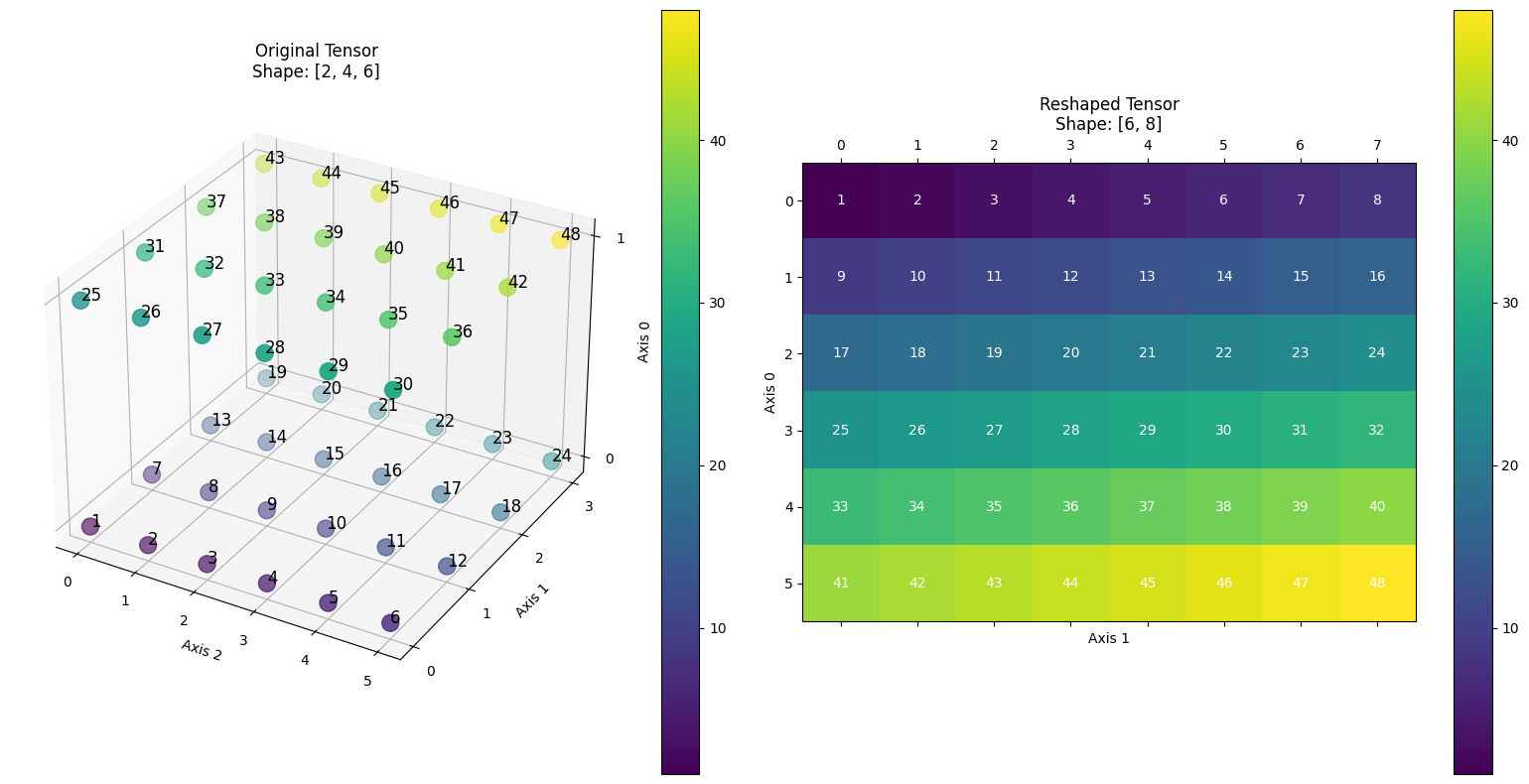
- Parameters
-
x (Tensor) – An N-D Tensor. The data type is
float16,float32,float64,int16,int32,int64,int8,uint8,complex64,complex128,bfloat16orbool.shape (list|tuple|Tensor) – Define the target shape. At most one dimension of the target shape can be -1. The data type is
int32. Ifshapeis a list or tuple, each element of it should be integer or Tensor with shape []. Ifshapeis a Tensor, it should be an 1-D Tensor .name (str, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, A reshaped Tensor with the same data type as
x.
Examples
>>> import paddle >>> x = paddle.rand([2, 4, 6], dtype="float32") >>> positive_four = paddle.full([1], 4, "int32") >>> out = paddle.reshape(x, [-1, 0, 3, 2]) >>> print(out.shape) [2, 4, 3, 2] >>> out = paddle.reshape(x, shape=[positive_four, 12]) >>> print(out.shape) [4, 12] >>> shape_tensor = paddle.to_tensor([8, 6], dtype=paddle.int32) >>> out = paddle.reshape(x, shape=shape_tensor) >>> print(out.shape) [8, 6] >>> # out shares data with x in dygraph mode >>> x[0, 0, 0] = 10. >>> print(out[0, 0]) Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 10.)
-
-
reshape_
(
shape: ShapeLike,
name: str | None = None
)
Tensor
reshape_¶
-
Inplace version of
reshapeAPI, the output Tensor will be inplaced with inputx. Please refer to api_paddle_tensor_reshape.
-
resize_
(
shape: Sequence[int],
fill_zero: bool = False,
name: str | None = None
)
paddle.Tensor
resize_¶
-
Resize
xwith specifiedshape.- Parameters
-
x (Tensor) – An arbitrary Tensor. The data type supports
bfloat16,float16,float32,float64,bool,int8,int16,int32,int64,uint8,complex64orcomplex128.shape (list|tuple) – Define the target shape. Each element of it should be integer.
fill_zero (bool, optional) – If the size of specified
shapeis greater than the original Tensor size, the new Tensor will be filled with zero iffill_zerois True. Default: False, which means the filled value will be undetermined.name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, the resized Tensor.
Examples
>>> import paddle >>> x = paddle.to_tensor([1., 2., 3.]) >>> x.resize_([2, 1]) >>> print(x) Tensor(shape=[2, 1], dtype=float32, place=Place(cpu), stop_gradient=True, [[1.], [2.]]) >>> x = paddle.to_tensor([1., 2., 3.]) >>> x.resize_([2, 3], fill_zero=True) >>> print(x) Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True, [[1., 2., 3.], [0., 0., 0.]])
-
reverse
(
axis: Sequence[int] | int,
name: str | None = None
)
Tensor
reverse¶
-
Reverse the order of a n-D tensor along given axis in axis.
The image below illustrates how
flipworks.
- Parameters
-
x (Tensor) – A Tensor with shape \([N_1, N_2,..., N_k]\) . The data type of the input Tensor x should be float32, float64, int32, int64, bool.
axis (list|tuple|int) – The axis(axes) to flip on. Negative indices for indexing from the end are accepted.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, Tensor or DenseTensor calculated by flip layer. The data type is same with input x.
Examples
>>> >>> import paddle >>> image_shape=(3, 2, 2) >>> img = paddle.arange(image_shape[0] * image_shape[1] * image_shape[2]).reshape(image_shape) >>> tmp = paddle.flip(img, [0,1]) >>> print(tmp) Tensor(shape=[3, 2, 2], dtype=int64, place=Place(cpu), stop_gradient=True, [[[10, 11], [8 , 9 ]], [[6 , 7 ], [4 , 5 ]], [[2 , 3 ], [0 , 1 ]]]) >>> out = paddle.flip(tmp,-1) >>> print(out) Tensor(shape=[3, 2, 2], dtype=int64, place=Place(cpu), stop_gradient=True, [[[11, 10], [9 , 8 ]], [[7 , 6 ], [5 , 4 ]], [[3 , 2 ], [1 , 0 ]]])
-
roll
(
)
roll¶
-
C++ interface function for roll.
-
rot90
(
k: int = 1,
axes: Sequence[int] = [0, 1],
name: str | None = None
)
Tensor
rot90¶
-
Rotate a n-D tensor by 90 degrees. The rotation direction and times are specified by axes and the absolute value of k. Rotation direction is from axes[0] towards axes[1] if k > 0, and from axes[1] towards axes[0] for k < 0.
- Parameters
-
x (Tensor) – The input Tensor. The data type of the input Tensor x should be float16, float32, float64, int32, int64, bool. float16 is only supported on gpu.
k (int, optional) – Direction and number of times to rotate, default value: 1.
axes (list|tuple, optional) – Axes to rotate, dimension must be 2. default value: [0, 1].
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name .
- Returns
-
Tensor, Tensor or DenseTensor calculated by rot90 layer. The data type is same with input x.
Examples
>>> import paddle >>> data = paddle.arange(4) >>> data = paddle.reshape(data, (2, 2)) >>> print(data.numpy()) [[0 1] [2 3]] >>> y = paddle.rot90(data, 1, [0, 1]) >>> print(y.numpy()) [[1 3] [0 2]] >>> y= paddle.rot90(data, -1, [0, 1]) >>> print(y.numpy()) [[2 0] [3 1]] >>> data2 = paddle.arange(8) >>> data2 = paddle.reshape(data2, (2,2,2)) >>> print(data2.numpy()) [[[0 1] [2 3]] [[4 5] [6 7]]] >>> y = paddle.rot90(data2, 1, [1, 2]) >>> print(y.numpy()) [[[1 3] [0 2]] [[5 7] [4 6]]]
-
round
(
decimals: int = 0,
name: str | None = None
)
Tensor
round¶
-
Round the values in the input to the nearest integer value.
input: x.shape = [4] x.data = [1.2, -0.9, 3.4, 0.9] output: out.shape = [4] out.data = [1., -1., 3., 1.]
- Parameters
-
x (Tensor) – Input of Round operator, an N-D Tensor, with data type bfloat16, int32, int64, float32, float64, float16, complex64 or complex128.
decimals (int) – Rounded decimal place (default: 0).
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor. Output of Round operator, a Tensor with shape same as input.
Examples
>>> import paddle >>> x = paddle.to_tensor([-0.5, -0.2, 0.6, 1.5]) >>> out = paddle.round(x) >>> print(out) Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [-0., -0., 1., 2.])
-
round_
(
decimals=0,
name=None
)
round_¶
-
Inplace version of
roundAPI, the output Tensor will be inplaced with inputx. Please refer to round.
-
rsqrt
(
)
rsqrt¶
-
C++ interface function for rsqrt.
-
rsqrt_
(
name=None
)
rsqrt_¶
-
Inplace version of
rsqrtAPI, the output Tensor will be inplaced with inputx. Please refer to rsqrt.
-
scale
(
scale: float | Tensor = 1.0,
bias: float = 0.0,
bias_after_scale: bool = True,
act: str | None = None,
name: str | None = None
)
Tensor
scale¶
-
Scale operator.
Putting scale and bias to the input Tensor as following:
bias_after_scaleis True:\[Out=scale*X+bias\]bias_after_scaleis False:\[Out=scale*(X+bias)\]- Parameters
-
x (Tensor) – Input N-D Tensor of scale operator. Data type can be bfloat16, float16, float32, float64, int8, int16, int32, int64, uint8, complex64, complex128.
scale (float|Tensor) – The scale factor of the input, it should be a float number or a 0-D Tensor with shape [] and data type as float32.
bias (float) – The bias to be put on the input.
bias_after_scale (bool) – Apply bias addition after or before scaling. It is useful for numeric stability in some circumstances.
act (str|None, optional) – Activation applied to the output such as tanh, softmax, sigmoid, relu.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Output Tensor of scale operator, with shape and data type same as input.
- Return type
-
Tensor
Examples
>>> # scale as a float32 number >>> import paddle >>> data = paddle.arange(6).astype("float32").reshape([2, 3]) >>> print(data) Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True, [[0., 1., 2.], [3., 4., 5.]]) >>> res = paddle.scale(data, scale=2.0, bias=1.0) >>> print(res) Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True, [[1. , 3. , 5. ], [7. , 9. , 11.]])
>>> # scale with parameter scale as a Tensor >>> import paddle >>> data = paddle.arange(6).astype("float32").reshape([2, 3]) >>> print(data) Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True, [[0., 1., 2.], [3., 4., 5.]]) >>> factor = paddle.to_tensor([2], dtype='float32') >>> res = paddle.scale(data, scale=factor, bias=1.0) >>> print(res) Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True, [[1. , 3. , 5. ], [7. , 9. , 11.]])
-
scale_
(
scale: float = 1.0,
bias: float = 0.0,
bias_after_scale: bool = True,
act: str | None = None,
name: str | None = None
)
Tensor
scale_¶
-
Inplace version of
scaleAPI, the output Tensor will be inplaced with inputx. Please refer to scale.
-
scatter
(
index: Tensor,
updates: Tensor,
overwrite: bool = True,
name: str | None = None
)
Tensor
scatter¶
-
Scatter Layer Output is obtained by updating the input on selected indices based on updates.
As shown in the figure, when
overwriteis set toTrue, the output for the same index is updated in overwrite mode, wherex[index[i]]is directly replaced withupdate[i]sequentially; Whenoverwriteis set toFalse, the output for the same index is updated in accumulation mode. In this mode,x[index[i]]is first initialized with elements set to 0. Then,update[i]is sequentially added tox[index[i]]to produce the output.
>>> import paddle >>> #input: >>> x = paddle.to_tensor([[1, 1], [2, 2], [3, 3]], dtype='float32') >>> index = paddle.to_tensor([2, 1, 0, 1], dtype='int64') >>> # shape of updates should be the same as x >>> # shape of updates with dim > 1 should be the same as input >>> updates = paddle.to_tensor([[1, 1], [2, 2], [3, 3], [4, 4]], dtype='float32') >>> overwrite = False >>> # calculation: >>> if not overwrite: ... for i in range(len(index)): ... x[index[i]] = paddle.zeros([2]) >>> for i in range(len(index)): ... if (overwrite): ... x[index[i]] = updates[i] ... else: ... x[index[i]] += updates[i] >>> # output: >>> out = paddle.to_tensor([[3, 3], [6, 6], [1, 1]]) >>> print(out.shape) [3, 2]
NOTICE: The order in which updates are applied is nondeterministic, so the output will be nondeterministic if index contains duplicates.
- Parameters
-
x (Tensor) – The input N-D Tensor with ndim>=1. Data type can be float32, float64.
index (Tensor) – The index is a 1-D or 0-D Tensor. Data type can be int32, int64. The length of index cannot exceed updates’s length, and the value in index cannot exceed input’s length.
updates (Tensor) – Update input with updates parameter based on index. When the index is a 1-D tensor, the updates shape should be the same as input, and dim value with dim > 1 should be the same as input. When the index is a 0-D tensor, the updates should be a (N-1)-D tensor, the ith dim of the updates should be equal with the (i+1)th dim of the input.
overwrite (bool, optional) – The mode that updating the output when there are same indices.If True, use the overwrite mode to update the output of the same index,if False, use the accumulate mode to update the output of the same index. Default value is True.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name .
- Returns
-
Tensor, The output is a Tensor with the same shape as x.
Examples
>>> import paddle >>> x = paddle.to_tensor([[1, 1], [2, 2], [3, 3]], dtype='float32') >>> index = paddle.to_tensor([2, 1, 0, 1], dtype='int64') >>> updates = paddle.to_tensor([[1, 1], [2, 2], [3, 3], [4, 4]], dtype='float32') >>> output1 = paddle.scatter(x, index, updates, overwrite=False) >>> print(output1) Tensor(shape=[3, 2], dtype=float32, place=Place(cpu), stop_gradient=True, [[3., 3.], [6., 6.], [1., 1.]]) >>> output2 = paddle.scatter(x, index, updates, overwrite=True) >>> # CPU device: >>> # [[3., 3.], >>> # [4., 4.], >>> # [1., 1.]] >>> # GPU device maybe have two results because of the repeated numbers in index >>> # result 1: >>> # [[3., 3.], >>> # [4., 4.], >>> # [1., 1.]] >>> # result 2: >>> # [[3., 3.], >>> # [2., 2.], >>> # [1., 1.]]
-
scatter_
(
index: Tensor,
updates: Tensor,
overwrite: bool = True,
name: str | None = None
)
Tensor
scatter_¶
-
Inplace version of
scatterAPI, the output Tensor will be inplaced with inputx. Please refer to api_paddle_tensor_scatter.
-
scatter_add
(
dim: int,
index: Tensor,
src: Tensor
)
Tensor
scatter_add¶
-
Scatter the values of the source tensor to the target tensor according to the given indices, and perform a add operation along the designated axis.
- Parameters
-
input (Tensor) – The Input Tensor. Supported data types are bfloat16, float16, float32, float64, int32, int64, uint8.
dim (int) – The axis to scatter 1d slices along.
index (Tensor) – Indices to scatter along each 1d slice of input. This must match the dimension of input, Supported data type are int32 and int64.
src (Tensor) – The value element(s) to scatter. The data types should be same as input.
- Returns
-
Tensor, The indexed element, same dtype with input
Examples
>>> import paddle >>> x = paddle.to_tensor([[10, 20, 30], [40, 50, 60]]) >>> indices = paddle.zeros((2,3)).astype("int32") >>> values = paddle.to_tensor([[1, 2, 3],[4, 5, 6]]).astype(x.dtype) >>> result = paddle.scatter_add(x, 0, indices, values) >>> print(result) Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[15, 27, 39], [40, 50, 60]])
-
scatter_add_
(
dim: int,
index: Tensor,
src: Tensor
)
Tensor
scatter_add_¶
-
Inplace version of
scatter_addAPI, the output Tensor will be inplaced with inputinput. Please refer to scatter_add.
-
scatter_nd
(
updates: Tensor,
shape: ShapeLike,
name: str | None = None
)
Tensor
scatter_nd¶
-
Scatter_nd Layer
Output is obtained by scattering the
updatesin a new tensor according toindex. This op is similar toscatter_nd_add, except the tensor ofshapeis zero-initialized. Correspondingly,scatter_nd(index, updates, shape)is equal toscatter_nd_add(paddle.zeros(shape, updates.dtype), index, updates). Ifindexhas repeated elements, then the corresponding updates are accumulated. Because of the numerical approximation issues, the different order of repeated elements inindexmay cause different results. The specific calculation method can be seenscatter_nd_add. This op is the inverse of thegather_ndop.- Parameters
-
index (Tensor) – The index input with ndim >= 1 and index.shape[-1] <= len(shape). Its dtype should be int32 or int64 as it is used as indexes.
updates (Tensor) – The updated value of scatter_nd op. Its dtype should be float32, float64. It must have the shape index.shape[:-1] + shape[index.shape[-1]:]
shape (tuple|list|Tensor) – Shape of output tensor.
name (str|None, optional) – The output Tensor name. If set None, the layer will be named automatically.
- Returns
-
output (Tensor), The output is a tensor with the same type as
updates.
Examples
>>> import paddle >>> index = paddle.to_tensor([[1, 1], ... [0, 1], ... [1, 3]], dtype="int64") >>> updates = paddle.rand(shape=[3, 9, 10], dtype='float32') >>> shape = [3, 5, 9, 10] >>> output = paddle.scatter_nd(index, updates, shape)
-
scatter_nd_add
(
index: Tensor,
updates: Tensor,
name: str | None = None
)
Tensor
scatter_nd_add¶
-
Output is obtained by applying sparse addition to a single value or slice in a Tensor.
xis a Tensor with ndim \(R\) andindexis a Tensor with ndim \(K\) . Thus,indexhas shape \([i_0, i_1, ..., i_{K-2}, Q]\) where \(Q \leq R\) .updatesis a Tensor with ndim \(K - 1 + R - Q\) and its shape is \(index.shape[:-1] + x.shape[index.shape[-1]:]\) .According to the \([i_0, i_1, ..., i_{K-2}]\) of
index, add the correspondingupdatesslice to thexslice which is obtained by the last one dimension ofindex.Given: * Case 1: x = [0, 1, 2, 3, 4, 5] index = [[1], [2], [3], [1]] updates = [9, 10, 11, 12] we get: output = [0, 22, 12, 14, 4, 5] * Case 2: x = [[65, 17], [-14, -25]] index = [[], []] updates = [[[-1, -2], [1, 2]], [[3, 4], [-3, -4]]] x.shape = (2, 2) index.shape = (2, 0) updates.shape = (2, 2, 2) we get: output = [[67, 19], [-16, -27]]- Parameters
-
x (Tensor) – The x input. Its dtype should be int32, int64, float32, float64.
index (Tensor) – The index input with ndim > 1 and index.shape[-1] <= x.ndim. Its dtype should be int32 or int64 as it is used as indexes.
updates (Tensor) – The updated value of scatter_nd_add op, and it must have the same dtype as x. It must have the shape index.shape[:-1] + x.shape[index.shape[-1]:].
name (str|None, optional) – The output tensor name. If set None, the layer will be named automatically.
- Returns
-
output (Tensor), The output is a tensor with the same shape and dtype as x.
Examples
>>> import paddle >>> x = paddle.rand(shape=[3, 5, 9, 10], dtype='float32') >>> updates = paddle.rand(shape=[3, 9, 10], dtype='float32') >>> index = paddle.to_tensor([[1, 1], ... [0, 1], ... [1, 3]], dtype='int64') >>> output = paddle.scatter_nd_add(x, index, updates) >>> print(output.shape) [3, 5, 9, 10]
-
scatter_reduce
(
dim: int,
index: Tensor,
src: Tensor,
reduce: Literal['sum', 'prod', 'mean', 'amin', 'amax'],
*,
include_self: bool = True
)
Tensor
scatter_reduce¶
-
Scatter the values of the source tensor to the target tensor according to the given indices, and perform a reduction operation along the designated axis.
- Parameters
-
input (Tensor) – The Input Tensor. Supported data types are bfloat16, float16, float32, float64, int32, int64, uint8.
dim (int) – The axis to scatter 1d slices along.
index (Tensor) – Indices to scatter along each 1d slice of input. This must match the dimension of input, Supported data type are int32 and int64.
src (Tensor) – The value element(s) to scatter. The data types should be same as input.
reduce (str) – The reduce operation, support ‘sum’, ‘prod’, ‘mean’, ‘amin’, ‘amax’.
include_self (bool, optional) – whether to reduce with the elements of input, default is ‘True’.
- Returns
-
Tensor, The indexed element, same dtype with input
Examples
>>> import paddle >>> x = paddle.to_tensor([[10, 20, 30], [40, 50, 60]]) >>> indices = paddle.zeros((2,3)).astype("int32") >>> values = paddle.to_tensor([[1, 2, 3],[4, 5, 6]]).astype(x.dtype) >>> result = paddle.scatter_reduce(x, 0, indices, values, "sum", include_self=True) >>> print(result) Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[15, 27, 39], [40, 50, 60]]) >>> result = paddle.scatter_reduce(x, 0, indices, values, "prod", include_self=True) >>> print(result) Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[40 , 200, 540], [40 , 50 , 60 ]]) >>> result = paddle.scatter_reduce(x, 0, indices, values, "mean", include_self=True) >>> print(result) Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[5 , 9 , 13], [40, 50, 60]])
-
select_scatter
(
values: Tensor,
axis: int,
index: int,
name: str | None = None
)
Tensor
select_scatter¶
-
Embeds the values of the values tensor into x at the given index of axis.
- Parameters
-
x (Tensor) – The Destination Tensor. Supported data types are bool, float16, float32, float64, uint8, int8, int16, int32, int64, bfloat16, complex64, complex128.
values (Tensor) – The tensor to embed into x. Supported data types are bool, float16, float32, float64, uint8, int8, int16, int32, int64, bfloat16, complex64, complex128.
axis (int) – the dimension to insert the slice into.
index (int) – the index to select with.
name (str|None, optional) – Name for the operation (optional, default is None).
- Returns
-
Tensor, same dtype and shape with x
Examples
>>> import paddle >>> x = paddle.zeros((2,3,4)).astype("float32") >>> values = paddle.ones((2,4)).astype("float32") >>> res = paddle.select_scatter(x,values,1,1) >>> print(res) Tensor(shape=[2, 3, 4], dtype=float32, place=Place(cpu), stop_gradient=True, [[[0., 0., 0., 0.], [1., 1., 1., 1.], [0., 0., 0., 0.]], [[0., 0., 0., 0.], [1., 1., 1., 1.], [0., 0., 0., 0.]]])
-
set_
(
source: paddle.Tensor | None = None,
shape: Sequence[int] | None = None,
stride: Sequence[int] | None = None,
offset: int = 0,
name: str | None = None
)
paddle.Tensor
set_¶
-
set x with specified source Tensor’s underlying storage, shape, stride and offset.
Note that the
xwill share the same data withsourceTensor.- Parameters
-
x (Tensor) – An arbitrary Tensor. The data type supports
bfloat16,float16,float32,float64,bool,int8,int16,int32,int64,uint8,complex64orcomplex128.source (Tensor|None, optional) – Define the target Tensor to use. The data type supports bfloat16,
float16,float32,float64,bool,int8,int16,int32,int64,uint8,complex64orcomplex128. Default: None, which means to setxwith an empty source tensor.shape (list|tuple|None, optional) – Define the target shape. Each element of it should be integer. Default: None, which means it will use the specified
source’s shape as default value.stride (list|tuple|None, optional) – Define the target stride. Each element of it should be integer. Default: None, and when
shapeis also None, it will use the specifiedsource’s stride as default value; whenshapeis specified, it will use the default stride corresponding to the specifiedshape.offset (int, optional) – Define the target offset from x’s holder. Default: 0.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, the Tensor with the same data type as
x.
Examples
>>> import paddle >>> src = paddle.to_tensor([[11., 22., 33.]]) >>> src2 = paddle.to_tensor([11., 22., 33., 44., 55., 66.]) >>> x = paddle.to_tensor([1., 2., 3., 4., 5.]) >>> x.set_() >>> print(x) Tensor(shape=[0], dtype=float32, place=Place(cpu), stop_gradient=True, []) >>> x = paddle.to_tensor([1., 2., 3., 4., 5.]) >>> x.set_(src) >>> print(x) Tensor(shape=[1, 3], dtype=float32, place=Place(cpu), stop_gradient=True, [[11., 22., 33.]]) >>> print(x._is_shared_buffer_with(src)) True >>> x = paddle.to_tensor([1., 2., 3., 4., 5.]) >>> x.set_(src, shape=[2, 1]) >>> print(x) Tensor(shape=[2, 1], dtype=float32, place=Place(cpu), stop_gradient=True, [[11.], [22.]]) >>> x = paddle.to_tensor([1., 2., 3., 4., 5.]) >>> x.set_(src2, shape=[3], stride=[2]) >>> print(x) Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True, [11., 33., 55.]) >>> x = paddle.to_tensor([1., 2., 3., 4., 5.]) >>> x.set_(src2, shape=[5], offset=4) >>> print(x) Tensor(shape=[5], dtype=float32, place=Place(cpu), stop_gradient=True, [22., 33., 44., 55., 66.])
-
sgn
(
name: str | None = None
)
Tensor
sgn¶
-
For complex tensor, this API returns a new tensor whose elements have the same angles as the corresponding elements of input and absolute values of one. For other float dtype tensor, this API returns sign of every element in x: 1 for positive, -1 for negative and 0 for zero, same as paddle.sign.
- Parameters
-
x (Tensor) – The input tensor, which data type should be float16, float32, float64, complex64, complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
A sign Tensor for real input, or normalized Tensor for complex input, shape and data type are same as input.
- Return type
-
Tensor
Examples
>>> import paddle >>> x = paddle.to_tensor([[3 + 4j, 7 - 24j, 0, 1 + 2j], [6 + 8j, 3, 0, -2]]) >>> paddle.sgn(x) Tensor(shape=[2, 4], dtype=complex64, place=Place(cpu), stop_gradient=True, [[ (0.6000000238418579+0.800000011920929j), (0.2800000011920929-0.9599999785423279j), 0j , (0.4472135901451111+0.8944271802902222j)], [ (0.6000000238418579+0.800000011920929j), (1+0j) , 0j , (-1+0j) ]])
-
shard_index
(
index_num: int,
nshards: int,
shard_id: int,
ignore_value: int = -1
)
Tensor
shard_index¶
-
Reset the values of input according to the shard it belongs to. Every value in input must be a non-negative integer, and the parameter index_num represents the integer above the maximum value of input. Thus, all values in input must be in the range [0, index_num) and each value can be regarded as the offset to the beginning of the range. The range is further split into multiple shards. Specifically, we first compute the shard_size according to the following formula, which represents the number of integers each shard can hold. So for the i’th shard, it can hold values in the range [i*shard_size, (i+1)*shard_size).
shard_size = (index_num + nshards - 1) // nshards
For each value v in input, we reset it to a new value according to the following formula:
v = v - shard_id * shard_size if shard_id * shard_size <= v < (shard_id+1) * shard_size else ignore_value
That is, the value v is set to the new offset within the range represented by the shard shard_id if it in the range. Otherwise, we reset it to be ignore_value.
As shown below, a
[2, 1]2D tensor is updated with theshard_indexoperation. Givenindex_num = 20,nshards = 2, andshard_id = 0, the shard size isshard_size = (20 + 2 - 1) // 2 = 10. For each label element: if its value is in [0, 10), it’s adjusted to its offset; e.g., 1 becomes 1 - 0 * 10 = 1. Otherwise, it’s set to the default ignore_value of -1, like 16 becoming -1.
- Parameters
-
input (Tensor) – Input tensor with data type int64 or int32. It’s last dimension must be 1.
index_num (int) – An integer represents the integer above the maximum value of input.
nshards (int) – The number of shards.
shard_id (int) – The index of the current shard.
ignore_value (int, optional) – An integer value out of sharded index range. The default value is -1.
- Returns
-
Tensor.
Examples
>>> import paddle >>> label = paddle.to_tensor([[16], [1]], "int64") >>> shard_label = paddle.shard_index(input=label, ... index_num=20, ... nshards=2, ... shard_id=0) >>> print(shard_label.numpy()) [[-1] [ 1]]
-
sigmoid
(
)
sigmoid¶
-
C++ interface function for sigmoid.
-
sigmoid_
(
name=None
)
sigmoid_¶
-
Inplace version of
sigmoidAPI, the output Tensor will be inplaced with inputx. Please refer to api_paddle_sigmoid.
-
sign
(
)
sign¶
-
C++ interface function for sign.
-
signbit
(
name: str | None = None
)
Tensor
signbit¶
-
Tests if each element of input has its sign bit set or not.
- Parameters
-
x (Tensor) – The input Tensor. Must be one of the following types: float16, float32, float64, bfloat16, uint8, int8, int16, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None).For more information, please refer to api_guide_Name.
- Returns
-
The output Tensor. The sign bit of the corresponding element of the input tensor, True means negative, False means positive.
- Return type
-
out (Tensor)
Examples
>>> import paddle >>> paddle.set_device('cpu') >>> x = paddle.to_tensor([-0., 1.1, -2.1, 0., 2.5], dtype='float32') >>> res = paddle.signbit(x) >>> print(res) Tensor(shape=[5], dtype=bool, place=Place(cpu), stop_gradient=True, [True, False, True, False, False])
>>> import paddle >>> paddle.set_device('cpu') >>> x = paddle.to_tensor([-5, -2, 3], dtype='int32') >>> res = paddle.signbit(x) >>> print(res) Tensor(shape=[3], dtype=bool, place=Place(cpu), stop_gradient=True, [True , True , False])
-
sin
(
)
sin¶
-
C++ interface function for sin.
-
sin_
(
name=None
)
sin_¶
-
Inplace version of
sinAPI, the output Tensor will be inplaced with inputx. Please refer to sin.
-
sinc
(
name: str | None = None
)
Tensor
sinc¶
-
Calculate the normalized sinc of
xelementwise.\[\begin{split}out_i = \left\{ \begin{aligned} &1 & \text{ if $x_i = 0$} \\ &\frac{\sin(\pi x_i)}{\pi x_i} & \text{ otherwise} \end{aligned} \right.\end{split}\]- Parameters
-
x (Tensor) – The input Tensor. Must be one of the following types: bfloat16, float16, float32, float64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
out (Tensor), The Tensor of elementwise-computed normalized sinc result.
Examples
>>> import paddle >>> paddle.set_device('cpu') >>> paddle.seed(100) >>> x = paddle.rand([2,3], dtype='float32') >>> res = paddle.sinc(x) >>> print(res) Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True, [[0.56691176, 0.93089867, 0.99977750], [0.61639023, 0.79618412, 0.89171958]])
-
sinc_
(
name: str | None = None
)
Tensor
sinc_¶
-
Inplace version of
sincAPI, the output Tensor will be inplaced with inputx. Please refer to sinc.
-
sinh
(
name: str | None = None
)
Tensor
sinh¶
-
Sinh Activation Operator.
\[out = sinh(x)\]- Parameters
-
x (Tensor) – Input of Sinh operator, an N-D Tensor, with data type float32, float64, float16, bfloat16, uint8, int8, int16, int32, int64, complex64 or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
- Tensor. Output of Sinh operator, a Tensor with shape same as input
-
(integer types are autocasted into float32).
Examples
>>> import paddle >>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3]) >>> out = paddle.sinh(x) >>> print(out) Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [-0.41075233, -0.20133601, 0.10016675, 0.30452031])
-
sinh_
(
name=None
)
sinh_¶
-
Inplace version of
sinhAPI, the output Tensor will be inplaced with inputx. Please refer to sinh.
-
slice
(
axes: Sequence[int | Tensor],
starts: Sequence[int | Tensor] | Tensor,
ends: Sequence[int | Tensor] | Tensor
)
Tensor
slice¶
-
This operator produces a slice of
inputalong multiple axes. Similar to numpy: https://docs.scipy.org/doc/numpy/reference/arrays.indexing.html Slice usesaxes,startsandendsattributes to specify the start and end dimension for each axis in the list of axes and Slice uses this information to slice the input data tensor. If a negative value is passed tostartsorendssuch as \(-i\), it represents the reverse position of the axis \(i-1\) (here 0 is the initial position). If the value passed tostartsorendsis greater than n (the number of elements in this dimension), it represents n. For slicing to the end of a dimension with unknown size, it is recommended to pass in INT_MAX. The size ofaxesmust be equal tostartsandends. Following examples will explain how slice works:Case1: Given: data = [ [1, 2, 3, 4], [5, 6, 7, 8], ] axes = [0, 1] starts = [1, 0] ends = [2, 3] Then: result = [ [5, 6, 7], ] Case2: Given: data = [ [1, 2, 3, 4], [5, 6, 7, 8], ] axes = [0, 1] starts = [0, 1] ends = [-1, 1000] # -1 denotes the reverse 0th position of dimension 0. Then: result = [ [2, 3, 4], ] # result = data[0:1, 1:4]The following figure illustrates the first case – a 2D tensor of shape [2, 4] is transformed into a 2D tensor of shape [1, 3] through a slicing operation.
- Parameters
-
input (Tensor) – A
Tensor. The data type isfloat16,float32,float64,int32orint64.axes (list|tuple) – The data type is
int32. Axes that starts and ends apply to .starts (list|tuple|Tensor) – The data type is
int32. Ifstartsis a list or tuple, each element of it should be integer or 0-D int Tensor with shape []. Ifstartsis an Tensor, it should be an 1-D Tensor. It represents starting indices of corresponding axis inaxes.ends (list|tuple|Tensor) – The data type is
int32. Ifendsis a list or tuple, each element of it should be integer or 0-D int Tensor with shape []. Ifendsis an Tensor, it should be an 1-D Tensor . It represents ending indices of corresponding axis inaxes.
- Returns
-
Tensor, A
Tensor. The data type is same asinput.
Examples
>>> import paddle >>> input = paddle.rand(shape=[4, 5, 6], dtype='float32') >>> # example 1: >>> # attr starts is a list which doesn't contain tensor. >>> axes = [0, 1, 2] >>> starts = [-3, 0, 2] >>> ends = [3, 2, 4] >>> sliced_1 = paddle.slice(input, axes=axes, starts=starts, ends=ends) >>> # sliced_1 is input[1:3, 0:2, 2:4]. >>> # example 2: >>> # attr starts is a list which contain tensor. >>> minus_3 = paddle.full([1], -3, "int32") >>> sliced_2 = paddle.slice(input, axes=axes, starts=[minus_3, 0, 2], ends=ends) >>> # sliced_2 is input[1:3, 0:2, 2:4].
-
slice_scatter
(
value: Tensor,
axes: Sequence[int],
starts: Sequence[int],
ends: Sequence[int],
strides: Sequence[int],
name: str | None = None
)
Tensor
slice_scatter¶
-
Embeds the value tensor into x along multiple axes. Returns a new tensor instead of a view. The size of axes must be equal to starts , ends and strides.
- Parameters
-
x (Tensor) – The input Tensor. Supported data types are bool, float16, float32, float64, uint8, int8, int16, int32, int64, bfloat16, complex64, complex128.
value (Tensor) – The tensor to embed into x. Supported data types are bool, float16, float32, float64, uint8, int8, int16, int32, int64, bfloat16, complex64, complex128.
axes (list|tuple) – the dimensions to insert the value.
starts (list|tuple) – the start indices of where to insert.
ends (list|tuple) – the stop indices of where to insert.
strides (list|tuple) – the steps for each insert.
name (str|None, optional) – Name for the operation (optional, default is None).
- Returns
-
Tensor, same dtype and shape with x
Examples
>>> import paddle >>> x = paddle.zeros((3, 9)) >>> value = paddle.ones((3, 2)) >>> res = paddle.slice_scatter(x, value, axes=[1], starts=[2], ends=[6], strides=[2]) >>> print(res) Tensor(shape=[3, 9], dtype=float32, place=Place(cpu), stop_gradient=True, [[0., 0., 1., 0., 1., 0., 0., 0., 0.], [0., 0., 1., 0., 1., 0., 0., 0., 0.], [0., 0., 1., 0., 1., 0., 0., 0., 0.]]) >>> # broadcast `value` got the same result >>> x = paddle.zeros((3, 9)) >>> value = paddle.ones((3, 1)) >>> res = paddle.slice_scatter(x, value, axes=[1], starts=[2], ends=[6], strides=[2]) >>> print(res) Tensor(shape=[3, 9], dtype=float32, place=Place(cpu), stop_gradient=True, [[0., 0., 1., 0., 1., 0., 0., 0., 0.], [0., 0., 1., 0., 1., 0., 0., 0., 0.], [0., 0., 1., 0., 1., 0., 0., 0., 0.]]) >>> # broadcast `value` along multiple axes >>> x = paddle.zeros((3, 3, 5)) >>> value = paddle.ones((1, 3, 1)) >>> res = paddle.slice_scatter(x, value, axes=[0, 2], starts=[1, 0], ends=[3, 4], strides=[1, 2]) >>> print(res) Tensor(shape=[3, 3, 5], dtype=float32, place=Place(cpu), stop_gradient=True, [[[0., 0., 0., 0., 0.], [0., 0., 0., 0., 0.], [0., 0., 0., 0., 0.]], [[1., 0., 1., 0., 0.], [1., 0., 1., 0., 0.], [1., 0., 1., 0., 0.]], [[1., 0., 1., 0., 0.], [1., 0., 1., 0., 0.], [1., 0., 1., 0., 0.]]])
-
softmax
(
dim: int | None = None,
dtype: DTypeLike | None = None,
*,
out: Tensor | None = None
)
Tensor
softmax¶
-
This operator implements the compat.softmax. The calculation process is as follows:
The dimension
dimofinputwill be permuted to the last.
2. Then
inputwill be logically flattened to a 2-D matrix. The matrix’s second dimension(row length) is the same as the dimensionaxisofinput, and the first dimension(column length) is the product of all other dimensions ofinput. For each row of the matrix, the softmax operator squashes the K-dimensional(K is the width of the matrix, which is also the size ofinput’s dimensiondim) vector of arbitrary real values to a K-dimensional vector of real values in the range [0, 1] that add up to 1.3. After the softmax operation is completed, the inverse operations of steps 1 and 2 are performed to restore the two-dimensional matrix to the same dimension as the
input.It computes the exponential of the given dimension and the sum of exponential values of all the other dimensions in the K-dimensional vector input. Then the ratio of the exponential of the given dimension and the sum of exponential values of all the other dimensions is the output of the softmax operator.
For each row \(i\) and each column \(j\) in the matrix, we have:
\[softmax[i, j] = \frac{\exp(input[i, j])}{\sum_j(exp(input[i, j])}\]Example:
Case 1: Input: input.shape = [2, 3, 4] input.data = [[[2.0, 3.0, 4.0, 5.0], [3.0, 4.0, 5.0, 6.0], [7.0, 8.0, 8.0, 9.0]], [[1.0, 2.0, 3.0, 4.0], [5.0, 6.0, 7.0, 8.0], [6.0, 7.0, 8.0, 9.0]]] Attrs: dim = -1 Output: out.shape = [2, 3, 4] out.data = [[[0.0320586 , 0.08714432, 0.23688282, 0.64391426], [0.0320586 , 0.08714432, 0.23688282, 0.64391426], [0.07232949, 0.19661193, 0.19661193, 0.53444665]], [[0.0320586 , 0.08714432, 0.23688282, 0.64391426], [0.0320586 , 0.08714432, 0.23688282, 0.64391426], [0.0320586 , 0.08714432, 0.23688282, 0.64391426]]] Case 2: Input: input.shape = [2, 3, 4] input.data = [[[2.0, 3.0, 4.0, 5.0], [3.0, 4.0, 5.0, 6.0], [7.0, 8.0, 8.0, 9.0]], [[1.0, 2.0, 3.0, 4.0], [5.0, 6.0, 7.0, 8.0], [6.0, 7.0, 8.0, 9.0]]] Attrs: dim = 1 Output: out.shape = [2, 3, 4] out.data = [[[0.00657326, 0.00657326, 0.01714783, 0.01714783], [0.01786798, 0.01786798, 0.04661262, 0.04661262], [0.97555875, 0.97555875, 0.93623955, 0.93623955]], [[0.00490169, 0.00490169, 0.00490169, 0.00490169], [0.26762315, 0.26762315, 0.26762315, 0.26762315], [0.72747516, 0.72747516, 0.72747516, 0.72747516]]]- Parameters
-
input (Tensor) – The input Tensor with data type bfloat16, float16, float32, float64.
dim (int, optional) – The dim along which to perform softmax calculations. It should be in range [-D, D), where D is the rank of
input. Ifdim< 0, it works the same way as \(dim + D\) . Default is None.dtype (str, optional) – The data type of the output tensor, can be bfloat16, float16, float32, float64.
out (Tensor, optional) – The output Tensor.
- Returns
-
A Tensor with the same shape and data type (use
dtypeif it is specified) as input.
Examples
>>> import paddle >>> x = paddle.to_tensor([[[2.0, 3.0, 4.0, 5.0], ... [3.0, 4.0, 5.0, 6.0], ... [7.0, 8.0, 8.0, 9.0]], ... [[1.0, 2.0, 3.0, 4.0], ... [5.0, 6.0, 7.0, 8.0], ... [6.0, 7.0, 8.0, 9.0]]],dtype='float32') >>> out1 = paddle.compat.softmax(x, -1) >>> out2 = paddle.compat.softmax(x, -1, dtype='float64') >>> #out1's data type is float32; out2's data type is float64 >>> #out1 and out2's value is as follows: >>> print(out1) >>> print(out2) Tensor(shape=[2, 3, 4], dtype=float32, place=Place(cpu), stop_gradient=True, [[[0.03205860, 0.08714432, 0.23688284, 0.64391428], [0.03205860, 0.08714432, 0.23688284, 0.64391428], [0.07232949, 0.19661194, 0.19661194, 0.53444666]], [[0.03205860, 0.08714432, 0.23688284, 0.64391428], [0.03205860, 0.08714432, 0.23688284, 0.64391428], [0.03205860, 0.08714432, 0.23688284, 0.64391428]]]) Tensor(shape=[2, 3, 4], dtype=float64, place=Place(cpu), stop_gradient=True, [[[0.03205860, 0.08714432, 0.23688282, 0.64391426], [0.03205860, 0.08714432, 0.23688282, 0.64391426], [0.07232949, 0.19661193, 0.19661193, 0.53444665]], [[0.03205860, 0.08714432, 0.23688282, 0.64391426], [0.03205860, 0.08714432, 0.23688282, 0.64391426], [0.03205860, 0.08714432, 0.23688282, 0.64391426]]])
-
solve
(
y: Tensor,
left: bool = True,
name: str | None = None
)
Tensor
solve¶
-
Computes the solution of a square system of linear equations with a unique solution for input ‘X’ and ‘Y’. Let \(X\) be a square matrix or a batch of square matrices, \(Y\) be a vector/matrix or a batch of vectors/matrices. When left is True, the equation should be:
\[Out = X^-1 * Y\]When left is False, the equation should be:
\[Out = Y * X^-1\]Specifically, this system of linear equations has one solution if and only if input ‘X’ is invertible.
- Parameters
-
x (Tensor) – A square matrix or a batch of square matrices. Its shape should be
[*, M, M], where*is zero or more batch dimensions. Its data type should be float32 or float64.y (Tensor) – A vector/matrix or a batch of vectors/matrices. Its shape should be
[*, M, K], where*is zero or more batch dimensions. Its data type should be float32 or float64.left (bool, optional) – Whether to solve the system \(X * Out = Y\) or \(Out * X = Y\). Default: True.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
The solution of a square system of linear equations with a unique solution for input ‘x’ and ‘y’. Its data type should be the same as that of x.
- Return type
-
Tensor
Examples
>>> # a square system of linear equations: >>> # 3*X0 + X1 = 9 >>> # X0 + 2*X1 = 8 >>> import paddle >>> x = paddle.to_tensor([[3, 1],[1, 2]], dtype="float64") >>> y = paddle.to_tensor([9, 8], dtype="float64") >>> out = paddle.linalg.solve(x, y) >>> print(out) Tensor(shape=[2], dtype=float64, place=Place(cpu), stop_gradient=True, [2., 3.])
-
sort
(
axis: int = -1,
descending: bool = False,
stable: bool = False,
name: str | None = None
)
Tensor
sort¶
-
Sorts the input along the given axis, and returns the sorted output tensor. The default sort algorithm is ascending, if you want the sort algorithm to be descending, you must set the
descendingas True.- Parameters
-
x (Tensor) – An input N-D Tensor with type float32, float64, int16, int32, int64, uint8.
axis (int, optional) – Axis to compute indices along. The effective range is [-R, R), where R is Rank(x). when axis<0, it works the same way as axis+R. Default is -1.
descending (bool, optional) – Descending is a flag, if set to true, algorithm will sort by descending order, else sort by ascending order. Default is false.
stable (bool, optional) – Whether to use stable sorting algorithm or not. When using stable sorting algorithm, the order of equivalent elements will be preserved. Default is False.
name (str, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Returns
-
Tensor, sorted tensor(with the same shape and data type as
x).
Examples
>>> import paddle >>> x = paddle.to_tensor([[[5,8,9,5], ... [0,0,1,7], ... [6,9,2,4]], ... [[5,2,4,2], ... [4,7,7,9], ... [1,7,0,6]]], ... dtype='float32') >>> out1 = paddle.sort(x=x, axis=-1) >>> out2 = paddle.sort(x=x, axis=0) >>> out3 = paddle.sort(x=x, axis=1) >>> print(out1.numpy()) [[[5. 5. 8. 9.] [0. 0. 1. 7.] [2. 4. 6. 9.]] [[2. 2. 4. 5.] [4. 7. 7. 9.] [0. 1. 6. 7.]]] >>> print(out2.numpy()) [[[5. 2. 4. 2.] [0. 0. 1. 7.] [1. 7. 0. 4.]] [[5. 8. 9. 5.] [4. 7. 7. 9.] [6. 9. 2. 6.]]] >>> print(out3.numpy()) [[[0. 0. 1. 4.] [5. 8. 2. 5.] [6. 9. 9. 7.]] [[1. 2. 0. 2.] [4. 7. 4. 6.] [5. 7. 7. 9.]]]
-
split
(
num_or_sections: int | Sequence[int],
axis: int | Tensor = 0,
name: str | None = None
)
list[Tensor]
split¶
-
Split the input tensor into multiple sub-Tensors.
- Parameters
-
x (Tensor) – A N-D Tensor. The data type is bool, bfloat16, float16, float32, float64, uint8, int8, int32 or int64.
num_or_sections (int|list|tuple) – If
num_or_sectionsis an int, thennum_or_sectionsindicates the number of equal sized sub-Tensors that thexwill be divided into. Ifnum_or_sectionsis a list or tuple, the length of it indicates the number of sub-Tensors and the elements in it indicate the sizes of sub-Tensors’ dimension orderly. The length of the list must not be larger than thex‘s size of specifiedaxis.axis (int|Tensor, optional) – The axis along which to split, it can be a integer or a
0-D Tensorwith shape [] and data typeint32orint64. If :math::axis < 0, the axis to split along is \(rank(x) + axis\). Default is 0.name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name .
- Returns
-
list(Tensor), The list of segmented Tensors.
Examples
>>> import paddle >>> # x is a Tensor of shape [3, 9, 5] >>> x = paddle.rand([3, 9, 5]) >>> out0, out1, out2 = paddle.split(x, num_or_sections=3, axis=1) >>> print(out0.shape) [3, 3, 5] >>> print(out1.shape) [3, 3, 5] >>> print(out2.shape) [3, 3, 5] >>> out0, out1, out2 = paddle.split(x, num_or_sections=[2, 3, 4], axis=1) >>> print(out0.shape) [3, 2, 5] >>> print(out1.shape) [3, 3, 5] >>> print(out2.shape) [3, 4, 5] >>> out0, out1, out2 = paddle.split(x, num_or_sections=[2, 3, -1], axis=1) >>> print(out0.shape) [3, 2, 5] >>> print(out1.shape) [3, 3, 5] >>> print(out2.shape) [3, 4, 5] >>> # axis is negative, the real axis is (rank(x) + axis)=1 >>> out0, out1, out2 = paddle.split(x, num_or_sections=3, axis=-2) >>> print(out0.shape) [3, 3, 5] >>> print(out1.shape) [3, 3, 5] >>> print(out2.shape) [3, 3, 5]
-
sqrt
(
)
sqrt¶
-
C++ interface function for sqrt.
-
sqrt_
(
name=None
)
sqrt_¶
-
Inplace version of
sqrtAPI, the output Tensor will be inplaced with inputx. Please refer to sqrt.
-
square
(
name: str | None = None
)
Tensor
square¶
-
Square each elements of the inputs.
\[out = x^2\]- Parameters
-
x (Tensor) – Input of Square operator, an N-D Tensor, with data type int32, int64, float32, float64, float16, complex64 or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor. Output of Square operator, a Tensor with shape same as input.
Examples
>>> import paddle >>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3]) >>> out = paddle.square(x) >>> print(out) Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [0.16000001, 0.04000000, 0.01000000, 0.09000000])
-
square_
(
name=None
)
square_¶
-
Inplace version of
squareAPI, the output Tensor will be inplaced with inputx. Please refer to square.
-
squeeze
(
axis: int | Sequence[int] | None = None,
name: str | None = None
)
Tensor
squeeze¶
-
Squeeze the dimension(s) of size 1 of input tensor x’s shape.
Note that the output Tensor will share data with origin Tensor and doesn’t have a Tensor copy in
dygraphmode. If you want to use the Tensor copy version, please use Tensor.clone likesqueeze_clone_x = x.squeeze().clone().If axis is provided, it will remove the dimension(s) by given axis that of size 1. If the dimension of given axis is not of size 1, the dimension remain unchanged. If axis is not provided, all dims equal of size 1 will be removed.
Case1: Input: x.shape = [1, 3, 1, 5] # If axis is not provided, all dims equal of size 1 will be removed. axis = None Output: out.shape = [3, 5] Case2: Input: x.shape = [1, 3, 1, 5] # If axis is provided, it will remove the dimension(s) by given axis that of size 1. axis = 0 Output: out.shape = [3, 1, 5] Case4: Input: x.shape = [1, 3, 1, 5] # If the dimension of one given axis (3) is not of size 1, the dimension remain unchanged. axis = [0, 2, 3] Output: out.shape = [3, 5] Case4: Input: x.shape = [1, 3, 1, 5] # If axis is negative, axis = axis + ndim (number of dimensions in x). axis = [-2] Output: out.shape = [1, 3, 5]Note
Alias Support: The parameter name
inputcan be used as an alias forx, anddimcan be used as an alias foraxis. For example,squeeze(input=tensor_x, dim=1)is equivalent tosqueeze(x=tensor_x, axis=1).- Parameters
-
x (Tensor) – The input Tensor. Supported data type: float32, float64, bool, int8, int32, int64. alias:
input.axis (int|list|tuple, optional) –
- An integer or list/tuple of integers, indicating the dimensions to be squeezed. Default is None.
-
The range of axis is \([-ndim(x), ndim(x))\). If axis is negative, \(axis = axis + ndim(x)\). If axis is None, all the dimensions of x of size 1 will be removed.
alias:
dim.name (str|None, optional) – Please refer to api_guide_Name, Default None.
- Returns
-
Tensor, Squeezed Tensor with the same data type as input Tensor.
Examples
>>> import paddle >>> x = paddle.rand([5, 1, 10]) >>> output = paddle.squeeze(x, axis=1) >>> print(x.shape) [5, 1, 10] >>> print(output.shape) [5, 10] >>> # output shares data with x in dygraph mode >>> x[0, 0, 0] = 10. >>> print(output[0, 0]) Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 10.)
-
squeeze_
(
axis: int | Sequence[int] | None = None,
name: str | None = None
)
Tensor
squeeze_¶
-
Inplace version of
squeezeAPI, the output Tensor will be inplaced with inputx. Please refer to api_paddle_tensor_squeeze.
-
stack
(
axis: int = 0,
name: str | None = None,
*,
out: Tensor | None = None
)
Tensor
stack¶
-
Stacks all the input tensors
xalongaxisdimension. All tensors must be of the same shape and same dtype.For example, given N tensors of shape [A, B], if
axis == 0, the shape of stacked tensor is [N, A, B]; ifaxis == 1, the shape of stacked tensor is [A, N, B], etc.It also supports the operation with zero-size tensors which contain 0 in their shape. See the examples below.
Case 1: Input: x[0].shape = [1, 2] x[0].data = [ [1.0 , 2.0 ] ] x[1].shape = [1, 2] x[1].data = [ [3.0 , 4.0 ] ] x[2].shape = [1, 2] x[2].data = [ [5.0 , 6.0 ] ] Attrs: axis = 0 Output: Out.dims = [3, 1, 2] Out.data =[ [ [1.0, 2.0] ], [ [3.0, 4.0] ], [ [5.0, 6.0] ] ] Case 2: Input: x[0].shape = [1, 2] x[0].data = [ [1.0 , 2.0 ] ] x[1].shape = [1, 2] x[1].data = [ [3.0 , 4.0 ] ] x[2].shape = [1, 2] x[2].data = [ [5.0 , 6.0 ] ] Attrs: axis = 1 or axis = -2 # If axis = -2, axis = axis+ndim(x[0])+1 = -2+2+1 = 1. Output: Out.shape = [1, 3, 2] Out.data =[ [ [1.0, 2.0] [3.0, 4.0] [5.0, 6.0] ] ] Case 3: Input: x[0].shape = [0, 1, 2] x[0].data = [] x[1].shape = [0, 1, 2] x[1].data = [] Attrs: axis = 0 Output: Out.shape = [2, 0, 1, 2] Out.data = [] Case 4: Input: x[0].shape = [0, 1, 2] x[0].data = [] x[1].shape = [0, 1, 2] x[1].data = [] Attrs: axis = 1 Output: Out.shape = [0, 2, 1, 2] Out.data = []The image below demonstrates the Case 1: three 2-dimensional tensors with shape [1, 2] are stacked in the dimension of axis=0 to form a 3-dimensional tensor with shape [3, 1, 2] .
- Parameters
-
x (list[Tensor]|tuple[Tensor]) – Input
xcan be alistortupleof tensors, the Tensors inxmust be of the same shape and dtype. Supported data types: float32, float64, int32, int64. Alias:tensors.axis (int, optional) – The axis along which all inputs are stacked.
axisrange is[-(R+1), R+1), whereRis the number of dimensions of the first input tensorx[0]. Ifaxis < 0,axis = axis+R+1. The default value of axis is 0. Alias:dim.name (str, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
out (Tensor, optional) – The output tensor. If set, the output will be written to this tensor.
- Returns
-
Tensor, The stacked tensor with same data type as input.
Examples
>>> import paddle >>> x1 = paddle.to_tensor([[1.0, 2.0]]) >>> x2 = paddle.to_tensor([[3.0, 4.0]]) >>> x3 = paddle.to_tensor([[5.0, 6.0]]) >>> out = paddle.stack([x1, x2, x3], axis=0) >>> print(out.shape) [3, 1, 2] >>> print(out) Tensor(shape=[3, 1, 2], dtype=float32, place=Place(cpu), stop_gradient=True, [[[1., 2.]], [[3., 4.]], [[5., 6.]]]) >>> out = paddle.stack([x1, x2, x3], axis=-2) >>> print(out.shape) [1, 3, 2] >>> print(out) Tensor(shape=[1, 3, 2], dtype=float32, place=Place(cpu), stop_gradient=True, [[[1., 2.], [3., 4.], [5., 6.]]]) >>> # zero-size tensors >>> x1 = paddle.ones([0, 1, 2]) >>> x2 = paddle.ones([0, 1, 2]) >>> out = paddle.stack([x1, x2], axis=0) >>> print(out.shape) [2, 0, 1, 2] >>> print(out) Tensor(shape=[2, 0, 1, 2], dtype=float32, place=Place(cpu), stop_gradient=True, [[], []]) >>> out = paddle.stack([x1, x2], axis=1) >>> print(out.shape) [0, 2, 1, 2] >>> print(out) Tensor(shape=[0, 2, 1, 2], dtype=float32, place=Place(cpu), stop_gradient=True, [])
-
stanh
(
scale_a: float = 0.67,
scale_b: float = 1.7159,
name: str | None = None
)
Tensor
stanh¶
-
stanh activation.
\[out = b * \frac{e^{a * x} - e^{-a * x}}{e^{a * x} + e^{-a * x}}\]- Parameters
-
x (Tensor) – The input Tensor with data type bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64.
scale_a (float, optional) – The scale factor a of the input. Default is 0.67.
scale_b (float, optional) – The scale factor b of the output. Default is 1.7159.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
A Tensor with the same shape and data type as
x(integer types are autocasted into float32).
Examples
>>> import paddle >>> x = paddle.to_tensor([1.0, 2.0, 3.0, 4.0]) >>> out = paddle.stanh(x, scale_a=0.67, scale_b=1.72) >>> print(out) Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [1.00616539, 1.49927628, 1.65933096, 1.70390463])
-
std
(
axis: int | Sequence[int] | None = None,
unbiased: bool = True,
keepdim: bool = False,
name: str | None = None
)
Tensor
std¶
-
Computes the standard-deviation of
xalongaxis.- Parameters
-
x (Tensor) – The input Tensor with data type float16, float32, float64.
axis (int|list|tuple|None, optional) – The axis along which to perform standard-deviation calculations.
axisshould be int, list(int) or tuple(int). Ifaxisis a list/tuple of dimension(s), standard-deviation is calculated along all element(s) ofaxis.axisor element(s) ofaxisshould be in range [-D, D), where D is the dimensions ofx. Ifaxisor element(s) ofaxisis less than 0, it works the same way as \(axis + D\) . Ifaxisis None, standard-deviation is calculated over all elements ofx. Default is None.unbiased (bool, optional) – Whether to use the unbiased estimation. If
unbiasedis True, the standard-deviation is calculated via the unbiased estimator. Ifunbiasedis True, the divisor used in the computation is \(N - 1\), where \(N\) represents the number of elements alongaxis, otherwise the divisor is \(N\). Default is True.keepdim (bool, optional) – Whether to reserve the reduced dimension(s) in the output Tensor. If
keepdimis True, the dimensions of the output Tensor is the same asxexcept in the reduced dimensions(it is of size 1 in this case). Otherwise, the shape of the output Tensor is squeezed inaxis. Default is False.name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, results of standard-deviation along
axisofx, with the same data type asx.
Examples
>>> import paddle >>> x = paddle.to_tensor([[1.0, 2.0, 3.0], [1.0, 4.0, 5.0]]) >>> out1 = paddle.std(x) >>> print(out1.numpy()) 1.6329932 >>> out2 = paddle.std(x, unbiased=False) >>> print(out2.numpy()) 1.490712 >>> out3 = paddle.std(x, axis=1) >>> print(out3.numpy()) [1. 2.081666]
-
stft
(
n_fft: int,
hop_length: int | None = None,
win_length: int | None = None,
window: Tensor | None = None,
center: bool = True,
pad_mode: Literal['reflect', 'constant'] = 'reflect',
normalized: bool = False,
onesided: bool | None = None,
name: str | None = None
)
Tensor
stft¶
-
Short-time Fourier transform (STFT).
The STFT computes the discrete Fourier transforms (DFT) of short overlapping windows of the input using this formula:
\[X_t[f] = \sum_{n = 0}^{N-1} \text{window}[n]\ x[t \times H + n]\ e^{-{2 \pi j f n}/{N}}\]Where: - \(t\): The \(t\)-th input window. - \(f\): Frequency \(0 \leq f < \text{n_fft}\) for onesided=False, or \(0 \leq f < \lfloor \text{n_fft} / 2 \rfloor + 1\) for onesided=True. - \(N\): Value of n_fft. - \(H\): Value of hop_length.
- Parameters
-
x (Tensor) – The input data which is a 1-dimensional or 2-dimensional Tensor with shape […, seq_length]. It can be a real-valued or a complex Tensor.
n_fft (int) – The number of input samples to perform Fourier transform.
hop_length (int|None, optional) – Number of steps to advance between adjacent windows and 0 < hop_length. Default: None (treated as equal to n_fft//4)
win_length (int|None, optional) – The size of window. Default: None (treated as equal to n_fft)
window (Tensor|None, optional) – A 1-dimensional tensor of size win_length. It will be center padded to length n_fft if win_length < n_fft. Default: None ( treated as a rectangle window with value equal to 1 of size win_length).
center (bool, optional) – Whether to pad x to make that the \(t \times hop\_length\) at the center of \(t\)-th frame. Default: True.
pad_mode (str, optional) – Choose padding pattern when center is True. See paddle.nn.functional.pad for all padding options. Default: “reflect”
normalized (bool, optional) – Control whether to scale the output by 1/sqrt(n_fft). Default: False
onesided (bool, optional) – Control whether to return half of the Fourier transform output that satisfies the conjugate symmetry condition when input is a real-valued tensor. It can not be True if input is a complex tensor. Default: None
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
- Returns
-
The complex STFT output tensor with shape […, n_fft//2 + 1, num_frames] (real-valued input and onesided is True) or […, n_fft, num_frames] (onesided is False)
Examples
>>> import paddle >>> from paddle.signal import stft >>> # real-valued input >>> x = paddle.randn([8, 48000], dtype=paddle.float64) >>> y1 = stft(x, n_fft=512) >>> print(y1.shape) [8, 257, 376] >>> y2 = stft(x, n_fft=512, onesided=False) >>> print(y2.shape) [8, 512, 376] >>> # complex input >>> x = paddle.randn([8, 48000], dtype=paddle.float64) + \ ... paddle.randn([8, 48000], dtype=paddle.float64)*1j >>> print(x.shape) [8, 48000] >>> print(x.dtype) paddle.complex128 >>> y1 = stft(x, n_fft=512, center=False, onesided=False) >>> print(y1.shape) [8, 512, 372]
-
strided_slice
(
axes: Sequence[int | Tensor],
starts: Sequence[int | Tensor] | Tensor,
ends: Sequence[int | Tensor] | Tensor,
strides: Sequence[int | Tensor] | Tensor,
name: str | None = None
)
Tensor
strided_slice¶
-
This operator produces a slice of
xalong multiple axes. Similar to numpy: https://docs.scipy.org/doc/numpy/reference/arrays.indexing.html Slice usesaxes,startsandendsattributes to specify the start and end dimension for each axis in the list of axes and Slice uses this information to slice the input data tensor. If a negative value is passed tostartsorendssuch as \(-i\), it represents the reverse position of the axis \(i-1\) th(here 0 is the initial position). Thestridesrepresents steps of slicing and if thestridesis negative, slice operation is in the opposite direction. If the value passed tostartsorendsis greater than n (the number of elements in this dimension), it represents n. For slicing to the end of a dimension with unknown size, it is recommended to pass in INT_MAX. The size ofaxesmust be equal tostarts,endsandstrides. Following examples will explain how strided_slice works:Case1: Given: data = [ [1, 2, 3, 4], [5, 6, 7, 8], ] axes = [0, 1] starts = [1, 0] ends = [2, 3] strides = [1, 1] Then: result = [ [5, 6, 7], ] Case2: Given: data = [ [1, 2, 3, 4], [5, 6, 7, 8], ] axes = [0, 1] starts = [0, 1] ends = [2, 0] strides = [1, -1] Then: result = [ [8, 7, 6], ] Case3: Given: data = [ [1, 2, 3, 4], [5, 6, 7, 8], ] axes = [0, 1] starts = [0, 1] ends = [-1, 1000] strides = [1, 3] Then: result = [ [2], ]- Parameters
-
x (Tensor) – An N-D
Tensor. The data type isbool,float16,float32,float64,int32orint64.axes (list|tuple) – The data type is
int32. Axes that starts and ends apply to. It’s optional. If it is not provides, it will be treated as \([0,1,...,len(starts)-1]\).starts (list|tuple|Tensor) – The data type is
int32. Ifstartsis a list or tuple, the elements of it should be integers or Tensors with shape []. Ifstartsis an Tensor, it should be an 1-D Tensor. It represents starting indices of corresponding axis inaxes.ends (list|tuple|Tensor) – The data type is
int32. Ifendsis a list or tuple, the elements of it should be integers or Tensors with shape []. Ifendsis an Tensor, it should be an 1-D Tensor. It represents ending indices of corresponding axis inaxes.strides (list|tuple|Tensor) – The data type is
int32. Ifstridesis a list or tuple, the elements of it should be integers or Tensors with shape []. Ifstridesis an Tensor, it should be an 1-D Tensor. It represents slice step of corresponding axis inaxes.name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name .
- Returns
-
Tensor, A
Tensorwith the same dimension asx. The data type is same asx.
Examples
>>> import paddle >>> x = paddle.zeros(shape=[3,4,5,6], dtype="float32") >>> # example 1: >>> # attr starts is a list which doesn't contain Tensor. >>> axes = [1, 2, 3] >>> starts = [-3, 0, 2] >>> ends = [3, 2, 4] >>> strides_1 = [1, 1, 1] >>> strides_2 = [1, 1, 2] >>> sliced_1 = paddle.strided_slice(x, axes=axes, starts=starts, ends=ends, strides=strides_1) >>> # sliced_1 is x[:, 1:3:1, 0:2:1, 2:4:1]. >>> # example 2: >>> # attr starts is a list which contain tensor Tensor. >>> minus_3 = paddle.full(shape=[1], fill_value=-3, dtype='int32') >>> sliced_2 = paddle.strided_slice(x, axes=axes, starts=[minus_3, 0, 2], ends=ends, strides=strides_2) >>> # sliced_2 is x[:, 1:3:1, 0:2:1, 2:4:2].
-
subtract
(
y: Tensor,
name: str | None = None
)
Tensor
subtract¶
-
Subtract two tensors element-wise. The equation is:
\[out = x - y\]Note
paddle.subtractsupports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .- Parameters
-
x (Tensor) – the input tensor, it’s data type should be bfloat16, float16, float32, float64, int16, int32, int64, complex64, complex128.
y (Tensor) – the input tensor, it’s data type should be bfloat16, float16, float32, float64, int16, int32, int64, complex64, complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
N-D Tensor. A location into which the result is stored. If x, y have different shapes and are “broadcastable”, the resulting tensor shape is the shape of x and y after broadcasting. If x, y have the same shape, its shape is the same as x and y.
Examples
>>> import paddle >>> x = paddle.to_tensor([[1, 2], [7, 8]]) >>> y = paddle.to_tensor([[5, 6], [3, 4]]) >>> res = paddle.subtract(x, y) >>> print(res) Tensor(shape=[2, 2], dtype=int64, place=Place(cpu), stop_gradient=True, [[-4, -4], [ 4, 4]]) >>> x = paddle.to_tensor([[[1, 2, 3], [1, 2, 3]]]) >>> y = paddle.to_tensor([1, 0, 4]) >>> res = paddle.subtract(x, y) >>> print(res) Tensor(shape=[1, 2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[[ 0, 2, -1], [ 0, 2, -1]]]) >>> x = paddle.to_tensor([2, float('nan'), 5], dtype='float32') >>> y = paddle.to_tensor([1, 4, float('nan')], dtype='float32') >>> res = paddle.subtract(x, y) >>> print(res) Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True, [1. , nan, nan]) >>> x = paddle.to_tensor([5, float('inf'), -float('inf')], dtype='float64') >>> y = paddle.to_tensor([1, 4, 5], dtype='float64') >>> res = paddle.subtract(x, y) >>> print(res) Tensor(shape=[3], dtype=float64, place=Place(cpu), stop_gradient=True, [ 4. , inf., -inf.])
-
subtract_
(
y: Tensor,
name: str | None = None
)
Tensor
subtract_¶
-
Inplace version of
subtractAPI, the output Tensor will be inplaced with inputx. Please refer to subtract.
-
sum
(
axis: int | Sequence[int] | None = None,
dtype: DTypeLike | None = None,
keepdim: bool = False,
name: str | None = None
)
Tensor
sum¶
-
Computes the sum of tensor elements over the given dimension.
Note
Parameter order support: When passing positional parameters, it is possible to support swapping the positional order of dtype and axis. For example,
sum(x, axis, keepdim, dtype)is equivalent tosum(x, axis, dtype, keepdim). Alias Support: The parameter nameinputcan be used as an alias forxand the parameter namedimcan be used as an alias foraxis. For example,sum(input=tensor_x, dim=1)is equivalent tosum(x=tensor_x, axis=1).- Parameters
-
x (Tensor) – An N-D Tensor, the data type is bool, bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64, complex64, complex128. alias:
input.axis (int|list|tuple|None, optional) – The dimensions along which the sum is performed. If
None, sum all elements ofxand return a Tensor with a single element, otherwise must be in the range \([-rank(x), rank(x))\). If \(axis[i] < 0\), the dimension to reduce is \(rank + axis[i]\). alias:dim.dtype (str|paddle.dtype|np.dtype, optional) – The dtype of output Tensor. The default value is None, the dtype of output is the same as input Tensor x.
keepdim (bool, optional) – Whether to reserve the reduced dimension in the output Tensor. The result Tensor will have one fewer dimension than the
xunlesskeepdimis true, default value is False.name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Results of summation operation on the specified axis of input Tensor x, if x.dtype=’bool’, x.dtype=’int32’, it’s data type is ‘int64’, otherwise it’s data type is the same as x.
- Return type
-
Tensor
Examples
>>> import paddle >>> # x is a Tensor with following elements: >>> # [[0.2, 0.3, 0.5, 0.9] >>> # [0.1, 0.2, 0.6, 0.7]] >>> # Each example is followed by the corresponding output tensor. >>> x = paddle.to_tensor([[0.2, 0.3, 0.5, 0.9], ... [0.1, 0.2, 0.6, 0.7]]) >>> out1 = paddle.sum(x) >>> out1 Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 3.50000000) >>> out2 = paddle.sum(x, axis=0) >>> out2 Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [0.30000001, 0.50000000, 1.10000002, 1.59999990]) >>> out3 = paddle.sum(x, axis=-1) >>> out3 Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True, [1.89999998, 1.60000002]) >>> out4 = paddle.sum(x, axis=1, keepdim=True) >>> out4 Tensor(shape=[2, 1], dtype=float32, place=Place(cpu), stop_gradient=True, [[1.89999998], [1.60000002]]) >>> # y is a Tensor with shape [2, 2, 2] and elements as below: >>> # [[[1, 2], [3, 4]], >>> # [[5, 6], [7, 8]]] >>> # Each example is followed by the corresponding output tensor. >>> y = paddle.to_tensor([[[1, 2], [3, 4]], ... [[5, 6], [7, 8]]]) >>> out5 = paddle.sum(y, axis=[1, 2]) >>> out5 Tensor(shape=[2], dtype=int64, place=Place(cpu), stop_gradient=True, [10, 26]) >>> out6 = paddle.sum(y, axis=[0, 1]) >>> out6 Tensor(shape=[2], dtype=int64, place=Place(cpu), stop_gradient=True, [16, 20]) >>> # x is a Tensor with following elements: >>> # [[True, True, True, True] >>> # [False, False, False, False]] >>> # Each example is followed by the corresponding output tensor. >>> x = paddle.to_tensor([[True, True, True, True], ... [False, False, False, False]]) >>> out7 = paddle.sum(x) >>> out7 Tensor(shape=[], dtype=int64, place=Place(cpu), stop_gradient=True, 4) >>> out8 = paddle.sum(x, axis=0) >>> out8 Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True, [1, 1, 1, 1]) >>> out9 = paddle.sum(x, axis=1) >>> out9 Tensor(shape=[2], dtype=int64, place=Place(cpu), stop_gradient=True, [4, 0])
-
svd_lowrank
(
q: int | None = None,
niter: int = 2,
M: Tensor | None = None,
name: str | None = None
)
tuple[Tensor, Tensor, Tensor]
svd_lowrank¶
-
Return the singular value decomposition (SVD) on a low-rank matrix or batches of such matrices.
If \(X\) is the input matrix or a batch of input matrices, the output should satisfies:
\[X \approx U * diag(S) * V^{H}\]When \(M\) is given, the output should satisfies:
\[X - M \approx U * diag(S) * V^{H}\]- Parameters
-
x (Tensor) – The input tensor. Its shape should be […, N, M], where … is zero or more batch dimensions. N and M can be arbitrary positive number. The data type of
xshould be float32 or float64.q (int, optional) – A slightly overestimated rank of \(X\). Default value is None, which means the overestimated rank is 6.
niter (int, optional) – The number of iterations to perform. Default: 2.
M (Tensor, optional) – The input tensor’s mean. Its shape should be […, 1, M]. Default value is None.
name (str|None, optional) – Name for the operation. For more information, please refer to api_guide_Name. Default: None.
- Returns
-
Tensor U, is N x q matrix.
Tensor S, is a vector with length q.
Tensor V, is M x q matrix.
tuple (U, S, V): which is the nearly optimal approximation of a singular value decomposition of the matrix \(X\) or \(X - M\).
Examples
>>> import paddle >>> paddle.seed(2024) >>> x = paddle.randn((5, 5), dtype='float64') >>> U, S, V = paddle.linalg.svd_lowrank(x) >>> print(U) Tensor(shape=[5, 5], dtype=float64, place=Place(cpu), stop_gradient=True, [[-0.03586982, -0.17211503, 0.31536566, -0.38225676, -0.85059629], [-0.38386839, 0.67754925, 0.23222694, 0.51777188, -0.26749766], [-0.85977150, -0.28442378, -0.41412094, -0.08955629, -0.01948348], [ 0.18611503, 0.56047358, -0.67717019, -0.39286761, -0.19577062], [ 0.27841082, -0.34099254, -0.46535957, 0.65071250, -0.40770727]]) >>> print(S) Tensor(shape=[5], dtype=float64, place=Place(cpu), stop_gradient=True, [4.11253399, 3.03227120, 2.45499752, 1.25602436, 0.45825337]) >>> print(V) Tensor(shape=[5, 5], dtype=float64, place=Place(cpu), stop_gradient=True, [[ 0.46401347, 0.50977695, -0.08742316, -0.11140428, -0.71046833], [-0.48927226, -0.35047624, 0.07918771, 0.45431083, -0.65200463], [-0.20494730, 0.67097011, -0.05427719, 0.66510472, 0.24997083], [-0.69645001, 0.40237917, 0.09360970, -0.58032322, -0.08666357], [ 0.13512270, 0.07199989, 0.98710572, 0.04529277, 0.01134594]])
-
swapaxes
(
perm: Sequence[int],
name: str | None = None
)
Tensor
swapaxes¶
-
Permute the data dimensions of input according to perm.
The i-th dimension of the returned tensor will correspond to the perm[i]-th dimension of input.
Note
Alias Support: The parameter name
inputcan be used as an alias forx, anddim0&dim1can replaceperm. For example,transpose(input=x, dim0=0, dim1=1)is equivalent totranspose(x=x, perm=[1, 0, 2]).- Parameters
-
x (Tensor) – The input Tensor. It is a N-D Tensor of data types bool, float16, bfloat16, float32, float64, int8, int16, int32, int64, uint8, uint16, complex64, complex128. alias:
input.perm (list|tuple) – Permute the input according to the data of perm.
name (str|None, optional) – The name of this layer. For more information, please refer to api_guide_Name. Default is None.
- Returns
-
A transposed n-D Tensor, with data type being bool, float32, float64, int32, int64.
- Return type
-
Tensor
Examples
# The following codes in this code block are pseudocode, designed to show the execution logic and results of the function. x = to_tensor([[[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]] [[13 14 15 16] [17 18 19 20] [21 22 23 24]]]) shape(x): return [2,3,4] # Example 1 perm0 = [1,0,2] y_perm0 = transpose(x, perm0) # Permute x by perm0 # dim:0 of y_perm0 is dim:1 of x # dim:1 of y_perm0 is dim:0 of x # dim:2 of y_perm0 is dim:2 of x # The above two lines can also be understood as exchanging the zeroth and first dimensions of x y_perm0.data = [[[ 1 2 3 4] [13 14 15 16]] [[ 5 6 7 8] [17 18 19 20]] [[ 9 10 11 12] [21 22 23 24]]] shape(y_perm0): return [3,2,4] # Example 2 perm1 = [2,1,0] y_perm1 = transpose(x, perm1) # Permute x by perm1 # dim:0 of y_perm1 is dim:2 of x # dim:1 of y_perm1 is dim:1 of x # dim:2 of y_perm1 is dim:0 of x # The above two lines can also be understood as exchanging the zeroth and second dimensions of x y_perm1.data = [[[ 1 13] [ 5 17] [ 9 21]] [[ 2 14] [ 6 18] [10 22]] [[ 3 15] [ 7 19] [11 23]] [[ 4 16] [ 8 20] [12 24]]] shape(y_perm1): return [4,3,2]Examples
>>> import paddle >>> x = paddle.randn([2, 3, 4]) >>> x_transposed = paddle.transpose(x, perm=[1, 0, 2]) >>> print(x_transposed.shape) [3, 2, 4]
-
swapdims
(
perm: Sequence[int],
name: str | None = None
)
Tensor
swapdims¶
-
Permute the data dimensions of input according to perm.
The i-th dimension of the returned tensor will correspond to the perm[i]-th dimension of input.
Note
Alias Support: The parameter name
inputcan be used as an alias forx, anddim0&dim1can replaceperm. For example,transpose(input=x, dim0=0, dim1=1)is equivalent totranspose(x=x, perm=[1, 0, 2]).- Parameters
-
x (Tensor) – The input Tensor. It is a N-D Tensor of data types bool, float16, bfloat16, float32, float64, int8, int16, int32, int64, uint8, uint16, complex64, complex128. alias:
input.perm (list|tuple) – Permute the input according to the data of perm.
name (str|None, optional) – The name of this layer. For more information, please refer to api_guide_Name. Default is None.
- Returns
-
A transposed n-D Tensor, with data type being bool, float32, float64, int32, int64.
- Return type
-
Tensor
Examples
# The following codes in this code block are pseudocode, designed to show the execution logic and results of the function. x = to_tensor([[[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]] [[13 14 15 16] [17 18 19 20] [21 22 23 24]]]) shape(x): return [2,3,4] # Example 1 perm0 = [1,0,2] y_perm0 = transpose(x, perm0) # Permute x by perm0 # dim:0 of y_perm0 is dim:1 of x # dim:1 of y_perm0 is dim:0 of x # dim:2 of y_perm0 is dim:2 of x # The above two lines can also be understood as exchanging the zeroth and first dimensions of x y_perm0.data = [[[ 1 2 3 4] [13 14 15 16]] [[ 5 6 7 8] [17 18 19 20]] [[ 9 10 11 12] [21 22 23 24]]] shape(y_perm0): return [3,2,4] # Example 2 perm1 = [2,1,0] y_perm1 = transpose(x, perm1) # Permute x by perm1 # dim:0 of y_perm1 is dim:2 of x # dim:1 of y_perm1 is dim:1 of x # dim:2 of y_perm1 is dim:0 of x # The above two lines can also be understood as exchanging the zeroth and second dimensions of x y_perm1.data = [[[ 1 13] [ 5 17] [ 9 21]] [[ 2 14] [ 6 18] [10 22]] [[ 3 15] [ 7 19] [11 23]] [[ 4 16] [ 8 20] [12 24]]] shape(y_perm1): return [4,3,2]Examples
>>> import paddle >>> x = paddle.randn([2, 3, 4]) >>> x_transposed = paddle.transpose(x, perm=[1, 0, 2]) >>> print(x_transposed.shape) [3, 2, 4]
-
t
(
name: str | None = None
)
Tensor
t¶
-
Transpose <=2-D tensor. 0-D and 1-D tensors are returned as it is and 2-D tensor is equal to the paddle.transpose function which perm dimensions set 0 and 1.
- Parameters
-
input (Tensor) – The input Tensor. It is a N-D (N<=2) Tensor of data types float32, float64, int32, int64.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name .
- Returns
-
A transposed n-D Tensor, with data type being float16, float32, float64, int32, int64.
- Return type
-
Tensor
Examples
>>> import paddle >>> # Example 1 (0-D tensor) >>> x = paddle.to_tensor([0.79]) >>> out = paddle.t(x) >>> print(out) Tensor(shape=[1], dtype=float32, place=Place(cpu), stop_gradient=True, [0.79000002]) >>> # Example 2 (1-D tensor) >>> x = paddle.to_tensor([0.79, 0.84, 0.32]) >>> out2 = paddle.t(x) >>> print(out2) Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True, [0.79000002, 0.83999997, 0.31999999]) >>> print(paddle.t(x).shape) [3] >>> # Example 3 (2-D tensor) >>> x = paddle.to_tensor([[0.79, 0.84, 0.32], ... [0.64, 0.14, 0.57]]) >>> print(x.shape) [2, 3] >>> out3 = paddle.t(x) >>> print(out3) Tensor(shape=[3, 2], dtype=float32, place=Place(cpu), stop_gradient=True, [[0.79000002, 0.63999999], [0.83999997, 0.14000000], [0.31999999, 0.56999999]]) >>> print(paddle.t(x).shape) [3, 2]
-
t_
(
name=None
)
t_¶
-
Inplace version of
tAPI, the output Tensor will be inplaced with inputinput. Please refer to t.
-
take
(
index: Tensor,
mode: Literal['raise', 'wrap', 'clip'] = 'raise',
name: str | None = None
)
Tensor
take¶
-
Returns a new tensor with the elements of input tensor x at the given index. The input tensor is treated as if it were viewed as a 1-D tensor. The result takes the same shape as the index.
- Parameters
-
x (Tensor) – An N-D Tensor, its data type should be int32, int64, float32, float64.
index (Tensor) – An N-D Tensor, its data type should be int32, int64.
mode (str, optional) –
Specifies how out-of-bounds index will behave. the candidates are
'raise','wrap'and'clip'.'raise': raise an error (default);'wrap': wrap around;'clip': clip to the range.'clip'mode means that all indices that are too large are replaced by the index that addresses the last element. Note that this disables indexing with negative numbers.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, Tensor with the same shape as index, the data type is the same with input.
Examples
>>> import paddle >>> x_int = paddle.arange(0, 12).reshape([3, 4]) >>> x_float = x_int.astype(paddle.float64) >>> idx_pos = paddle.arange(4, 10).reshape([2, 3]) # positive index >>> idx_neg = paddle.arange(-2, 4).reshape([2, 3]) # negative index >>> idx_err = paddle.arange(-2, 13).reshape([3, 5]) # index out of range >>> paddle.take(x_int, idx_pos) Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[4, 5, 6], [7, 8, 9]]) >>> paddle.take(x_int, idx_neg) Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[10, 11, 0 ], [1 , 2 , 3 ]]) >>> paddle.take(x_float, idx_pos) Tensor(shape=[2, 3], dtype=float64, place=Place(cpu), stop_gradient=True, [[4., 5., 6.], [7., 8., 9.]]) >>> x_int.take(idx_pos) Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[4, 5, 6], [7, 8, 9]]) >>> paddle.take(x_int, idx_err, mode='wrap') Tensor(shape=[3, 5], dtype=int64, place=Place(cpu), stop_gradient=True, [[10, 11, 0 , 1 , 2 ], [3 , 4 , 5 , 6 , 7 ], [8 , 9 , 10, 11, 0 ]]) >>> paddle.take(x_int, idx_err, mode='clip') Tensor(shape=[3, 5], dtype=int64, place=Place(cpu), stop_gradient=True, [[0 , 0 , 0 , 1 , 2 ], [3 , 4 , 5 , 6 , 7 ], [8 , 9 , 10, 11, 11]])
-
take_along_axis
(
indices: Tensor,
axis: int,
broadcast: bool = True,
*,
out: Tensor | None = None
)
Tensor
take_along_axis¶
-
Take values from the input array by given indices matrix along the designated axis.
Note
Alias Support: The parameter name
inputcan be used as an alias forarr, anddimcan be used as an alias foraxis. For example,repeat_interleave(input=tensor_arr, dim=1, ...)is equivalent torepeat_interleave(arr=tensor_arr, axis=1, ...).- Parameters
-
arr (Tensor) – The input Tensor. Supported data types are bfloat16, float16, float32, float64, int32, int64, uint8. alias:
input.indices (Tensor) – Indices to take along each 1d slice of arr. This must match the dimension of arr, and need to broadcast against arr. Supported data type are int32 and int64.
axis (int) – The axis to take 1d slices along. alias:
dim.broadcast (bool, optional) – whether the indices broadcast.
out (Tensor, optional) – The output Tensor. If set, the output will be written to this Tensor.
- Returns
-
Tensor, The indexed element, same dtype with arr.
Examples
>>> import paddle >>> x = paddle.to_tensor([[1, 2, 3], [4, 5, 6], [7,8,9]]) >>> index = paddle.to_tensor([[0]]) >>> axis = 0 >>> result = paddle.take_along_axis(x, index, axis) >>> print(result) Tensor(shape=[1, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[1, 2, 3]])
-
take_along_dim
(
indices: Tensor,
axis: int,
broadcast: bool = True,
*,
out: Tensor | None = None
)
Tensor
take_along_dim¶
-
Take values from the input array by given indices matrix along the designated axis.
Note
Alias Support: The parameter name
inputcan be used as an alias forarr, anddimcan be used as an alias foraxis. For example,repeat_interleave(input=tensor_arr, dim=1, ...)is equivalent torepeat_interleave(arr=tensor_arr, axis=1, ...).- Parameters
-
arr (Tensor) – The input Tensor. Supported data types are bfloat16, float16, float32, float64, int32, int64, uint8. alias:
input.indices (Tensor) – Indices to take along each 1d slice of arr. This must match the dimension of arr, and need to broadcast against arr. Supported data type are int32 and int64.
axis (int) – The axis to take 1d slices along. alias:
dim.broadcast (bool, optional) – whether the indices broadcast.
out (Tensor, optional) – The output Tensor. If set, the output will be written to this Tensor.
- Returns
-
Tensor, The indexed element, same dtype with arr.
Examples
>>> import paddle >>> x = paddle.to_tensor([[1, 2, 3], [4, 5, 6], [7,8,9]]) >>> index = paddle.to_tensor([[0]]) >>> axis = 0 >>> result = paddle.take_along_axis(x, index, axis) >>> print(result) Tensor(shape=[1, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[1, 2, 3]])
-
tan
(
name: str | None = None
)
Tensor
tan¶
-
Tangent Operator. Computes tangent of x element-wise.
Input range is (k*pi-pi/2, k*pi+pi/2) and output range is (-inf, inf).
\[out = tan(x)\]- Parameters
-
x (Tensor) – Input of Tan operator, an N-D Tensor, with data type float32, float64, float16, bfloat16, uint8, int8, int16, int32, int64, complex64 or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
- Tensor. Output of Tan operator, a Tensor with shape same as input
-
(integer types are autocasted into float32).
Examples
>>> import paddle >>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3]) >>> out = paddle.tan(x) >>> print(out) Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [-0.42279324, -0.20271003, 0.10033467, 0.30933627])
-
tan_
(
name=None
)
tan_¶
-
Inplace version of
tanAPI, the output Tensor will be inplaced with inputx. Please refer to tan.
-
tanh
(
name: str | None = None
)
Tensor
tanh¶
-
Tanh Activation Operator.
\[out = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}\]- Parameters
-
x (Tensor) – Input of Tanh operator, an N-D Tensor, with data type bfloat16, float32, float64, float16, uint8, int8, int16, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
- Output of Tanh operator, a Tensor with same data type and shape as input
-
(integer types are autocasted into float32).
Examples
>>> import paddle >>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3]) >>> out = paddle.tanh(x) >>> out Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [-0.37994900, -0.19737528, 0.09966799, 0.29131261])
-
tanh_
(
name: str | None = None
)
Tensor
tanh_¶
-
Inplace version of
tanhAPI, the output Tensor will be inplaced with inputx. Please refer to tanh.
-
tensor_split
(
num_or_indices: int | Sequence[int],
axis: int | Tensor = 0,
name: str | None = None
)
list[Tensor]
tensor_split¶
-
Split the input tensor into multiple sub-Tensors along
axis, allowing not being of equal size.In the following figure, the shape of Tenser x is [6], and after paddle.tensor_split(x, num_or_indices=4) transformation, we get four sub-Tensors out0, out1, out2, and out3 :
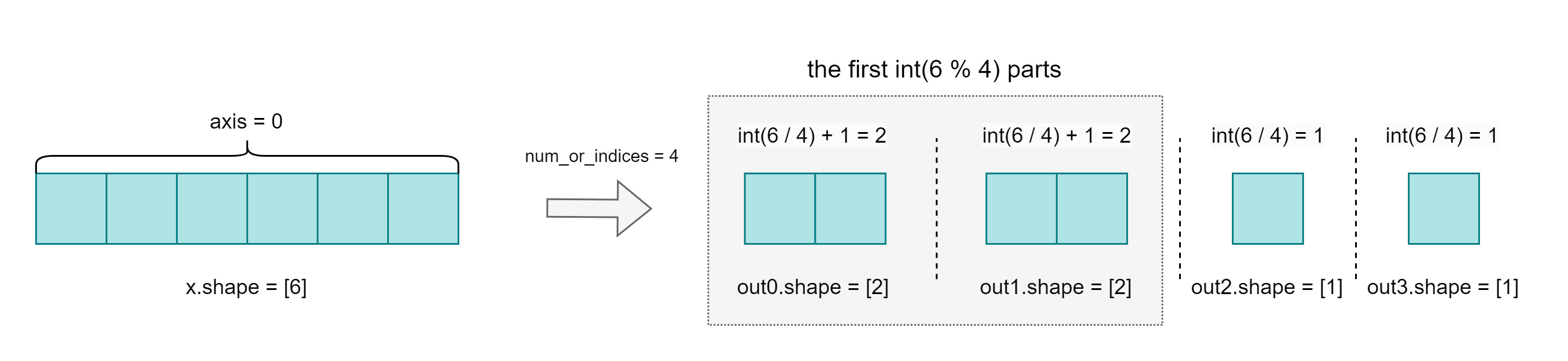
since the length of x in axis = 0 direction 6 is not divisible by num_or_indices = 4, the size of the first int(6 % 4) part after splitting will be int(6 / 4) + 1 and the size of the remaining parts will be int(6 / 4).
- Parameters
-
x (Tensor) – A Tensor whose dimension must be greater than 0. The data type is bool, bfloat16, float16, float32, float64, uint8, int32 or int64.
num_or_indices (int|list|tuple) – If
num_or_indicesis an intn,xis split intonsections alongaxis. Ifxis divisible byn, each section will bex.shape[axis] / n. Ifxis not divisible byn, the firstint(x.shape[axis] % n)sections will have sizeint(x.shape[axis] / n) + 1, and the rest will beint(x.shape[axis] / n). If ``num_or_indicesis a list or tuple of integer indices,xis split alongaxisat each of the indices. For instance,num_or_indices=[2, 4]withaxis=0would splitxintox[:2],x[2:4]andx[4:]along axis 0.axis (int|Tensor, optional) – The axis along which to split, it can be a integer or a
0-D Tensorwith shape [] and data typeint32orint64. If :math::axis < 0, the axis to split along is \(rank(x) + axis\). Default is 0.name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name .
- Returns
-
list[Tensor], The list of segmented Tensors.
Examples
>>> import paddle >>> # evenly split >>> # x is a Tensor of shape [8] >>> x = paddle.rand([8]) >>> out0, out1 = paddle.tensor_split(x, num_or_indices=2) >>> print(out0.shape) [4] >>> print(out1.shape) [4]

>>> import paddle >>> # not evenly split >>> # x is a Tensor of shape [8] >>> x = paddle.rand([8]) >>> out0, out1, out2 = paddle.tensor_split(x, num_or_indices=3) >>> print(out0.shape) [3] >>> print(out1.shape) [3] >>> print(out2.shape) [2]
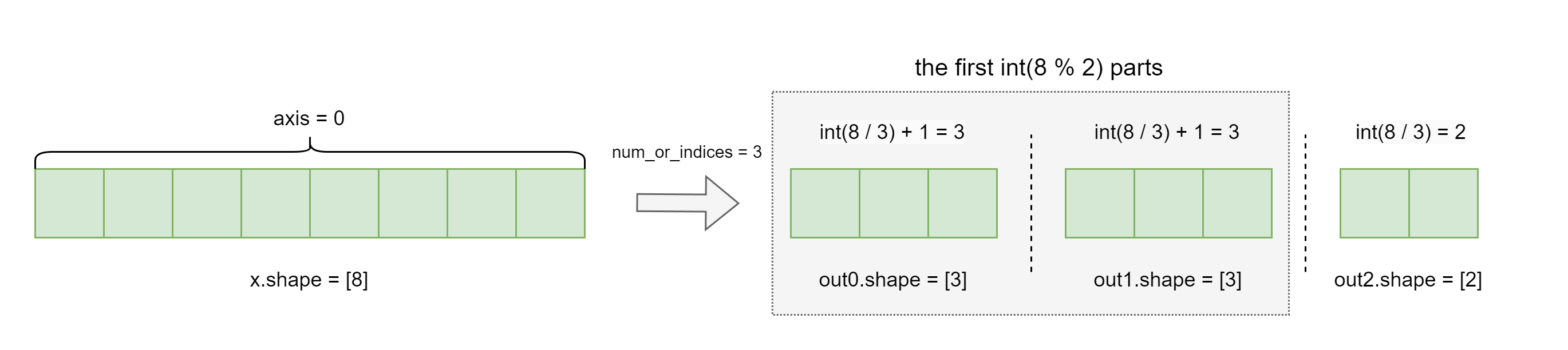
>>> import paddle >>> # split with indices >>> # x is a Tensor of shape [8] >>> x = paddle.rand([8]) >>> out0, out1, out2 = paddle.tensor_split(x, num_or_indices=[2, 3]) >>> print(out0.shape) [2] >>> print(out1.shape) [1] >>> print(out2.shape) [5]

>>> import paddle >>> # split along axis >>> # x is a Tensor of shape [7, 8] >>> x = paddle.rand([7, 8]) >>> out0, out1 = paddle.tensor_split(x, num_or_indices=2, axis=1) >>> print(out0.shape) [7, 4] >>> print(out1.shape) [7, 4]
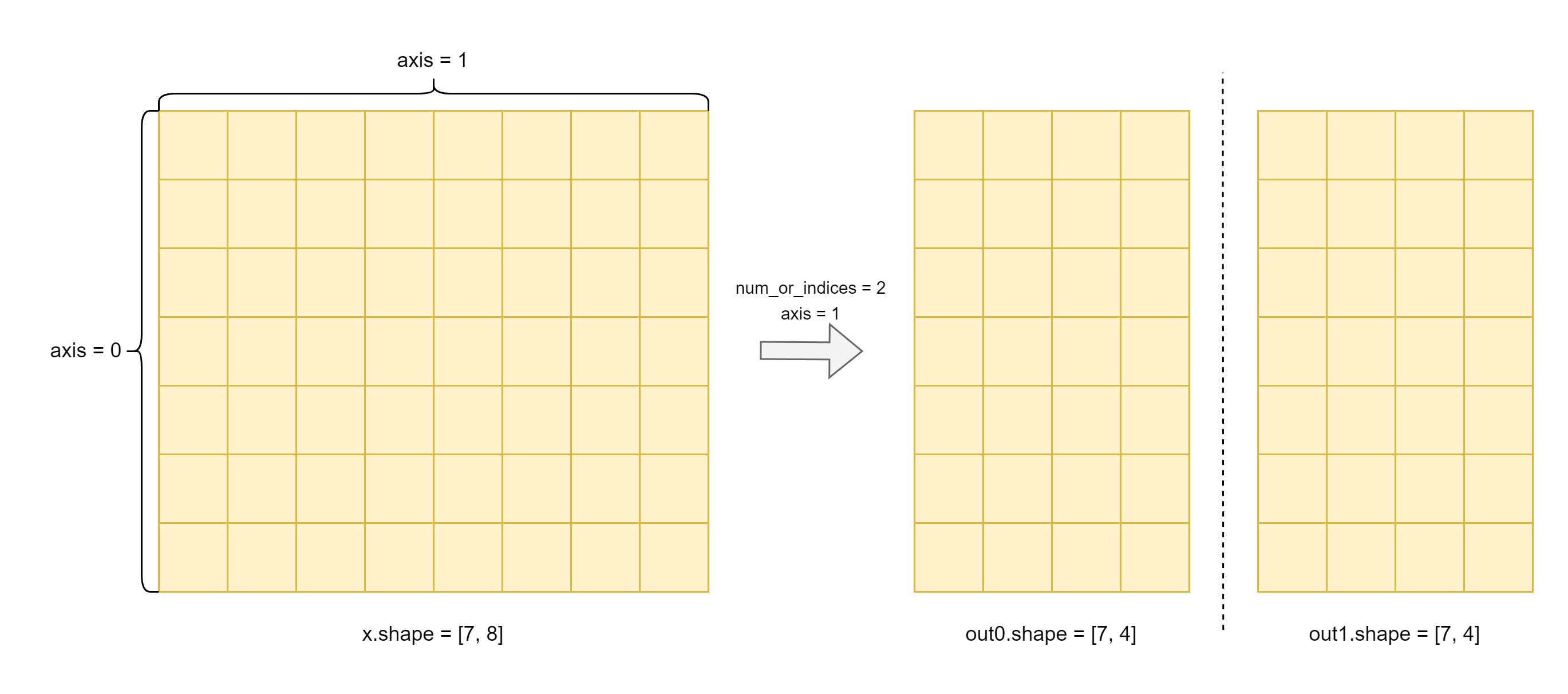
>>> import paddle >>> # split along axis with indices >>> # x is a Tensor of shape [7, 8] >>> x = paddle.rand([7, 8]) >>> out0, out1, out2 = paddle.tensor_split(x, num_or_indices=[2, 3], axis=1) >>> print(out0.shape) [7, 2] >>> print(out1.shape) [7, 1] >>> print(out2.shape) [7, 5]
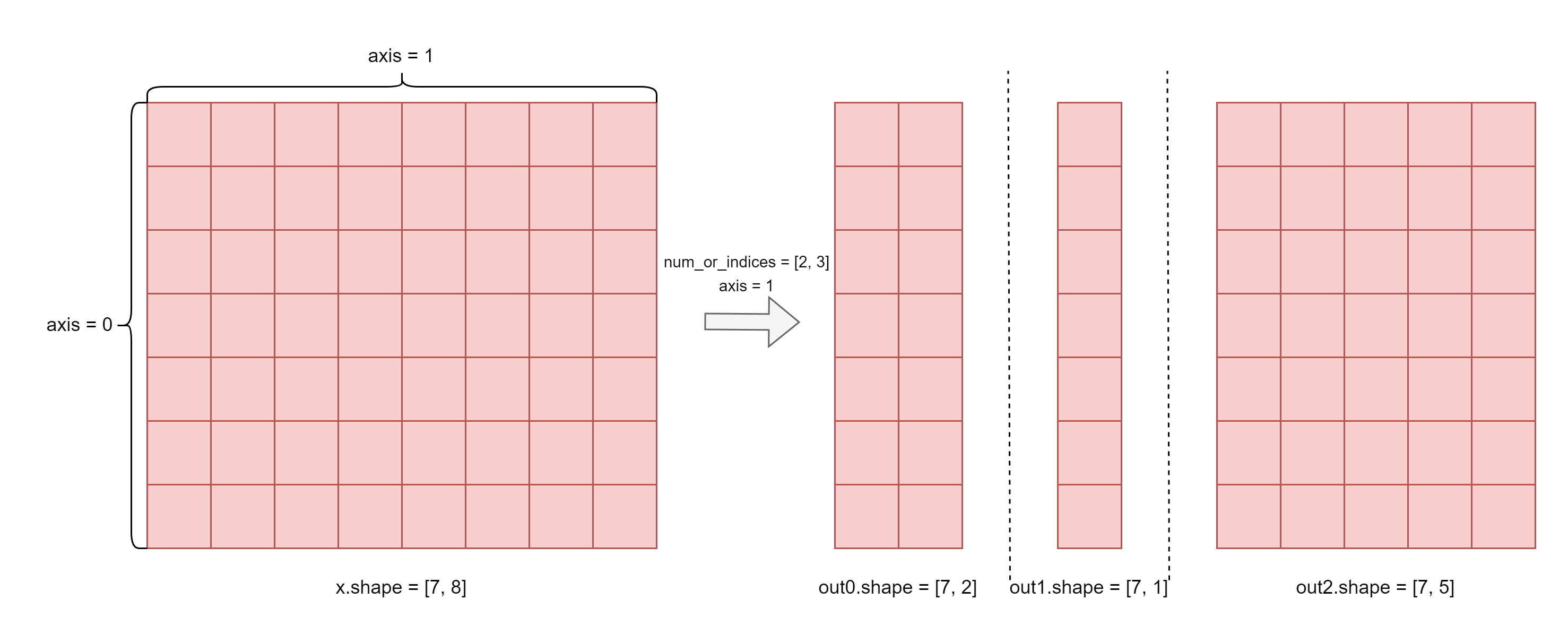
-
tensordot
(
y: Tensor,
axes: int | NestedSequence[int] | Tensor = 2,
name: str | None = None
)
Tensor
tensordot¶
-
This function computes a contraction, which sum the product of elements from two tensors along the given axes.
- Parameters
-
x (Tensor) – The left tensor for contraction with data type
float16orfloat32orfloat64.y (Tensor) – The right tensor for contraction with the same data type as
x.axes (int|tuple|list|Tensor, optional) –
The axes to contract for
xandy, defaulted to integer2.It could be a non-negative integer
n, in which the function will sum over the lastnaxes ofxand the firstnaxes ofyin order.It could be a 1-d tuple or list with data type
int, in whichxandywill be contracted along the same given axes. For example,axes=[0, 1] applies contraction along the first two axes forxand the first two axes fory.It could be a tuple or list containing one or two 1-d tuple|list|Tensor with data type
int. When containing one tuple|list|Tensor, the data in tuple|list|Tensor specified the same axes forxandyto contract. When containing two tuple|list|Tensor, the first will be applied toxand the second toy. When containing more than two tuple|list|Tensor, only the first two axis sequences will be used while the others will be ignored.It could be a tensor, in which the
axestensor will be translated to a python list and applied the same rules described above to determine the contraction axes. Note that theaxeswith Tensor type is ONLY available in Dygraph mode.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name .
- Returns
-
Output (Tensor), The contraction result with the same data type as
xandy. In general, \(output.ndim = x.ndim + y.ndim - 2 \times n_{axes}\), where \(n_{axes}\) denotes the number of axes to be contracted.
Notes
This function supports tensor broadcast, the size in the corresponding dimensions of
xandyshould be equal, or applies to the broadcast rules.This function also supports axes expansion, when the two given axis sequences for
xandyare of different lengths, the shorter sequence will expand the same axes as the longer one at the end. For example, ifaxes=[[0, 1, 2, 3], [1, 0]], the axis sequence forxis [0, 1, 2, 3], while the corresponding axis sequences forywill be expanded from [1, 0] to [1, 0, 2, 3].
Examples
>>> import paddle >>> from typing import Literal >>> data_type: Literal["float64"] = 'float64' >>> # For two 2-d tensor x and y, the case axes=0 is equivalent to outer product. >>> # Note that tensordot supports empty axis sequence, so all the axes=0, axes=[], axes=[[]], and axes=[[],[]] are equivalent cases. >>> x = paddle.arange(4, dtype=data_type).reshape([2, 2]) >>> y = paddle.arange(4, dtype=data_type).reshape([2, 2]) >>> z = paddle.tensordot(x, y, axes=0) >>> print(z) Tensor(shape=[2, 2, 2, 2], dtype=float64, place=Place(cpu), stop_gradient=True, [[[[0., 0.], [0., 0.]], [[0., 1.], [2., 3.]]], [[[0., 2.], [4., 6.]], [[0., 3.], [6., 9.]]]]) >>> # For two 1-d tensor x and y, the case axes=1 is equivalent to inner product. >>> x = paddle.arange(10, dtype=data_type) >>> y = paddle.arange(10, dtype=data_type) >>> z1 = paddle.tensordot(x, y, axes=1) >>> z2 = paddle.dot(x, y) >>> print(z1) Tensor(shape=[], dtype=float64, place=Place(cpu), stop_gradient=True, 285.) >>> print(z2) Tensor(shape=[], dtype=float64, place=Place(cpu), stop_gradient=True, 285.) >>> # For two 2-d tensor x and y, the case axes=1 is equivalent to matrix multiplication. >>> x = paddle.arange(6, dtype=data_type).reshape([2, 3]) >>> y = paddle.arange(12, dtype=data_type).reshape([3, 4]) >>> z1 = paddle.tensordot(x, y, axes=1) >>> z2 = paddle.matmul(x, y) >>> print(z1) Tensor(shape=[2, 4], dtype=float64, place=Place(cpu), stop_gradient=True, [[20., 23., 26., 29.], [56., 68., 80., 92.]]) >>> print(z2) Tensor(shape=[2, 4], dtype=float64, place=Place(cpu), stop_gradient=True, [[20., 23., 26., 29.], [56., 68., 80., 92.]]) >>> # When axes is a 1-d int list, x and y will be contracted along the same given axes. >>> # Note that axes=[1, 2] is equivalent to axes=[[1, 2]], axes=[[1, 2], []], axes=[[1, 2], [1]], and axes=[[1, 2], [1, 2]]. >>> x = paddle.arange(24, dtype=data_type).reshape([2, 3, 4]) >>> y = paddle.arange(36, dtype=data_type).reshape([3, 3, 4]) >>> z = paddle.tensordot(x, y, axes=[1, 2]) >>> print(z) Tensor(shape=[2, 3], dtype=float64, place=Place(cpu), stop_gradient=True, [[506. , 1298., 2090.], [1298., 3818., 6338.]]) >>> # When axes is a list containing two 1-d int list, the first will be applied to x and the second to y. >>> x = paddle.arange(60, dtype=data_type).reshape([3, 4, 5]) >>> y = paddle.arange(24, dtype=data_type).reshape([4, 3, 2]) >>> z = paddle.tensordot(x, y, axes=([1, 0], [0, 1])) >>> print(z) Tensor(shape=[5, 2], dtype=float64, place=Place(cpu), stop_gradient=True, [[4400., 4730.], [4532., 4874.], [4664., 5018.], [4796., 5162.], [4928., 5306.]]) >>> # Thanks to the support of axes expansion, axes=[[0, 1, 3, 4], [1, 0, 3, 4]] can be abbreviated as axes= [[0, 1, 3, 4], [1, 0]]. >>> x = paddle.arange(720, dtype=data_type).reshape([2, 3, 4, 5, 6]) >>> y = paddle.arange(720, dtype=data_type).reshape([3, 2, 4, 5, 6]) >>> z = paddle.tensordot(x, y, axes=[[0, 1, 3, 4], [1, 0]]) >>> print(z) Tensor(shape=[4, 4], dtype=float64, place=Place(cpu), stop_gradient=True, [[23217330., 24915630., 26613930., 28312230.], [24915630., 26775930., 28636230., 30496530.], [26613930., 28636230., 30658530., 32680830.], [28312230., 30496530., 32680830., 34865130.]])
-
tile
(
repeat_times: TensorOrTensors | Sequence[int],
name: str | None = None
)
Tensor
tile¶
-
Construct a new Tensor by repeating
xthe number of times given byrepeat_times. After tiling, the value of the i’th dimension of the output is equal tox.shape[i]*repeat_times[i].Both the number of dimensions of
xand the number of elements inrepeat_timesshould be less than or equal to 6.- Parameters
-
x (Tensor) – The input tensor, its data type should be bool, float16, float32, float64, int32, int64, complex64 or complex128.
repeat_times (list|tuple|Tensor) – The number of repeating times. If repeat_times is a list or tuple, all its elements should be integers or 1-D Tensors with the data type int32. If repeat_times is a Tensor, it should be an 1-D Tensor with the data type int32.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
N-D Tensor. The data type is the same as
x. The size of the i-th dimension is equal tox[i] * repeat_times[i].
Examples
>>> import paddle >>> data = paddle.to_tensor([1, 2, 3], dtype='int32') >>> out = paddle.tile(data, repeat_times=[2, 1]) >>> print(out) Tensor(shape=[2, 3], dtype=int32, place=Place(cpu), stop_gradient=True, [[1, 2, 3], [1, 2, 3]]) >>> out = paddle.tile(data, repeat_times=(2, 2)) >>> print(out) Tensor(shape=[2, 6], dtype=int32, place=Place(cpu), stop_gradient=True, [[1, 2, 3, 1, 2, 3], [1, 2, 3, 1, 2, 3]]) >>> repeat_times = paddle.to_tensor([1, 2], dtype='int32') >>> out = paddle.tile(data, repeat_times=repeat_times) >>> print(out) Tensor(shape=[1, 6], dtype=int32, place=Place(cpu), stop_gradient=True, [[1, 2, 3, 1, 2, 3]])
-
top_p_sampling
(
ps: Tensor,
threshold: Tensor | None = None,
topp_seed: Tensor | None = None,
seed: int = -1,
k: int = 0,
mode: Literal['truncated', 'non-truncated'] = 'truncated',
return_top: bool = False,
name: str | None = None
)
tuple[Tensor, Tensor]
top_p_sampling¶
-
Get the TopP scores and ids.
- Parameters
-
x (Tensor) – An input 2-D Tensor with type float32, float16 and bfloat16.
ps (Tensor) – A 1-D Tensor with type float32, float16 and bfloat16, used to specify the top_p corresponding to each query.
threshold (Tensor|None, optional) – A 1-D Tensor with type float32, float16 and bfloat16, used to avoid sampling low score tokens.
topp_seed (Tensor|None, optional) – A 1-D Tensor with type int64, used to specify the random seed for each query.
seed (int, optional) – the random seed. Default is -1,
k (int) – the number of top_k scores/ids to be returned. Default is 0.
mode (str) – The mode to choose sampling strategy. If the mode is truncated, sampling will truncate the probability at top_p_value. If the mode is non-truncated, it will not be truncated. Default is truncated.
return_top (bool) – Whether to return the top_k scores and ids. Default is False.
name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Returns
-
tuple(Tensor), return the values and indices. The value data type is the same as the input x. The indices data type is int64.
Examples
>>> >>> import paddle >>> paddle.device.set_device('gpu') >>> paddle.seed(2023) >>> x = paddle.randn([2,3]) >>> print(x) Tensor(shape=[2, 3], dtype=float32, place=Place(gpu:0), stop_gradient=True, [[-0.32012719, -0.07942779, 0.26011357], [ 0.79003978, -0.39958701, 1.42184138]]) >>> paddle.seed(2023) >>> ps = paddle.randn([2]) >>> print(ps) Tensor(shape=[2], dtype=float32, place=Place(gpu:0), stop_gradient=True, [-0.32012719, -0.07942779]) >>> value, index = paddle.tensor.top_p_sampling(x, ps) >>> print(value) Tensor(shape=[2, 1], dtype=float32, place=Place(gpu:0), stop_gradient=True, [[0.26011357], [1.42184138]]) >>> print(index) Tensor(shape=[2, 1], dtype=int64, place=Place(gpu:0), stop_gradient=True, [[2], [2]])
-
topk
(
k: int | Tensor,
axis: int | None = None,
largest: bool = True,
sorted: bool = True,
name: str | None = None,
*,
out: tuple[Tensor, Tensor] | None = None
)
TopKRetType
topk¶
-
Return values and indices of the k largest or smallest at the optional axis. If the input is a 1-D Tensor, finds the k largest or smallest values and indices. If the input is a Tensor with higher rank, this operator computes the top k values and indices along the
axis.- Parameters
-
x (Tensor) – Tensor, an input N-D Tensor with type float32, float64, int32, int64.
k (int, Tensor) – The number of top elements to look for along the axis.
axis (int|None, optional) – Axis to compute indices along. The effective range is [-R, R), where R is x.ndim. when axis < 0, it works the same way as axis + R. Default is -1.
largest (bool, optional) – largest is a flag, if set to true, algorithm will sort by descending order, otherwise sort by ascending order. Default is True.
sorted (bool, optional) – controls whether to return the elements in sorted order, default value is True.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
tuple(Tensor), return the values and indices. The value data type is the same as the input x. The indices data type is int64.
Examples
>>> import paddle >>> data_1 = paddle.to_tensor([1, 4, 5, 7]) >>> value_1, indices_1 = paddle.topk(data_1, k=1) >>> print(value_1) Tensor(shape=[1], dtype=int64, place=Place(cpu), stop_gradient=True, [7]) >>> print(indices_1) Tensor(shape=[1], dtype=int64, place=Place(cpu), stop_gradient=True, [3]) >>> data_2 = paddle.to_tensor([[1, 4, 5, 7], [2, 6, 2, 5]]) >>> value_2, indices_2 = paddle.topk(data_2, k=1) >>> print(value_2) Tensor(shape=[2, 1], dtype=int64, place=Place(cpu), stop_gradient=True, [[7], [6]]) >>> print(indices_2) Tensor(shape=[2, 1], dtype=int64, place=Place(cpu), stop_gradient=True, [[3], [1]]) >>> value_3, indices_3 = paddle.topk(data_2, k=1, axis=-1) >>> print(value_3) Tensor(shape=[2, 1], dtype=int64, place=Place(cpu), stop_gradient=True, [[7], [6]]) >>> print(indices_3) Tensor(shape=[2, 1], dtype=int64, place=Place(cpu), stop_gradient=True, [[3], [1]]) >>> value_4, indices_4 = paddle.topk(data_2, k=1, axis=0) >>> print(value_4) Tensor(shape=[1, 4], dtype=int64, place=Place(cpu), stop_gradient=True, [[2, 6, 5, 7]]) >>> print(indices_4) Tensor(shape=[1, 4], dtype=int64, place=Place(cpu), stop_gradient=True, [[1, 1, 0, 0]])
-
trace
(
offset: int = 0,
axis1: int = 0,
axis2: int = 1,
name: str | None = None
)
Tensor
trace¶
-
Computes the sum along diagonals of the input tensor x.
If
xis 2D, returns the sum of diagonal.If
xhas larger dimensions, then returns an tensor of diagonals sum, diagonals be taken from the 2D planes specified by axis1 and axis2. By default, the 2D planes formed by the first and second axes of the input tensor x.The argument
offsetdetermines where diagonals are taken from input tensor x:If offset = 0, it is the main diagonal.
If offset > 0, it is above the main diagonal.
If offset < 0, it is below the main diagonal.
Note that if offset is out of input’s shape indicated by axis1 and axis2, 0 will be returned.
- Parameters
-
x (Tensor) – The input tensor x. Must be at least 2-dimensional. The input data type should be float16, float32, float64, int32, int64.
offset (int, optional) – Which diagonals in input tensor x will be taken. Default: 0 (main diagonals).
axis1 (int, optional) – The first axis with respect to take diagonal. Default: 0.
axis2 (int, optional) – The second axis with respect to take diagonal. Default: 1.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
the output data type is the same as input data type.
- Return type
-
Tensor
Examples
>>> import paddle >>> case1 = paddle.randn([2, 3]) >>> case2 = paddle.randn([3, 10, 10]) >>> case3 = paddle.randn([3, 10, 5, 10]) >>> data1 = paddle.trace(case1) >>> data1.shape [] >>> data2 = paddle.trace(case2, offset=1, axis1=1, axis2=2) >>> data2.shape [3] >>> data3 = paddle.trace(case3, offset=-3, axis1=1, axis2=-1) >>> data3.shape [3, 5]
-
transpose
(
perm: Sequence[int],
name: str | None = None
)
Tensor
transpose¶
-
Permute the data dimensions of input according to perm.
The i-th dimension of the returned tensor will correspond to the perm[i]-th dimension of input.
Note
Alias Support: The parameter name
inputcan be used as an alias forx, anddim0&dim1can replaceperm. For example,transpose(input=x, dim0=0, dim1=1)is equivalent totranspose(x=x, perm=[1, 0, 2]).- Parameters
-
x (Tensor) – The input Tensor. It is a N-D Tensor of data types bool, float16, bfloat16, float32, float64, int8, int16, int32, int64, uint8, uint16, complex64, complex128. alias:
input.perm (list|tuple) – Permute the input according to the data of perm.
name (str|None, optional) – The name of this layer. For more information, please refer to api_guide_Name. Default is None.
- Returns
-
A transposed n-D Tensor, with data type being bool, float32, float64, int32, int64.
- Return type
-
Tensor
Examples
# The following codes in this code block are pseudocode, designed to show the execution logic and results of the function. x = to_tensor([[[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]] [[13 14 15 16] [17 18 19 20] [21 22 23 24]]]) shape(x): return [2,3,4] # Example 1 perm0 = [1,0,2] y_perm0 = transpose(x, perm0) # Permute x by perm0 # dim:0 of y_perm0 is dim:1 of x # dim:1 of y_perm0 is dim:0 of x # dim:2 of y_perm0 is dim:2 of x # The above two lines can also be understood as exchanging the zeroth and first dimensions of x y_perm0.data = [[[ 1 2 3 4] [13 14 15 16]] [[ 5 6 7 8] [17 18 19 20]] [[ 9 10 11 12] [21 22 23 24]]] shape(y_perm0): return [3,2,4] # Example 2 perm1 = [2,1,0] y_perm1 = transpose(x, perm1) # Permute x by perm1 # dim:0 of y_perm1 is dim:2 of x # dim:1 of y_perm1 is dim:1 of x # dim:2 of y_perm1 is dim:0 of x # The above two lines can also be understood as exchanging the zeroth and second dimensions of x y_perm1.data = [[[ 1 13] [ 5 17] [ 9 21]] [[ 2 14] [ 6 18] [10 22]] [[ 3 15] [ 7 19] [11 23]] [[ 4 16] [ 8 20] [12 24]]] shape(y_perm1): return [4,3,2]Examples
>>> import paddle >>> x = paddle.randn([2, 3, 4]) >>> x_transposed = paddle.transpose(x, perm=[1, 0, 2]) >>> print(x_transposed.shape) [3, 2, 4]
-
transpose_
(
perm,
name=None
)
transpose_¶
-
Inplace version of
transposeAPI, the output Tensor will be inplaced with inputx. Please refer to api_paddle_transpose.
-
trapezoid
(
x: Tensor | None = None,
dx: float | None = None,
axis: int = -1,
name: str | None = None
)
Tensor
trapezoid¶
-
Integrate along the given axis using the composite trapezoidal rule. Use the sum method.
- Parameters
-
y (Tensor) – Input tensor to integrate. It’s data type should be float16, float32, float64.
x (Tensor|None, optional) – The sample points corresponding to the
yvalues, the same type asy. It is known that the size ofyis [d_1, d_2, … , d_n] and \(axis=k\), then the size ofxcan only be [d_k] or [d_1, d_2, … , d_n ]. Ifxis None, the sample points are assumed to be evenly spaceddxapart. The default is None.dx (float|None, optional) – The spacing between sample points when
xis None. If neitherxnordxis provided then the default is \(dx = 1\).axis (int, optional) – The axis along which to integrate. The default is -1.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, Definite integral of
yis N-D tensor as approximated along a single axis by the trapezoidal rule. Ifyis a 1D tensor, then the result is a float. If N is greater than 1, then the result is an (N-1)-D tensor.
Examples
>>> import paddle >>> y = paddle.to_tensor([4, 5, 6], dtype='float32') >>> paddle.trapezoid(y) Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 10.) >>> paddle.trapezoid(y, dx=2.) Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 20.) >>> y = paddle.to_tensor([4, 5, 6], dtype='float32') >>> x = paddle.to_tensor([1, 2, 3], dtype='float32') >>> paddle.trapezoid(y, x) Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 10.) >>> y = paddle.to_tensor([1, 2, 3], dtype='float64') >>> x = paddle.to_tensor([8, 6, 4], dtype='float64') >>> paddle.trapezoid(y, x) Tensor(shape=[], dtype=float64, place=Place(cpu), stop_gradient=True, -8.) >>> y = paddle.arange(6).reshape((2, 3)).astype('float32') >>> paddle.trapezoid(y, axis=0) Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True, [1.50000000, 2.50000000, 3.50000000]) >>> paddle.trapezoid(y, axis=1) Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True, [2., 8.])
-
tril
(
)
tril¶
-
C++ interface function for tril.
-
tril_
(
diagonal: int = 0,
name: str | None = None
)
paddle.Tensor | None
tril_¶
-
Inplace version of
trilAPI, the output Tensor will be inplaced with inputx. Please refer to tril.
-
triu
(
)
triu¶
-
C++ interface function for triu.
-
triu_
(
diagonal: int = 0,
name: str | None = None
)
paddle.Tensor | None
triu_¶
-
Inplace version of
triuAPI, the output Tensor will be inplaced with inputx. Please refer to triu.
-
true_divide
(
other: Tensor,
*,
out: Tensor | None = None
)
Tensor
true_divide¶
-
Alias for paddle.divide with rounding_mode=None. Please refer to api_paddle_divide.
-
trunc
(
name: str | None = None
)
Tensor
trunc¶
-
This API is used to returns a new tensor with the truncated integer values of input.
- Parameters
-
input (Tensor) – The input tensor, it’s data type should be int32, int64, float32, float64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
The output Tensor of trunc.
- Return type
-
Tensor
Examples
>>> import paddle >>> input = paddle.to_tensor([[0.1, 1.5], [-0.2, -2.4]], 'float32') >>> output = paddle.trunc(input) >>> output Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True, [[ 0., 1.], [-0., -2.]])
-
trunc_
(
name: str | None = None
)
Tensor
trunc_¶
-
Inplace version of
truncAPI, the output Tensor will be inplaced with inputx. Please refer to trunc.
-
unbind
(
axis: int = 0
)
list[Tensor]
unbind¶
-
Removes a tensor dimension, then split the input tensor into multiple sub-Tensors.
- Parameters
-
input (Tensor) – The input variable which is an N-D Tensor, data type being bool, float16, float32, float64, int32, int64, complex64 or complex128.
axis (int, optional) – A 0-D Tensor with shape [] and type is
int32|int64. The dimension along which to unbind. If \(axis < 0\), the dimension to unbind along is \(rank(input) + axis\). Default is 0.
- Returns
-
list(Tensor), The list of segmented Tensor variables.
Examples
>>> import paddle >>> # input is a Tensor which shape is [3, 4, 5] >>> input = paddle.rand([3, 4, 5]) >>> [x0, x1, x2] = paddle.unbind(input, axis=0) >>> # x0.shape [4, 5] >>> # x1.shape [4, 5] >>> # x2.shape [4, 5] >>> [x0, x1, x2, x3] = paddle.unbind(input, axis=1) >>> # x0.shape [3, 5] >>> # x1.shape [3, 5] >>> # x2.shape [3, 5] >>> # x3.shape [3, 5]
-
unflatten
(
axis: int,
shape: ShapeLike,
name: str | None = None
)
Tensor
unflatten¶
-
Expand a certain dimension of the input x Tensor into a desired shape.
The figure below shows the shape of a [2, 6] Tensor after applying
unflatten(X, axis=1, shape=(2, 3)), with data ranging from 0 to 11 in sequence.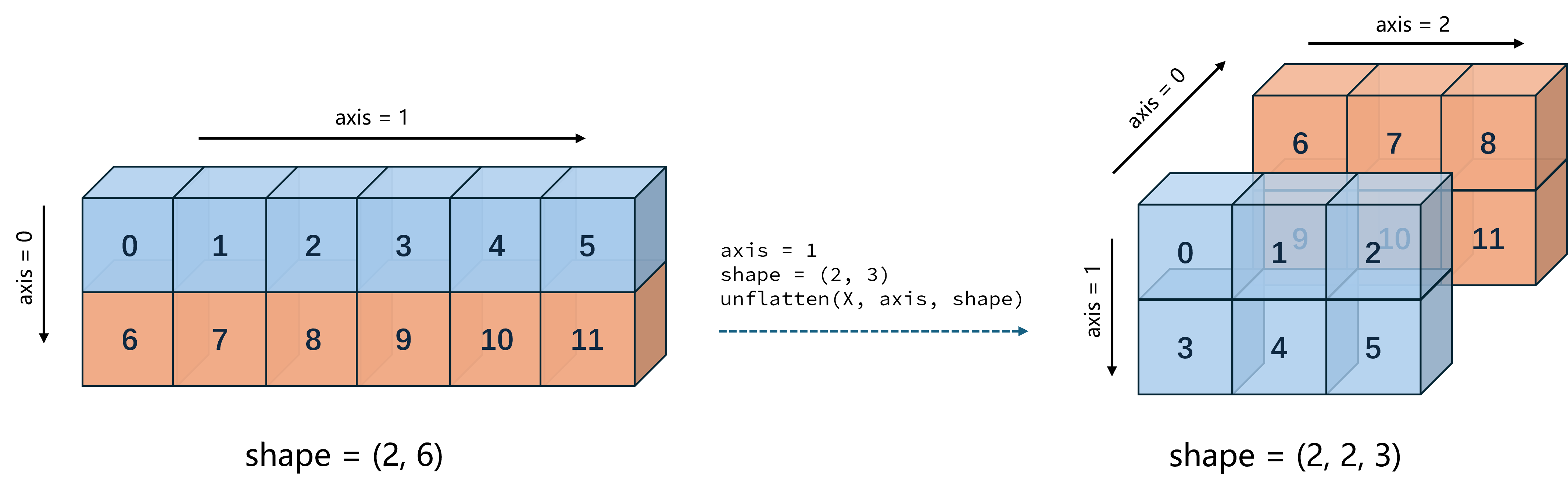
- Parameters
-
x (Tensor) – An N-D Tensor. The data type is float16, float32, float64, int16, int32, int64, bool, uint16.
axis (int) –
axisto be unflattened, specified as an index into x.shape.shape (list|tuple|Tensor) – Unflatten
shapeon the specifiedaxis. At most one dimension of the targetshapecan be -1. If the inputshapedoes not contain -1 , the product of all elements inshapeshould be equal tox.shape[axis]. The data type is int . Ifshapeis a list or tuple, the elements of it should be integers or Tensors with shape []. Ifshapeis an Tensor, it should be an 1-D Tensor.name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Returns
-
Tensor, return the unflatten tensor of
x.
Examples
>>> import paddle >>> x = paddle.randn(shape=[4, 6, 8]) >>> shape = [2, 3] >>> axis = 1 >>> res = paddle.unflatten(x, axis, shape) >>> print(res.shape) [4, 2, 3, 8] >>> x = paddle.randn(shape=[4, 6, 8]) >>> shape = (-1, 2) >>> axis = -1 >>> res = paddle.unflatten(x, axis, shape) >>> print(res.shape) [4, 6, 4, 2] >>> x = paddle.randn(shape=[4, 6, 8]) >>> shape = paddle.to_tensor([2, 2]) >>> axis = 0 >>> res = paddle.unflatten(x, axis, shape) >>> print(res.shape) [2, 2, 6, 8]
-
unfold
(
axis: int,
size: int,
step: int,
name: str | None = None
)
Tensor
unfold¶
-
View x with specified shape, stride and offset, which contains all slices of size from x in the dimension axis.
Note that the output Tensor will share data with origin Tensor and doesn’t have a Tensor copy in
dygraphmode.- Parameters
-
x (Tensor) – An N-D Tensor. The data type is
float32,float64,int32,int64orboolaxis (int) – The axis along which the input is unfolded.
size (int) – The size of each slice that is unfolded.
step (int) – The step between each slice.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, A unfold Tensor with the same data type as
x.
Examples
>>> import paddle >>> paddle.base.set_flags({"FLAGS_use_stride_kernel": True}) >>> x = paddle.arange(9, dtype="float64") >>> out = paddle.unfold(x, 0, 2, 4) >>> print(out) Tensor(shape=[2, 2], dtype=float64, place=Place(cpu), stop_gradient=True, [[0., 1.], [4., 5.]])
-
uniform_
(
min: float = -1.0,
max: float = 1.0,
seed: int = 0,
name: str | None = None
)
Tensor
uniform_¶
-
This is the inplace version of OP
uniform, which returns a Tensor filled with random values sampled from a uniform distribution. The output Tensor will be inplaced with inputx. Please refer to uniform.- Parameters
-
x (Tensor) – The input tensor to be filled with random values.
min (float|int, optional) – The lower bound on the range of random values to generate,
minis included in the range. Default is -1.0.max (float|int, optional) – The upper bound on the range of random values to generate,
maxis excluded in the range. Default is 1.0.seed (int, optional) – Random seed used for generating samples. If seed is 0, it will use the seed of the global default generator (which can be set by paddle.seed). Note that if seed is not 0, this operator will always generate the same random numbers every time. Default is 0.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name.
- Returns
-
Tensor, The input tensor x filled with random values sampled from a uniform distribution in the range [
min,max).
Examples
>>> import paddle >>> # example: >>> x = paddle.ones(shape=[3, 4]) >>> x.uniform_() >>> Tensor(shape=[3, 4], dtype=float32, place=Place(cpu), stop_gradient=True, [[-0.50484276, 0.49580324, 0.33357990, -0.93924278], [ 0.39779735, 0.87677515, -0.24377221, 0.06212139], [-0.92499518, -0.96244860, 0.79210341, -0.78228098]]) >>>
-
unique
(
return_index=False,
return_inverse=False,
return_counts=False,
axis=None,
dtype='int64',
name=None
)
unique¶
-
Returns the unique elements of x in ascending order.
- Parameters
-
x (Tensor) – The input tensor, it’s data type should be float32, float64, int32, int64.
return_index (bool, optional) – If True, also return the indices of the input tensor that result in the unique Tensor.
return_inverse (bool, optional) – If True, also return the indices for where elements in the original input ended up in the returned unique tensor.
return_counts (bool, optional) – If True, also return the counts for each unique element.
axis (int, optional) – The axis to apply unique. If None, the input will be flattened. Default: None.
dtype (np.dtype|str, optional) – The date type of indices or inverse tensor: int32 or int64. Default: int64.
name (str|None, optional) – Name for the operation. For more information, please refer to api_guide_Name. Default: None.
- Returns
-
- tuple (out, indices, inverse, counts). out is the unique tensor for x. indices is
-
provided only if return_index is True. inverse is provided only if return_inverse is True. counts is provided only if return_counts is True.
Examples
>>> import paddle >>> x = paddle.to_tensor([2, 3, 3, 1, 5, 3]) >>> unique = paddle.unique(x) >>> print(unique) Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True, [1, 2, 3, 5]) >>> _, indices, inverse, counts = paddle.unique(x, return_index=True, return_inverse=True, return_counts=True) >>> print(indices) Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True, [3, 0, 1, 4]) >>> print(inverse) Tensor(shape=[6], dtype=int64, place=Place(cpu), stop_gradient=True, [1, 2, 2, 0, 3, 2]) >>> print(counts) Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True, [1, 1, 3, 1]) >>> x = paddle.to_tensor([[2, 1, 3], [3, 0, 1], [2, 1, 3]]) >>> unique = paddle.unique(x) >>> print(unique) Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True, [0, 1, 2, 3]) >>> unique = paddle.unique(x, axis=0) >>> print(unique) Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[2, 1, 3], [3, 0, 1]])
-
unique_consecutive
(
return_inverse: bool = False,
return_counts: bool = False,
axis: int | None = None,
dtype: DTypeLike = 'int64',
name: str | None = None
)
tuple[Tensor, Tensor, Tensor]
unique_consecutive¶
-
Eliminates all but the first element from every consecutive group of equivalent elements.
Note
This function is different from unique in the sense that this function only eliminates consecutive duplicate values. This semantics is similar to unique in C++.
Note
Alias Support: The parameter name
inputcan be used as an alias forx, anddimcan be used as an alias foraxis. For example,unique_consecutive(input=tensor_x, dim=1, ...)is equivalent tounique_consecutive(x=tensor_x, axis=1, ...).- Parameters
-
x (Tensor) – the input tensor, it’s data type should be float32, float64, int32, int64. alias:
input.return_inverse (bool, optional) – If True, also return the indices for where elements in the original input ended up in the returned unique consecutive tensor. Default is False.
return_counts (bool, optional) – If True, also return the counts for each unique consecutive element. Default is False.
axis (int, optional) – The axis to apply unique consecutive. If None, the input will be flattened. Default is None. alias:
dim.dtype (np.dtype|str, optional) – The data type inverse tensor: int32 or int64. Default: int64.
name (str|None, optional) – Name for the operation. For more information, please refer to api_guide_Name. Default is None.
- Returns
-
out (Tensor), the unique consecutive tensor for x.
-
- inverse (Tensor), the element of the input tensor corresponds to
-
the index of the elements in the unique consecutive tensor for x. inverse is provided only if return_inverse is True.
-
- counts (Tensor), the counts of the every unique consecutive element in the input tensor.
-
counts is provided only if return_counts is True.
Examples
>>> import paddle >>> x = paddle.to_tensor([1, 1, 2, 2, 3, 1, 1, 2]) >>> output = paddle.unique_consecutive(x) # >>> print(output) Tensor(shape=[5], dtype=int64, place=Place(cpu), stop_gradient=True, [1, 2, 3, 1, 2]) >>> _, inverse, counts = paddle.unique_consecutive(x, return_inverse=True, return_counts=True) >>> print(inverse) Tensor(shape=[8], dtype=int64, place=Place(cpu), stop_gradient=True, [0, 0, 1, 1, 2, 3, 3, 4]) >>> print(counts) Tensor(shape=[5], dtype=int64, place=Place(cpu), stop_gradient=True, [2, 2, 1, 2, 1]) >>> x = paddle.to_tensor([[2, 1, 3], [3, 0, 1], [2, 1, 3], [2, 1, 3]]) >>> output = paddle.unique_consecutive(x, axis=0) # >>> print(output) Tensor(shape=[3, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[2, 1, 3], [3, 0, 1], [2, 1, 3]]) >>> x = paddle.to_tensor([[2, 1, 3], [3, 0, 1], [2, 1, 3], [2, 1, 3]]) >>> output = paddle.unique_consecutive(x, axis=0) # >>> print(output) Tensor(shape=[3, 3], dtype=int64, place=Place(cpu), stop_gradient=True, [[2, 1, 3], [3, 0, 1], [2, 1, 3]])
-
unsqueeze
(
axis: int | Sequence[Tensor | int] | Tensor,
name: str | None = None
)
Tensor
unsqueeze¶
-
Insert single-dimensional entries to the shape of input Tensor
x. Takes one required argument axis, a dimension or list of dimensions that will be inserted. Dimension indices in axis are as seen in the output tensor.Note that the output Tensor will share data with origin Tensor and doesn’t have a Tensor copy in
dygraphmode. If you want to use the Tensor copy version, please use Tensor.clone likeunsqueeze_clone_x = x.unsqueeze(-1).clone().Note
Alias Support: The parameter name
inputcan be used as an alias forx, anddimcan be used as an alias foraxis. For example,unsqueeze(input=tensor_x, dim=1)is equivalent tounsqueeze(x=tensor_x, axis=1).- Parameters
-
x (Tensor) – The input Tensor to be unsqueezed. Supported data type: bfloat16, float16, float32, float64, bool, int8, int32, int64. alias:
input.axis (int|list|tuple|Tensor) –
-
Indicates the dimensions to be inserted. The data type is
int32. -
If
axisis a list or tuple, each element of it should be integer or 0-D Tensor with shape []. Ifaxisis a Tensor, it should be an 1-D Tensor . Ifaxisis negative,axis = axis + ndim(x) + 1.
alias:
dim.-
Indicates the dimensions to be inserted. The data type is
name (str|None, optional) – Name for this layer. Please refer to api_guide_Name, Default None.
- Returns
-
Tensor, Unsqueezed Tensor with the same data type as input Tensor.
Examples
>>> import paddle >>> x = paddle.rand([5, 10]) >>> print(x.shape) [5, 10] >>> out1 = paddle.unsqueeze(x, axis=0) >>> print(out1.shape) [1, 5, 10] >>> out2 = paddle.unsqueeze(x, axis=[0, 2]) >>> print(out2.shape) [1, 5, 1, 10] >>> axis = paddle.to_tensor([0, 1, 2]) >>> out3 = paddle.unsqueeze(x, axis=axis) >>> print(out3.shape) [1, 1, 1, 5, 10] >>> # out1, out2, out3 share data with x in dygraph mode >>> x[0, 0] = 10. >>> print(out1[0, 0, 0]) Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 10.) >>> print(out2[0, 0, 0, 0]) Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 10.) >>> print(out3[0, 0, 0, 0, 0]) Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 10.)
-
unsqueeze_
(
axis: int | Sequence[int] | Tensor,
name: str | None = None
)
Tensor
unsqueeze_¶
-
Inplace version of
unsqueezeAPI, the output Tensor will be inplaced with inputx. Please refer to api_paddle_tensor_unsqueeze.
-
unstack
(
axis: int = 0,
num: int | None = None
)
list[Tensor]
unstack¶
-
This layer unstacks input Tensor
xinto several Tensors alongaxis.If
axis< 0, it would be replaced withaxis+rank(x). Ifnumis None, it would be inferred fromx.shape[axis], and ifx.shape[axis]<= 0 or is unknown,ValueErroris raised.- Parameters
-
x (Tensor) – Input Tensor. It is a N-D Tensors of data types float32, float64, int32, int64, complex64, complex128.
axis (int, optional) – The axis along which the input is unstacked.
num (int|None, optional) – The number of output variables.
- Returns
-
list(Tensor), The unstacked Tensors list. The list elements are N-D Tensors of data types float32, float64, int32, int64, complex64, complex128.
Examples
>>> import paddle >>> x = paddle.ones(name='x', shape=[2, 3, 5], dtype='float32') # create a tensor with shape=[2, 3, 5] >>> y = paddle.unstack(x, axis=1) # unstack with second axis, which results 3 tensors with shape=[2, 5]
-
vander
(
n: int | None = None,
increasing: bool = False,
name: str | None = None
)
Tensor
vander¶
-
Generate a Vandermonde matrix.
The columns of the output matrix are powers of the input vector. Order of the powers is determined by the increasing Boolean parameter. Specifically, when the increment is “false”, the ith output column is a step-up in the order of the elements of the input vector to the N - i - 1 power. Such a matrix with a geometric progression in each row is named after Alexandre-Theophile Vandermonde.
- Parameters
-
x (Tensor) – The input tensor, it must be 1-D Tensor, and it’s data type should be [‘complex64’, ‘complex128’, ‘float32’, ‘float64’, ‘int32’, ‘int64’].
n (int|None) – Number of columns in the output. If n is not specified, a square array is returned (n = len(x)).
increasing (bool) – Order of the powers of the columns. If True, the powers increase from left to right, if False (the default) they are reversed.
name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
- Returns
-
Tensor, A vandermonde matrix with shape (len(x), N). If increasing is False, the first column is \(x^{(N-1)}\), the second \(x^{(N-2)}\) and so forth. If increasing is True, the columns are \(x^0\), \(x^1\), …, \(x^{(N-1)}\).
Examples
>>> import paddle >>> x = paddle.to_tensor([1., 2., 3.], dtype="float32") >>> out = paddle.vander(x) >>> out Tensor(shape=[3, 3], dtype=float32, place=Place(cpu), stop_gradient=True, [[1., 1., 1.], [4., 2., 1.], [9., 3., 1.]]) >>> out1 = paddle.vander(x,2) >>> out1 Tensor(shape=[3, 2], dtype=float32, place=Place(cpu), stop_gradient=True, [[1., 1.], [2., 1.], [3., 1.]]) >>> out2 = paddle.vander(x, increasing = True) >>> out2 Tensor(shape=[3, 3], dtype=float32, place=Place(cpu), stop_gradient=True, [[1., 1., 1.], [1., 2., 4.], [1., 3., 9.]]) >>> real = paddle.to_tensor([2., 4.]) >>> imag = paddle.to_tensor([1., 3.]) >>> complex = paddle.complex(real, imag) >>> out3 = paddle.vander(complex) >>> out3 Tensor(shape=[2, 2], dtype=complex64, place=Place(cpu), stop_gradient=True, [[(2+1j), (1+0j)], [(4+3j), (1+0j)]])
-
var
(
axis: int | Sequence[int] | None = None,
unbiased: bool | None = None,
keepdim: bool = False,
name: str | None = None,
*,
correction: float = 1,
out: Tensor | None = None
)
Tensor
var¶
-
Computes the variance of
xalongaxis.Note
Alias Support: The parameter name
inputcan be used as an alias forx, anddimcan be used as an alias foraxis. For example,var(input=tensor_x, dim=1, ...)is equivalent tovar(x=tensor_x, axis=1, ...).- Parameters
-
x (Tensor) – The input Tensor with data type float16, float32, float64. alias:
input.axis (int|list|tuple|None, optional) –
The axis along which to perform variance calculations.
axisshould be int, list(int) or tuple(int). alias:dim.If
axisis a list/tuple of dimension(s), variance is calculated along all element(s) ofaxis.axisor element(s) ofaxisshould be in range [-D, D), where D is the dimensions ofx.If
axisor element(s) ofaxisis less than 0, it works the same way as \(axis + D\) .If
axisis None, variance is calculated over all elements ofx. Default is None.
unbiased (bool, optional) – Whether to use the unbiased estimation. If
unbiasedis True, the divisor used in the computation is \(N - 1\), where \(N\) represents the number of elements alongaxis, otherwise the divisor is \(N\). Default is True.keep_dim (bool, optional) – Whether to reserve the reduced dimension in the output Tensor. The result tensor will have one fewer dimension than the input unless keep_dim is true. Default is False.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
correction (int|float, optional) – Difference between the sample size and sample degrees of freedom. Defaults to 1 (Bessel’s correction). If unbiased is specified, this parameter is ignored.
out (Tensor|None, optional) – Output tensor. Default is None.
- Returns
-
Tensor, results of variance along
axisofx, with the same data type asx.
Examples
>>> import paddle >>> x = paddle.to_tensor([[1.0, 2.0, 3.0], [1.0, 4.0, 5.0]]) >>> out1 = paddle.var(x) >>> print(out1.numpy()) 2.6666667 >>> out2 = paddle.var(x, axis=1) >>> print(out2.numpy()) [1. 4.3333335]
-
view
(
shape_or_dtype: Sequence[int] | DTypeLike,
name: str | None = None
)
Tensor
view¶
-
View x with specified shape or dtype.
Note that the output Tensor will share data with origin Tensor and doesn’t have a Tensor copy in
dygraphmode.Note
Alias Support: The parameter name
sizeanddtypecan be used as an alias forshape_or_dtype.shape_or_dtypecan be a variable number of arguments. For example:tensor_x.view(dtype=paddle.float32)tensor_x.view(size=[-1, 1, 3])tensor_x.view(-1, 1, 3)- Parameters
-
x (Tensor) – An N-D Tensor. The data type is
float32,float64,int32,int64orboolshape_or_dtype (list|tuple|np.dtype|str|VarType|variable number of arguments) – Define the target shape or dtype. If list or tuple, shape_or_dtype represents shape, each element of it should be integer. If np.dtype or str or VarType, shape_or_dtype represents dtype, it can be bool, float16, float32, float64, int8, int32, int64, uint8.
shape_or_dtypecan be a variable number of arguments. alias:sizeordtype.name (str, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, A viewed Tensor with the same data as
x.
Examples
>>> import paddle >>> paddle.base.set_flags({"FLAGS_use_stride_kernel": True}) >>> x = paddle.rand([2, 4, 6], dtype="float32") >>> out = paddle.view(x, [8, 6]) >>> print(out.shape) [8, 6] >>> import paddle >>> paddle.base.set_flags({"FLAGS_use_stride_kernel": True}) >>> x = paddle.rand([2, 4, 6], dtype="float32") >>> out = paddle.view(x, "uint8") >>> print(out.shape) [2, 4, 24] >>> import paddle >>> paddle.base.set_flags({"FLAGS_use_stride_kernel": True}) >>> x = paddle.rand([2, 4, 6], dtype="float32") >>> out = paddle.view(x, [8, -1]) >>> print(out.shape) [8, 6] >>> import paddle >>> paddle.base.set_flags({"FLAGS_use_stride_kernel": True}) >>> x = paddle.rand([2, 4, 6], dtype="float32") >>> out = paddle.view(x, paddle.uint8) >>> print(out.shape) [2, 4, 24]
-
view_as
(
other: Tensor,
name: str | None = None
)
Tensor
view_as¶
-
View x with other’s shape.
Note that the output Tensor will share data with origin Tensor and doesn’t have a Tensor copy in
dygraphmode.The following figure shows a view_as operation - a three-dimensional tensor with a shape of [2, 4, 6] is transformed into a two-dimensional tensor with a shape of [8, 6] through the view_as operation. We can clearly see the corresponding relationship between the elements before and after the transformation.
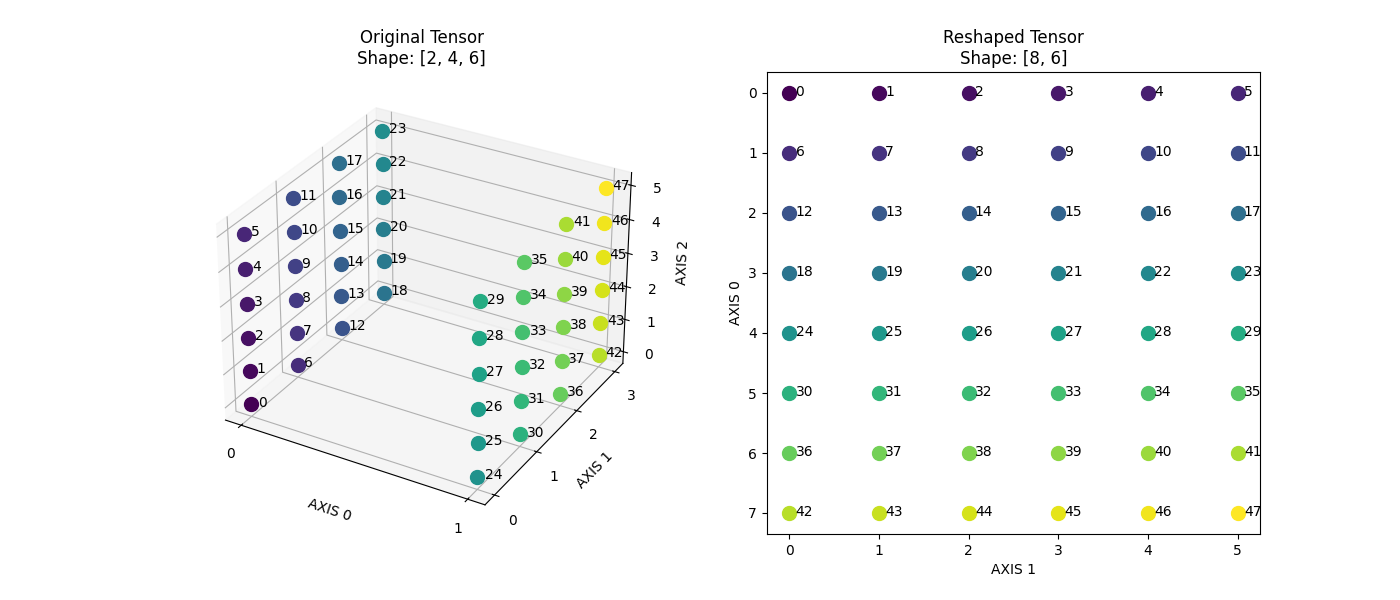
- Parameters
-
x (Tensor) – An N-D Tensor. The data type is
float32,float64,int32,int64orboolother (Tensor) – The result tensor has the same size as other.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to api_guide_Name.
- Returns
-
Tensor, A viewed Tensor with the same shape as
other.
Examples
>>> import paddle >>> paddle.base.set_flags({"FLAGS_use_stride_kernel": True}) >>> x = paddle.rand([2, 4, 6], dtype="float32") >>> y = paddle.rand([8, 6], dtype="float32") >>> out = paddle.view_as(x, y) >>> print(out.shape) [8, 6]
-
view_as_complex
(
)
Tensor
view_as_complex¶
-
Return a complex tensor that is a view of the input real tensor .
The data type of the input tensor is ‘float32’ or ‘float64’, and the data type of the returned tensor is ‘complex64’ or ‘complex128’, respectively.
The shape of the input tensor is
(* ,2), (*means arbitrary shape), i.e. the size of the last axis should be 2, which represent the real and imag part of a complex number. The shape of the returned tensor is(*,).The complex tensor is a view of the input real tensor, meaning that it shares the same memory with real tensor.
The image below demonstrates the case that a real 3D-tensor with shape [2, 3, 2] is transformed into a complex 2D-tensor with shape [2, 3].

- Parameters
-
input (Tensor) – The input tensor. Data type is ‘float32’ or ‘float64’.
- Returns
-
Tensor, The output. Data type is ‘complex64’ or ‘complex128’, sharing the same memory with input.
Examples
>>> import paddle >>> x = paddle.arange(12, dtype=paddle.float32).reshape([2, 3, 2]) >>> y = paddle.as_complex(x) >>> print(y) Tensor(shape=[2, 3], dtype=complex64, place=Place(cpu), stop_gradient=True, [[1j , (2+3j) , (4+5j) ], [(6+7j) , (8+9j) , (10+11j)]])
-
view_as_real
(
)
Tensor
view_as_real¶
-
Return a real tensor that is a view of the input complex tensor.
The data type of the input tensor is ‘complex64’ or ‘complex128’, and the data type of the returned tensor is ‘float32’ or ‘float64’, respectively.
When the shape of the input tensor is
(*, ), (*means arbitrary shape), the shape of the output tensor is(*, 2), i.e. the shape of the output is the shape of the input appended by an extra2.The real tensor is a view of the input complex tensor, meaning that it shares the same memory with complex tensor.
- Parameters
-
input (Tensor) – The input tensor. Data type is ‘complex64’ or ‘complex128’.
- Returns
-
Tensor, The output. Data type is ‘float32’ or ‘float64’, sharing the same memory with input.
Examples
>>> import paddle >>> x = paddle.arange(12, dtype=paddle.float32).reshape([2, 3, 2]) >>> y = paddle.as_complex(x) >>> z = paddle.as_real(y) >>> print(z) Tensor(shape=[2, 3, 2], dtype=float32, place=Place(cpu), stop_gradient=True, [[[0. , 1. ], [2. , 3. ], [4. , 5. ]], [[6. , 7. ], [8. , 9. ], [10., 11.]]])
-
vsplit
(
num_or_indices: int | Sequence[int],
name: str | None = None
)
list[Tensor]
vsplit¶
-
vsplitFull name Vertical Split, splits the input Tensor into multiple sub-Tensors along the vertical axis, which is equivalent topaddle.tensor_splitwithaxis=0.When the number of Tensor dimensions is equal to 2:
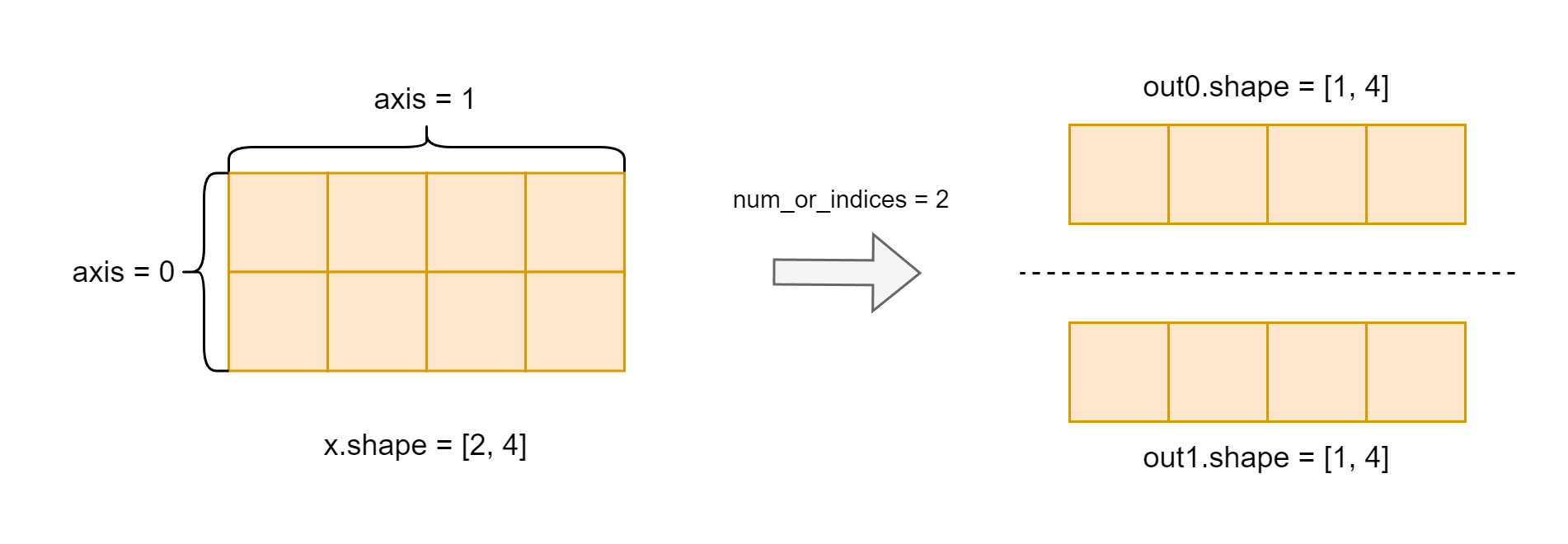
When the number of Tensor dimensions is greater than 2:

Note
Make sure that the number of Tensor dimensions transformed using
paddle.vsplitmust be not less than 2.- Parameters
-
x (Tensor) – A Tensor whose dimension must be greater than 1. The data type is bool, bfloat16, float16, float32, float64, uint8, int32 or int64.
num_or_indices (int|list|tuple) – If
num_or_indicesis an intn,xis split intonsections. Ifnum_or_indicesis a list or tuple of integer indices,xis split at each of the indices.name (str, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to api_guide_Name .
- Returns
-
list[Tensor], The list of segmented Tensors.
Examples
>>> import paddle >>> # x is a Tensor of shape [8, 6, 7] >>> x = paddle.rand([8, 6, 7]) >>> out0, out1 = paddle.vsplit(x, num_or_indices=2) >>> print(out0.shape) [4, 6, 7] >>> print(out1.shape) [4, 6, 7] >>> out0, out1, out2 = paddle.vsplit(x, num_or_indices=[1, 4]) >>> print(out0.shape) [1, 6, 7] >>> print(out1.shape) [3, 6, 7] >>> print(out2.shape) [4, 6, 7]
-
where
(
x: Tensor | float | None = None,
y: Tensor | float | None = None,
name: str | None = None,
*,
out: Tensor | None = None
)
Tensor
where¶
-
Return a Tensor of elements selected from either
xoryaccording to corresponding elements ofcondition. Concretely,\[\begin{split}out_i = \begin{cases} x_i, & \text{if} \ condition_i \ \text{is} \ True \\ y_i, & \text{if} \ condition_i \ \text{is} \ False \\ \end{cases}.\end{split}\]Notes
numpy.where(condition)is identical topaddle.nonzero(condition, as_tuple=True), please refer to nonzero.Note
Alias Support: The parameter name
inputcan be used as an alias forx, andothercan be used as an alias fory. For example,paddle.where(condition, input=x, other=y)can be written aspaddle.where(condition, x=x, y=y).- Parameters
-
condition (Tensor) – The condition to choose x or y. When True (nonzero), yield x, otherwise yield y, must have a dtype of bool if used as mask.
x (Tensor|scalar|None, optional) – A Tensor or scalar to choose when the condition is True with data type of bfloat16, float16, float32, float64, int32 or int64. Either both or neither of x and y should be given. alias:
input.y (Tensor|scalar|None, optional) – A Tensor or scalar to choose when the condition is False with data type of bfloat16, float16, float32, float64, int32 or int64. Either both or neither of x and y should be given. alias:
other.name (str|None, optional) – For details, please refer to api_guide_Name. Generally, no setting is required. Default: None.
out (Tensor|None, optional) – The output tensor. If set, the result will be stored to this tensor. Default is None.
- Returns
-
//www.paddlepaddle.org.cn/documentation/docs/en/develop/guides/advanced/auto_type_promotion_en.html#introduction-to-data-type-promotion>`_).
- Return type
-
Tensor, A Tensor with the same shape as
conditionand same data type asxandy. Ifxandyhave different data types, type promotion rules will be applied (see `Auto Type Promotion <https
Examples
>>> import paddle >>> x = paddle.to_tensor([0.9383, 0.1983, 3.2, 1.2]) >>> y = paddle.to_tensor([1.0, 1.0, 1.0, 1.0]) >>> out = paddle.where(x>1, x, y) >>> print(out) Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True, [1. , 1. , 3.20000005, 1.20000005]) >>> out = paddle.where(x>1) >>> print(out) (Tensor(shape=[2], dtype=int64, place=Place(cpu), stop_gradient=True, [2, 3]),)
-
detach
(
)